陕西省西安市莲湖区2022-2023学年高一下学期期末数学试题

试卷更新日期：2023-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. $(1 - 2 i) (1 - i) =$ （）

A、 $- 1 - 3 i$ B、 $3 - 3 i$ C、 $- 1 + i$ D、 $3 + i$

查看试题解析
2. 某超市到月末进行库存盘点，统计到玉米库存还剩四个品种，其中甜玉米42个，黑玉米7个，糯玉米56个，高油玉米35个．现用分层随机抽样抽取40个玉米作为内部嘉奖福利．则抽取的玉米中糯玉米的个数为（）

A、18 B、12 C、16 D、10

查看试题解析
3. 下列命题正确的是（）

A、任意四边形都可以确定唯一一个平面 B、若 $m ⊥ α$ ，则直线m与平面 $α$ 内的任意一条直线都垂直 C、若 $m / / α$ ，则直线m与平面 $α$ 内的任意一条直线都平行 D、若直线m上有无数个点不在平面 $α$ 内，则 $m / / α$

查看试题解析
4. 某倶乐部有5名登山爱好者，其中只有2人成功登顶珠穆朗玛峰．若从这5人中任选2人进行登山经验分享，则被选中的2人中恰有1人成功登顶珠穆朗玛峰的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{1}{5}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
5. 如图，一个水平放置的平面图形的直观图是直角 $△ O^{'} A B$ ，其中 $A B = \sqrt{10}$ ，则原图形的面积为（）

A、 $5 \sqrt{2}$ B、 $10 \sqrt{2}$ C、 $10 \sqrt{5}$ D、 $5 \sqrt{5}$

查看试题解析
6. 已知向量 $\vec{a}$ 的模长为2，向量 $\vec{b}$ 在向量 $\vec{a}$ 上的投影向量为 $\frac{1}{4} \vec{a}$ ，则 $\vec{a} \cdot \vec{b} =$ （）

A、8 B、4 C、2 D、1

查看试题解析
7. 已知△ABC的内角A，B，C的对边分别是a，b，c，若 $A + C = 2 B$ ， $\sqrt{3} a^{2} + \sqrt{3} c^{2} - 2 a c s i n B = 9 \sqrt{3}$ ，则 $b =$ （）

A、 $3 \sqrt{3}$ B、3 C、6 D、 $\sqrt{3}$

查看试题解析
8. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E，F，Q，H分别为所在棱的中点，则直线HC与平面EFQ所成角的正弦值为（）

A、 $\frac{\sqrt{2}}{3}$ B、 $\frac{\sqrt{2}}{6}$ C、 $\frac{1}{6}$ D、 $\frac{\sqrt{2}}{12}$

查看试题解析

二、多选题

9. 如图，在直三棱妵 $A B C - A_{1} B_{1} C_{1}$ 中，D，G，E分别为所在棱的中点， $\vec{A B} = 4 \vec{A F}$ ，三棱柱 $A B C - A_{1} B_{1} C_{1}$ 挖去两个三棱锥 $A - E F G$ ， $B_{1} - B C_{1} D$ 后所得的几何体记为 $Ω$ ，则（）

A、 $Ω$ 有7个面 B、 $Ω$ 有13条棱 C、 $Ω$ 有7个顶点 D、平面 $B C_{1} D ∩$ 平面 $A B B_{1} A_{1} = B D$

查看试题解析
10. 已知复数 $z = \frac{2 + 11 i}{2 + i}$ ，则（）

A、 $| z | = 5$ B、 $\bar{z} = 3 - 4 i$ C、z在复平面内对应的点在第二象限 D、 $z - 4 i \in R$

查看试题解析
11. 已知△ABC的内角A，B，C的对边分别是a，b，c，若 $A = \frac{π}{6}$ ， $a = 1$ ， $b = \sqrt{3}$ ，则C可能为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{2}$ D、 $\frac{2 π}{3}$

查看试题解析
12. 如图，一个正八面体的八个面分别标有数字1，2，3，…，8，任意抛掷一次该正八面体，观察它与地面接触的面上的数字，得到样本空间 $Ω = {1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7 ， 8}$ ，若事件 $A = {2 ， 4 ， 6 ， 8}$ ，事件 $B = {1 ， 3 ， 5 ， 8}$ ，事件 $C = {1 ， 6 ， 7 ， 8}$ ，则（）

A、事件A，B相互独立 B、事件A，C相互独立 C、事件B，C相互独立 D、 $P (A B C) = P (A) P (B) P (C)$

查看试题解析

三、填空题

13. 已知一组数据为2，6，5，4，7，9，8，10，则该组数据的 $80 %$ 分位数为.

查看试题解析
14. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = \sqrt{6}$ ， $| \vec{b} | = \sqrt{2}$ ，且 $| \vec{a} + \vec{b} | = 2 \sqrt{3}$ ，则 $\vec{a} \cdot \vec{b} =$ ；向量 $\vec{a}$ 与 $\vec{b}$ 的夹角的余弦值为

查看试题解析
15. 已知一个圆锥的轴截面是一个边长为6的正三角形，则该圆锥的外接球的表面积为.

查看试题解析
16. 咸阳市的标志性建筑清渭楼，古朴典雅，蔚为壮观．为了测量清渭楼最高点M与其附近一观测点N之间的距离，取水平方向距离1200米的P，Q两点，测得 $∠ Q P M = \frac{π}{3}$ ， $∠ Q P N = \frac{π}{4}$ ， $∠ P Q M = \frac{π}{6}$ ， $∠ P Q N = \frac{5 π}{12}$ ，其中点M，N，P，Q在同一铅垂面内，则M，N两点之间的距离为米．

查看试题解析

四、解答题

17. 已知向量 $\vec{a} = (- 2 ， 5)$ ， $\vec{b} = (1 ， - 1)$ ， $\vec{c} = (6 ， λ)$ ．

(1)、若 $(2 \vec{a} + \vec{b}) ∥ \vec{c}$ ，求 $λ$ 的值；

(2)、若 $(\vec{a} - 3 \vec{b}) ⊥ \vec{c}$ ，求 $λ$ 的值．

查看试题解析
18. 已知 $△ A B C$ 的内角A，B，C的对边分别是a，b，c， $△ A B C$ 的面积为S，且 $2 S - \sqrt{3} b c c o s A = 0$ ．

(1)、求角A的大小；

(2)、若 $a = 7$ ， $b c = 40$ ，求 $△ A B C$ 的周长．

查看试题解析
19. 某果园大约还有5万个蜜桔等待出售，原销售方案是所有蜜桔都以25元/千克的价格进行销售，为了更好地促进销售，需对蜜桔质量进行质量分析，以便做出合理的促销方案．现从果园内随机采摘200个蜜桔进行测重，其质量分别在 $[25 ， 35)$ ， $[35 ， 45)$ ， $[45 ， 55)$ ， $[55 ， 65)$ ， $[65 ， 75)$ ， $[75 ， 85]$ （单位：克）中，其频率分布直方图如图所示．

(1)、求m的值；

(2)、估计该果园这200个蜜桔的平均质量为多少克/个；（同一组的数据以该组区间的中点值为代表）

(3)、以样本估计总体，若低于55克的蜜桔以140元/百个进行销售，不低于55克的蜜桔以160元/百个进行销售，试问该果园的收益是否会更高？

查看试题解析
20. 如图，某铁质零件由一个正三棱台和一个正三棱柱组成，已知正三棱柱的底面边长与高均为1cm，正三棱台的下底面边长为2cm，且正三棱台的高为1cm，现有一盒这种零件共重 $650 \sqrt{3} g$ （不包含盒子的质量），取铁的密度为 $7.8 g / c m^{3}$ ．

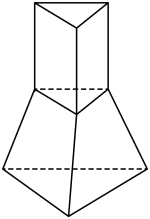(1)、试问该盒中有多少个这样的零件？

(2)、如果要给这盒零件的每个零件表面涂上一种特殊的材料，试问共需涂多少 $c m^{2}$ 的材料？

查看试题解析
21. 某学校派甲、乙两人组成“少年队”参加射击比赛，每轮比赛由甲、乙各射击一次，已知甲每轮射中的概率为 $\frac{1}{2}$ ，乙每轮射中的概率为 $\frac{2}{3}$ ．在每轮比赛中，甲和乙射中与否互不影响，各轮比赛结果也互不影响．

(1)、求“少年队”在一轮比赛中恰好射中1次的概率；

(2)、求“少年队”在三轮比赛中恰好射中3次的概率．

查看试题解析
22. 如图，在四棱锥 $M - A B C D$ 中， $A D ∥ B C$ ， $A C ⊥ C D$ ， $B C = 2 A D$ ， △MAD为等边三角形，平面 $M A D ⊥$ 平面ABCD，点N在棱MD上，直线 $M B / /$ 平面ACN．

(1)、证明： $M N = 2 N D$ ．

(2)、设二面角 $M - A C - D$ 的平面角为 $α$ ，直线CN与平面ABCD所成的角为 $θ$ ，若 $t a n α$ 的取值范围是 $[3 ， 3 \sqrt{3}]$ ，求 $t a n θ$ 的取值范围．

查看试题解析