云南省保山市文山州2022-2023学年高二下学期期末考试数学试题
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 在复平面内,复数对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知 , 则( )A、 B、 C、3 D、4. 蜜蜂的巢房是令人惊叹的神奇天然建筑物.巢房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱形的底,由三个相同的菱形组成.巢中被封盖的是自然成熟的蜂蜜.如图是一个蜂巢的正六边形开口 , 下列说法正确的是( )
 A、 B、 C、 D、5. 已知首项为1的等比数列满足成等差数列,则公比( )A、 B、 C、2 D、6. 在疫情防控期间,某社区开展了“疫情要防住,文明在行动”核酸检测志愿服务活动.活动期间,要安排5名志愿者完成 , , 三项工作.已知每项工作至少有一人参加,每人只能参加一项工作,则不同的安排方式共有( )A、150种 B、120种 C、90种 D、60种7. 已知双曲线的右焦点为 , 以为圆心,为半径的圆与双曲线的一条渐近线的两个交点为 . 若 , 则该双曲线的离心率为( )A、 B、 C、 D、8. 已知函数是定义在上的奇函数,且当时不等式成立,若 , , , 则 , , 的大小关系是( )A、 B、 C、 D、
A、 B、 C、 D、5. 已知首项为1的等比数列满足成等差数列,则公比( )A、 B、 C、2 D、6. 在疫情防控期间,某社区开展了“疫情要防住,文明在行动”核酸检测志愿服务活动.活动期间,要安排5名志愿者完成 , , 三项工作.已知每项工作至少有一人参加,每人只能参加一项工作,则不同的安排方式共有( )A、150种 B、120种 C、90种 D、60种7. 已知双曲线的右焦点为 , 以为圆心,为半径的圆与双曲线的一条渐近线的两个交点为 . 若 , 则该双曲线的离心率为( )A、 B、 C、 D、8. 已知函数是定义在上的奇函数,且当时不等式成立,若 , , , 则 , , 的大小关系是( )A、 B、 C、 D、二、多选题
-
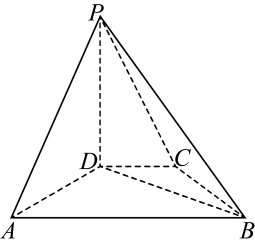
9. 下列结论错误的是( )A、若 , 则 B、若 , 则 C、若 , , 则 D、若 , 的最小值为10. 已知函数 , 则( )A、的最小正周期为 B、的图象关于点对称 C、的最小值为0 D、的图象关于直线对称11. 为随机事件,已知 , , 下列结论中正确的是( )A、若为互斥事件,则 B、若为互斥事件,则 C、若相互独立,则 D、若 , 则相互独立12. 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;阳马指底面为矩形,一侧棱垂直于底面的四棱锥;鳖臑指四个面均为直角三角形的四面体.如图,在堑堵中, , , 则下列说法正确的是( )
 A、四棱锥为阳马 B、三棱锥为鳖臑 C、当三棱锥的体积最大时,二面角的余弦值为 D、记四棱锥的体积为 , 三棱锥的体积为 , 则
A、四棱锥为阳马 B、三棱锥为鳖臑 C、当三棱锥的体积最大时,二面角的余弦值为 D、记四棱锥的体积为 , 三棱锥的体积为 , 则三、填空题
-
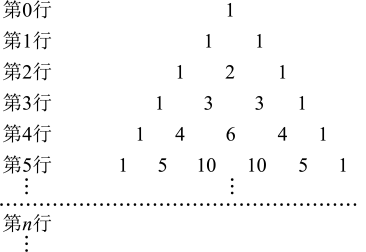
13. 设函数 , 则曲线在点处的切线方程是.14. 过点 , 且焦点在轴上的抛物线的标准方程是.15. 已知三棱锥中,平面 , , , 则三棱锥的外接球的表面积为.16. “杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.如图所示,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数之和,例如第4行的第3个数6为第3行中两个3的和.记“杨辉三角”第行的第个数为 , 请用组合数第行写出 , 则.
四、解答题
-
17. 已知数列的前项和为 , , .(1)、求的通项公式;(2)、设数列满足: , 记的前项和为 , 求.18. 记的内角 , , 的对边分别为 , , , 已知 , .(1)、求的大小;(2)、为上一点,从下列条件①、条件②中任选一个作为已知,求线段的最大值.
条件①:为的角平分线;条件②:为边上的中线.
19. 民族要复兴,乡村要振兴,合作社助力乡村产业振兴,农民专业合作社已成为新型农业经营主体和现代农业建设的中坚力量,为实施乡村振兴战略作出了巨大的贡献.已知某主要从事手工编织品的农民专业合作社共有100名编织工人,该农民专业合作社为了鼓励工人,决定对“编织巧手”进行奖励,为研究“编织巧手”是否与年龄有关,现从所有编织工人中抽取40周岁以上(含40周岁)的工人24名,40周岁以下的工人16名,得到的数据如表所示.“编织巧手”
非“编织巧手”
总计
年龄40岁
19
年龄<40岁
10
总计
40
参考公式: , 其中 .
参考数据:
0.100
0.050
0.010
0.005
2.706
3.841
6.635
7.879
(1)、请完成答题卡上的列联表,并根据小概率值的独立性检验,分析“编织巧手”与“年龄”是否有关;(2)、为进一步提高编织效率,培养更多的“编织巧手”,该农民专业合作社决定从上表中的非“编织巧手”的工人中采用分层抽样的方法抽取6人参加技能培训,再从这6人中随机抽取2人分享心得,求这2人中恰有1人的年龄在40周岁以下的概率.