广东省江门市鹤山市2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 下列各数中,没有平方根的是( )A、65 B、 C、 D、2. 计算的结果是( )A、6 B、 C、2 D、3. 下列说法中,正确的有( )
①正比例函数一定是一次函数;
②一次函数一定是正比例函数;
③速度一定,路程s是时间t的一次函数;
④圆的面积是圆的半径r的正比例函数.
A、1个 B、2个 C、3个 D、4个4. 下列各统计量中,表示一组数据波动程度的量是( )A、平均数 B、众数 C、方差 D、频率5. 如图,在平行四边形ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则平行四边形ABCD的周长为( )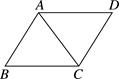 A、26 cm B、24 cm C、20 cm D、18 cm6. 一支蜡烛长20cm,若点燃后每小时燃烧5cm,则燃烧剩余的长度y(cm)与燃烧时间x(时)之间的函数关系的图象大致为(如图)( )A、
A、26 cm B、24 cm C、20 cm D、18 cm6. 一支蜡烛长20cm,若点燃后每小时燃烧5cm,则燃烧剩余的长度y(cm)与燃烧时间x(时)之间的函数关系的图象大致为(如图)( )A、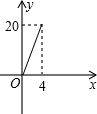 B、
B、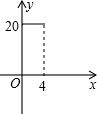 C、
C、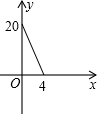 D、
D、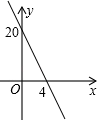 7. 如图,在等腰梯形中, , 、相交于点O , 则图中全等三角形共( )
7. 如图,在等腰梯形中, , 、相交于点O , 则图中全等三角形共( ) A、1对 B、2对 C、3对 D、4对8. 若以A(-0.5,0)、B(2,0)、C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,点A的坐标为 , 点B在直线上运动,当线段AB最短时,点B的坐标为( )
A、1对 B、2对 C、3对 D、4对8. 若以A(-0.5,0)、B(2,0)、C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,点A的坐标为 , 点B在直线上运动,当线段AB最短时,点B的坐标为( ) A、 B、 C、 D、10. 如图是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形面积是13,小正方形面积是1,直角三角形两条直角边长分别为a、b , 则的值是( )
A、 B、 C、 D、10. 如图是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形面积是13,小正方形面积是1,直角三角形两条直角边长分别为a、b , 则的值是( ) A、4 B、5 C、12 D、1
A、4 B、5 C、12 D、1二、填空题
-
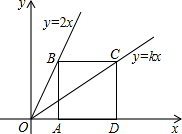
11. 平行四边形中, , 则°.12. 成立的条件是.13. 已知一次函数图象过(1,2)且y随x的增大则减小,请写出一个符合条件的函数解析式.14. 已知样本中各数据、…与样本平均数的差的平方和是: , 则样本方差 .15. 如图,点B、C分别在两条直线和上,点A、D是轴上两点,已知四边形ABCD是正方形,则k值为.
三、解答题
-
16. 当自变量x取何值时,函数y= x+1与y=5x+17的值相等?这个函数值是多少?17. 某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数
6
7
8
9
人数
1
5
2
(1)、填空:10名学生的射击成绩的众数是 , 中位数是.(2)、这10名学生的平均成绩为.(3)、若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有是优秀射手.18. 如图,从正方形中载去两个面积分别为和的正方形和 , 求留下部分的总面积. 19. 如图,是等腰三角形, .
19. 如图,是等腰三角形, . (1)、利用直尺和圆规作边上的中线(不写做法,保留作图痕迹);(2)、延长到D , 使 , 连接 , .
(1)、利用直尺和圆规作边上的中线(不写做法,保留作图痕迹);(2)、延长到D , 使 , 连接 , .求证:四边形是菱形.
20. 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点. (1)、以格点为顶点画 , 使三边长为:3, , ;(2)、求的面积.21. 我国古代数学著作《九章算术》中有一个问题,原文是:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何.(丈、尺是长度单位,1丈=10尺).意思是有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少?
(1)、以格点为顶点画 , 使三边长为:3, , ;(2)、求的面积.21. 我国古代数学著作《九章算术》中有一个问题,原文是:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何.(丈、尺是长度单位,1丈=10尺).意思是有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少? 22. 如图,在平行四边形中,过点A作变边于点E , 点F在边上,且 .
22. 如图,在平行四边形中,过点A作变边于点E , 点F在边上,且 . (1)、求证:四边形是矩形;(2)、若平分 , 且 , 求线段的长.
(1)、求证:四边形是矩形;(2)、若平分 , 且 , 求线段的长.

