广东省云浮市2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 下列二次根式,是最简二次根式的是( )A、 B、 C、 D、2. 以下列各组数为边长,能构成直角三角形的是( )A、1,2,2 B、1,2,3 C、1,1, D、4,5,63. 如图,要测定被池塘隔开的A , B两点的距离,可以在池塘外选一点C , 连接、 , 并分别找出它们的中点、 , 连接 . 现测得 , 则等于( )
 A、42m B、52m C、56m D、64m4. 下列式子化简正确的是( )A、 B、 C、 D、5. 甲、乙两个样本,计算得平均数均为10,方差 , , 则样本的数据波动大的是( )A、甲 B、乙 C、甲乙都一样 D、无法判断6. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、
A、42m B、52m C、56m D、64m4. 下列式子化简正确的是( )A、 B、 C、 D、5. 甲、乙两个样本,计算得平均数均为10,方差 , , 则样本的数据波动大的是( )A、甲 B、乙 C、甲乙都一样 D、无法判断6. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、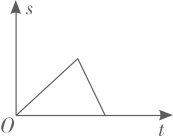 B、
B、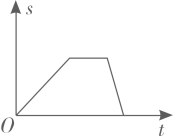 C、
C、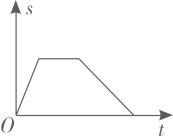 D、
D、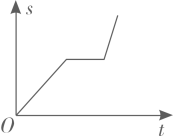 7. 正方形的一条对角线长为2,则这个正方形的边长为( )A、1 B、 C、 D、8. 如图,的对角线 , 相交于点 , 添加下列条件仍不能判断四边形是菱形的是( )
7. 正方形的一条对角线长为2,则这个正方形的边长为( )A、1 B、 C、 D、8. 如图,的对角线 , 相交于点 , 添加下列条件仍不能判断四边形是菱形的是( ) A、 B、 C、 D、9. 一次函数的图象过点 , . 下列结论不正确的是( )A、随的增大而减小 B、函数图象经过第一、二、四象限 C、是方程的解 D、函数图象与轴交于点10. 如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )
A、 B、 C、 D、9. 一次函数的图象过点 , . 下列结论不正确的是( )A、随的增大而减小 B、函数图象经过第一、二、四象限 C、是方程的解 D、函数图象与轴交于点10. 如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )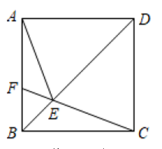 A、35° B、40° C、45° D、50°
A、35° B、40° C、45° D、50°二、填空题
-
11. 若二次根式在实数范围内有意义,则x的取值范围是 .12. 正比例函数的图象如图所示,则 .
 13. 计算的结果是 .14. 甲参加某商场员工招聘,通过计算机、语言表达和商品知识三项测试,成绩分别为:85、90、92,若相应分别按的比例计算成绩,则甲的综合得分为分.15. 如图,已知在矩形中, , , 则 .
13. 计算的结果是 .14. 甲参加某商场员工招聘,通过计算机、语言表达和商品知识三项测试,成绩分别为:85、90、92,若相应分别按的比例计算成绩,则甲的综合得分为分.15. 如图,已知在矩形中, , , 则 . 16. 把函数的图象向上平移3个单位长度后,得到的新图象对应的函数解析式为 , 这两图象的位置关系是 .17. 如图,在中,对角线 , 相交于点 , 过点作交于 , 若 , , , 则的长为 .
16. 把函数的图象向上平移3个单位长度后,得到的新图象对应的函数解析式为 , 这两图象的位置关系是 .17. 如图,在中,对角线 , 相交于点 , 过点作交于 , 若 , , , 则的长为 .
三、解答题
-
18. 计算:19. 如图,在平行四边形中,对角线、交于点 , , , 垂足分别为、 . 求证: .
 20. 如图,在平面直角坐标系中,直线分别与轴、轴交于点、 , 且与直线交于点 .
20. 如图,在平面直角坐标系中,直线分别与轴、轴交于点、 , 且与直线交于点 . (1)、求出、、的坐标;(2)、直接写出关于的不等式的解集;21. 如图,在中, , , , 点D是外一点,连接 , , 且 , .
(1)、求出、、的坐标;(2)、直接写出关于的不等式的解集;21. 如图,在中, , , , 点D是外一点,连接 , , 且 , . (1)、求的长(2)、求四边形的面积22. 某校八年级举办中华优秀传统文化知识竞赛,用简单随机抽样的方法,从该年级全体1600名学生中抽取若干名,其竞赛成绩如图.
(1)、求的长(2)、求四边形的面积22. 某校八年级举办中华优秀传统文化知识竞赛,用简单随机抽样的方法,从该年级全体1600名学生中抽取若干名,其竞赛成绩如图. (1)、此抽样调查的样本容量为;(2)、被抽取学生成绩的众数为 , 中位数为;(3)、若规定成绩大于或等于90分为优秀等级,试估计该年级获优秀等级的学生人数.23. 游泳已纲入中考选考科目,某游泳馆针对学生游泳训练需求,推出以下两种收费方式.
(1)、此抽样调查的样本容量为;(2)、被抽取学生成绩的众数为 , 中位数为;(3)、若规定成绩大于或等于90分为优秀等级,试估计该年级获优秀等级的学生人数.23. 游泳已纲入中考选考科目,某游泳馆针对学生游泳训练需求,推出以下两种收费方式.方式一:不购买年卡,每次游泳付费元.
方式二:先购买年卡,每张年卡元,仅限本人一年内使用,凭卡游泳,每次游泳再付费元.设你在一年内来此游泳馆游泳的次数为次,选择方式一的总费用为元,选择方式二的总费用为元.
(1)、请分别写出 , 与之间的函数表达式;(2)、如果你在一年内来此游泳馆游泳的次数超过次,选择哪种方式更划算?


