广东省湛江市经济开发区2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 化简二次根式 $\sqrt{3^{2}} =$ （）

A、9 B、3 C、 $\pm 9$ D、 $\pm 3$

查看试题解析
2. 若 $\sqrt{x + 2}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x > 2$ B、 $x > - 2$ C、 $x \geq - 2$ D、 $x \geq 2$

查看试题解析
3. 下列各组数中，不能构成直角三角形的是（）

A、3，4，5 B、5，12，13 C、6，8，10 D、7，14，15

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} - \sqrt{2} = 1$ C、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ D、 $\sqrt{3} \div \sqrt{2} = \frac{3}{2}$

查看试题解析
5. 菱形具有而平行四边形不一定具有的性质是（）

A、对边相等 B、对角线相等 C、对角线互相平分 D、对角线互相垂直

查看试题解析
6. 若数据甲1，2，3，4，5的方差为 ${S_{甲}}^{2}$ ，数据2，3，3，3，4的方差为 ${S_{乙}}^{2}$ ，则（）

A、 ${S_{甲}}^{2} > {S_{乙}}^{2}$ B、 ${S_{甲}}^{2} = {S_{乙}}^{2}$ C、 ${S_{甲}}^{2} < {S_{乙}}^{2}$ D、无法确定

查看试题解析
7. 在同一平面直角坐标系中，若一次函数 $y = x - 1$ 与 $y = - x + 3$ 图象交于点M ，则点M的坐标为（）

A、 $(2 ， 1)$ B、 $(1 ， 0)$ C、 $(0 ， - 1)$ D、 $(3 ， 0)$

查看试题解析
8. 如图，直线 $y = k x + b$ 经过 $A (2 ， 1)$ ， $B (- 1 ， - 2)$ 两点，则不等式 $k x + b > - 2$ 的解集为（）

A、 $x > - 2$ B、 $x > - 1$ C、 $x > 1$ D、 $x > 2$

查看试题解析
9.
如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD的面积比是（）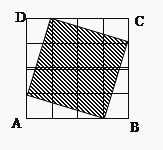

A、3 ：4 B、5 ：8 C、9 ：16 D、1 ：2

查看试题解析
10. 如图1所示，四边形 $A B C D$ 为正方形，对角线 $A C$ ， $B D$ 相交于点 $O$ ，动点 $P$ 在正方形的边和对角线上匀速运动．如果点 $P$ 运动的时间为 $x$ ，点 $P$ 与点 $A$ 的距离为 $y$ ，且表示 $y$ 与 $x$ 的函数关系的图象大致如图2所示，那么点 $P$ 的运动路线可能为（）

A、 $A \to B \to C \to D$ B、 $A \to B \to C \to A$ C、 $A \to C \to B \to D$ D、 $A \to B \to D \to A$

查看试题解析

二、填空题

11. 化简： $\sqrt{4 a^{3}}$ =.

查看试题解析
12. 已知矩形ABCD中，若AC=8，则BD＝．

查看试题解析
13. 将一次函数 $y = - 2 x - 3$ 的图象沿y轴向上平移5个单位后，得到的图象对应的函数关系式为．

查看试题解析
14. 请写出一个一次函数的解析式，使它的图象经过点 $A (2 ， - 4)$ ：．

查看试题解析
15. 如图，在矩形ABCD中无重叠放入面积分别为acm²和bcm²（a＞b）的两张正方形纸片，则图中空白部分的面积为cm² ．

查看试题解析

三、解答题

16. 计算： $\sqrt{8} - \sqrt{18} + \sqrt{32}$ ．

查看试题解析
17. 计算： ${(\sqrt{2} - 1)}^{2} - (3 + 2 \sqrt{2}) (3 - 2 \sqrt{2})$ ．

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 30 °$ ， $B C = 2$ ，求 $A C$ 的长．

查看试题解析
19. 在 $▱$ ABCD中，DE⊥AB ， BF⊥CD ，垂足分别是E、F ．求证：AE=CF.

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $A B = 24$ ， $A D = 7$ ， $A C = 25$ ．求 $▱ A B C D$ 的面积．

查看试题解析
21. 某市为了节约生活用水，计划制定每位居民统一的月用水量标准，然后根据标准，实行分段收费.为此，对居民上年度的月均用水量进行了抽样调查，并根据调查结果绘制了上年度月均用水量的频数分布直方图（图中分组含最低值，不含最高值），请根据图中信息解答下列问题：

(1)、本次调查的居民人数为人；

(2)、本次调查的居民月均用水量的中位数落在频数分布直方图中的第小组内（从左至右数）；

(3)、当地政府希望让85%左右居民的月均用水量低于制定的月用水量标准，根据上述调查结果，你认为月用水量标准（取整数）定为多少吨时较为合适？

查看试题解析
22. 下图是某汽车行驶的路程S（千米）与时间t（分钟）的函数关系图，观察图中所提供的信息，解答下列问题：

(1)、汽车在前16分钟内的平均速度是千米/分钟；

(2)、汽车在中途停留的时间为分钟；

(3)、直接写出S与t的函数关系式．

查看试题解析
23. 如图，在平面直角坐标系中，直线 $y = - \frac{3}{4} x + b$ 分别与x轴，y轴交于点A ， B ，且点A的坐标为 $(4 ， 0)$ ，四边形 $A B C D$ 是正方形．

(1)、填空： $b =$ ；

(2)、求点D的坐标；

(3)、若点P是线段 $A B$ 上的一个动点（点A ， B除外），试探究：在x上方是否存在另一个点Q ，使得以O ， B ， P ， Q为顶点的四边形是菱形？若存在，请求出点Q的坐标；若不存在，请说明理由．

查看试题解析