广东省肇庆市高要区2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 在函数 $y = \sqrt{x - 2}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x \geq 2$ C、 $x > 2$ D、 $x \leq - 2$

查看试题解析
2. 一次函数y=2x+1的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$ D、 $\frac{\sqrt{4}}{2} = \sqrt{2}$

查看试题解析
4. 平行四边形 $A B C D$ 中，已知 $∠ A = 50 °$ ，则其邻角 $∠ B$ 的度数为（）

A、 $40 °$ B、 $130 °$ C、 $100 °$ D、 $50 °$

查看试题解析
5. 计算 $\sqrt{(\sqrt{3} - 2)^{2}}$ 的值为（）

A、 $\sqrt{3} - 2$ B、 $\sqrt{3} + 2$ C、 $2 - \sqrt{3}$ D、 $- \sqrt{3} - 2$

查看试题解析
6. 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）

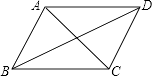A、当AB=BC时，四边形ABCD是菱形 B、当AC⊥BD时，四边形ABCD是菱形 C、当∠ABC=90°时，四边形ABCD是矩形 D、当AC=BD时，四边形ABCD是正方形

查看试题解析
7. 在学校的卫生检查中，规定各班的教室卫生成绩占30%，环境卫生成绩占40%，个人卫生成绩占30%．八年级一班这三项成绩分别为85分，90分和95分，则该班卫生检查的总成绩是（）

A、88分 B、89分 C、90分 D、91分

查看试题解析
8. 已知 $A (2 ， 0)$ ， $B (0 ， 2)$ ，下列四个点中与A、B在同一条直线上的是（）

A、 $(1 ， 2)$ B、 $(- 1 ， 3)$ C、 $(- 2 ， - 3)$ D、 $(3 ， - 2)$

查看试题解析
9. 一组数据：5、5、6、4，若添加一个数据5，则发生变化的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
10. 已知函数 $y = k x + b$ 的图象如图所示，则关于 $x$ 的不等式 $k (x + 3) + b < 0$ 的解集是（）

A、 $x > - 1$ B、 $x < - 1$ C、 $x < 2$ D、 $x > 2$

查看试题解析

二、填空题

11. 比较大小： $2 \sqrt{5}$ $3 \sqrt{3}$ （在横线上填上<、>或=）．

查看试题解析
12. 在平面直角坐标系中，点M（5，－12）到原点的距离是.

查看试题解析
13. 已知正比例函数 $y = k x$ （k是常数， $k \neq 0$ ），y的值随着x的值的增大而增大，请写出一个满足条件的正比例函数的解析式： $y =$

查看试题解析
14. 甲、乙、丙、丁四名学生最近 $4$ 次数学考试平均分都是 $112$ 分，方差 $S_{甲}^{2} = 2.2$ ， $S_{乙}^{2} = 6.6$ ， $S_{丙}^{2} = 7.4$ ， $S_{丁}^{2} = 10.8$ ，则这四名学生的数学成绩最稳定的是．

查看试题解析
15. 已知平行四边形 $A B C D$ 面积为16， $A C$ 、 $B D$ 相交于点O，则 $△ C O D$ 的面积为．

查看试题解析

三、解答题

16. 计算： $\sqrt{27} \times \sqrt{50} \div \sqrt{6}$ ．

查看试题解析
17. 如下图，在 $Δ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ 于点 $D$ ， $B C = 3 c m ， A B = 5 c m$ ．

(1)、求 $Δ A B C$ 的面积；

(2)、求线段 $C D$ 的长．

查看试题解析
18. 如图，直线 $l_{1} ： y = x - 1$ 与直线 $l_{2} ： y = - \frac{1}{2} x + 2$ 在同一直角坐标中交于点 $A (2 ， 1)$ .

(1)、直接写出方程组 ${\begin{array}{l} x - y = 1 \\ x + 2 y = 4 \end{array}$ 的解是.

(2)、请判断三条直线 $y = x - 1 ， y = - \frac{1}{2} x + 2 ， y = \frac{1}{4} x + \frac{1}{2}$ ，是否经过同一个点，请说明理由.

查看试题解析
19. 如图，菱形ABCD的对角线相交于点O，∠BAD＝60°，菱形ABCD的周长为24．

(1)、求对角线BD的长；

(2)、求菱形ABCD的面积．

查看试题解析
20. 小红打算买一束百合和康乃馨组合的鲜花，在“母亲节”送给妈妈．已知买2支康乃馨和3支百合共需花费28元，买3支康乃馨和2支百合共需花费27元．

(1)、求买一支康乃馨和一支百合各需多少元？

(2)、小红准备买康乃馨和百合共9支，且百合花支数不少于康乃馨支数．设买这束鲜花所需费用为w元，康乃馨有x支，求w与x之间的函数关系式，并直接写出满足上述条件且费用最少的买花方案．

查看试题解析
21. 某螺母加工厂为了解工人的日均生产能力，随机调查了一部分工人日均加工螺母的数量、根据调查结果，绘制出如下统计图①和图②．

请根据相关信息，解答下列问题：

(1)、本次接受调查的工人人数为；图①中m的值为；

(2)、求所抽取工人日均加工螺母个数数据的平均数、众数和中位数；

(3)、若该工厂共有加工螺母的工人84人，则日均加工螺母数为16个的约有多少人？

查看试题解析
22. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = - \frac{1}{2} x + 5$ 的图象 $l_{1}$ 分别与x ， y轴交于A ， B两点，正比例函数的图象 $l_{2}$ 与 $l_{1}$ 交于点 $C (m ， 4)$ ．

(1)、求m的值及 $l_{2}$ 的解析式；

(2)、求 $S_{△ A O C} ： S_{△ B O C}$ 的值；

(3)、一次函数 $y = k x + 1$ 的图象为 $l_{3}$ ，且 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 不能围成三角形，直接写出k的值．

查看试题解析
23. 如图，在平面直角坐标系中， $O$ 为坐标原点，矩形 $O A B C$ 的顶点 $A (16 ， 0) 、 C (0 ， 12)$ ，将矩形 $O A B C$ 的一个角沿直线 $B D$ 折叠，使得点 $A$ 落在对角线 $O B$ 上的点 $E$ 处，折痕与 $x$ 轴交于点 $D$ ．

(1)、线段 $O B$ 的长度为；

(2)、在 $Δ O E D$ 中， $O D^{2}$ ▲ $O E^{2} + D E^{2}$ （在横线上填上<、>或=），并分别求出 $Δ O E D$ 的三条边长；

(3)、求点 $E$ 的坐标．

查看试题解析