广东省珠海市香洲区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 下列各组数是三角形的三边长,其中不能构成直角三角形的是( )A、3,4,5 B、4,5,6 C、6,8,10 D、5,12,133. 下列4个点中,在一次函数的图象上的点是( )A、 B、 C、 D、4. 甲、乙、丙三个旅行团的游客人数相等,且平均年龄都是32岁,游客年龄的方差分别是 , , , 导游小王最喜欢带游客年龄相近的团,则他应选( )A、甲团 B、乙团 C、丙团 D、无法确定5. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )
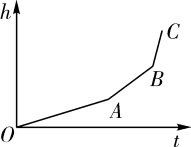 A、
A、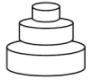 B、
B、 C、
C、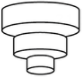 D、
D、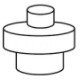 6. 如图,在中,是斜边上的中线,若 , 则的度数为( )
6. 如图,在中,是斜边上的中线,若 , 则的度数为( ) A、 B、 C、 D、7. 已知一次函数的图象如图所示,则k,b的取值范围是( )
A、 B、 C、 D、7. 已知一次函数的图象如图所示,则k,b的取值范围是( ) A、 , B、 , C、 , D、 ,8. 如图,矩形的对角线与相交于点O , , P , Q分别为 , 的中点,则的长度为( )
A、 , B、 , C、 , D、 ,8. 如图,矩形的对角线与相交于点O , , P , Q分别为 , 的中点,则的长度为( ) A、 B、2 C、3 D、49. 某招聘考试规定按笔试成绩占 , 面试成绩占计算最终得分,小李笔试90分、面试80分;小吴笔试80分、面试90分;小叶笔试60分、面试70分,则最终得分最高的是( )A、小李 B、小吴 C、小叶 D、小李和小吴一样最高10. 关于的一次函数(k为常数且),①当时,此函数为正比例函数;②无论取何值,此函数图象必经过;③若函数图象同时经过点和点( , 为常数),则;④无论取何值,此函数图象都不可能同时经过第二、三、四象限,上述结论中正确的序号有( )A、①② B、②③ C、②④ D、③④
A、 B、2 C、3 D、49. 某招聘考试规定按笔试成绩占 , 面试成绩占计算最终得分,小李笔试90分、面试80分;小吴笔试80分、面试90分;小叶笔试60分、面试70分,则最终得分最高的是( )A、小李 B、小吴 C、小叶 D、小李和小吴一样最高10. 关于的一次函数(k为常数且),①当时,此函数为正比例函数;②无论取何值,此函数图象必经过;③若函数图象同时经过点和点( , 为常数),则;④无论取何值,此函数图象都不可能同时经过第二、三、四象限,上述结论中正确的序号有( )A、①② B、②③ C、②④ D、③④二、填空题
-
11. 若式子有意义,则x的取值范围为 .12. 平行四边形中, , 则的度数为度.13. 如图,一次函数的图象与x轴交于点 , 则关于x的不等式的解集为 .
 14. 小李将能够活动的菱形学具拉伸成为图1所示形状,并测得时 , 接着,她又将这个学具拉伸成为图2所示的正方形,则此时的长度为 .
14. 小李将能够活动的菱形学具拉伸成为图1所示形状,并测得时 , 接着,她又将这个学具拉伸成为图2所示的正方形,则此时的长度为 . 15. 如图,在中, , 点、分别为、边的三等分点(靠近点),已知 , , 则斜边的长为 .
15. 如图,在中, , 点、分别为、边的三等分点(靠近点),已知 , , 则斜边的长为 .
三、解答题
-
16. 计算: .17. 如图,在 ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
 18. 请解决我国古代数学著作《九章算术》中的一个问题:一根竹子原来高10尺,从A处折断,折断后竹子顶端B点落在离竹子底端O点3尺处,求折断处离地面(即)的高度是多少尺?
18. 请解决我国古代数学著作《九章算术》中的一个问题:一根竹子原来高10尺,从A处折断,折断后竹子顶端B点落在离竹子底端O点3尺处,求折断处离地面(即)的高度是多少尺? 19. 已知 , 求下列各式的值;(1)、;(2)、 .20. 为普及“垃圾分类”知识,某校组织全校学生参加了垃圾分类主题知识竞赛,为了解竞赛成绩,随机抽样调查了七、八年级各10名学生的成绩x(单位:分),分数如下:
19. 已知 , 求下列各式的值;(1)、;(2)、 .20. 为普及“垃圾分类”知识,某校组织全校学生参加了垃圾分类主题知识竞赛,为了解竞赛成绩,随机抽样调查了七、八年级各10名学生的成绩x(单位:分),分数如下:七年级10名学生竞赛成绩:92,83,99,89,99,86,100,81,92,99;
八年级10名学生竞赛成绩中分布在的成绩如下:93,94,95.
【整理数据】:
年级
七年级
2
m
2
4
八年级
1
2
3
4
【分析数据】:
年级
平均数
众数
中位数
方差
七年级
92
a
b
45.8
八年级
94
100
c
38.2
根据以上提供的信息,回答下列问题:
(1)、填空: , , , ;(2)、该校七年级学生有300人,全部参加竞赛,请估计七年级成绩高于90分的人数;(3)、请你根据以上信息,推断哪个年级的成绩更好,并说明理由.(写出一条理由即可)21. 如图,在Rt△CDG中,∠CGD=90°,分别以△CDG的两边为边向外作正方形ABCD和正方形CEFG,连接DE、GB,过点G作AB的垂线GM,垂足为M,交DC于点K. (1)、猜想与的数量关系,并证明你的结论;(2)、比较矩形与正方形的面积大小关系,并说明理由.22. 图中折线表示一骑车人小明离学校的距离与离开学校时间的关系.小明匀速骑行到达图书馆,在图书馆阅读一段时间,然后返回学校;回学校途中,匀速骑行后减速,继续匀速骑行回到学校.请你根据相关信息,解答下列问题:
(1)、猜想与的数量关系,并证明你的结论;(2)、比较矩形与正方形的面积大小关系,并说明理由.22. 图中折线表示一骑车人小明离学校的距离与离开学校时间的关系.小明匀速骑行到达图书馆,在图书馆阅读一段时间,然后返回学校;回学校途中,匀速骑行后减速,继续匀速骑行回到学校.请你根据相关信息,解答下列问题: (1)、图书馆与学校距离是 , 小明在图书馆阅读时长为h,小明前往图书馆的平均速度是 , 当时,y关于x的解析式为;(2)、小明刚开始离开学校的时候,另一骑车人小华同时出发,从图书馆沿着相同路线以速度匀速前往学校,到达学校后马上骑车以速度匀速前往图书馆.
(1)、图书馆与学校距离是 , 小明在图书馆阅读时长为h,小明前往图书馆的平均速度是 , 当时,y关于x的解析式为;(2)、小明刚开始离开学校的时候,另一骑车人小华同时出发,从图书馆沿着相同路线以速度匀速前往学校,到达学校后马上骑车以速度匀速前往图书馆.①请问小华速度为何范围时,小华与小明可以在时相遇;
②当时,请求出x为何值时小华与小明相距 .
23. 如图,在平面直角坐标系中,矩形的顶点A在x轴正半轴,点D在矩形的边上,与相交于点G , , 对角线解析式为: . (1)、求D点坐标和k的值;(2)、平行于x轴的直线m , 从原点O出发,以每秒1个单位长度的速度沿方向移动,到达点C时停止,运动时间为t秒,平移过程中,直线m与线段、分别交于点E、F .
(1)、求D点坐标和k的值;(2)、平行于x轴的直线m , 从原点O出发,以每秒1个单位长度的速度沿方向移动,到达点C时停止,运动时间为t秒,平移过程中,直线m与线段、分别交于点E、F .①记线段的长度为L , 当点F在点E右边时,求L与t的函数关系式;
②当四边形为平行四边形时,求t的值,并说明此时的平行四边形是否为菱形;
(3)、在(2)的情况下,以为边向下作等边(点P在线段下方),与重叠部分的面积记为S . 填空:当秒时,S的值;当E点落在中点时,S的值 .