广东省韶关市翁源县2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、3.14159265 B、 C、 D、2. 在平面直角坐标系中,所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图, , , 则( )
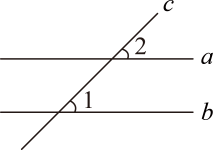 A、 B、 C、 D、4. 若a>b , 则下列结论不一定成立的是( )A、a>-b B、a+1>b+1 C、 D、-a<-b5. 如图,在数轴上表示关于x的不等式组的解集是( )
A、 B、 C、 D、4. 若a>b , 则下列结论不一定成立的是( )A、a>-b B、a+1>b+1 C、 D、-a<-b5. 如图,在数轴上表示关于x的不等式组的解集是( ) A、 B、 C、 D、6. 下列各命题是假命题的是( )A、两直线平行,同旁内角互补 B、若两个数 , 则这两个数为相反数 C、对顶角相等 D、如果 , 那么7. 每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础,为了解某校七年级600名学生的睡眠时间,从12个班级中随机抽取50名学生进行调查,下列说法不正确的是( )A、该校七年级600名学生的睡眠时间是总体 B、样本容量是50 C、12个班级是抽取的一个样本 D、每名七年级学生的睡眠时间是个体8. 若 =0,则a+b的值为( )A、﹣2 B、﹣1 C、0 D、29. 点到y轴的距离等于( )A、 B、3 C、2 D、110. 用加减消元法解方程组其解题步骤如下:(1) , 得 , 解得;(2) , 得 , 解得;所以原方程组的解为
A、 B、 C、 D、6. 下列各命题是假命题的是( )A、两直线平行,同旁内角互补 B、若两个数 , 则这两个数为相反数 C、对顶角相等 D、如果 , 那么7. 每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础,为了解某校七年级600名学生的睡眠时间,从12个班级中随机抽取50名学生进行调查,下列说法不正确的是( )A、该校七年级600名学生的睡眠时间是总体 B、样本容量是50 C、12个班级是抽取的一个样本 D、每名七年级学生的睡眠时间是个体8. 若 =0,则a+b的值为( )A、﹣2 B、﹣1 C、0 D、29. 点到y轴的距离等于( )A、 B、3 C、2 D、110. 用加减消元法解方程组其解题步骤如下:(1) , 得 , 解得;(2) , 得 , 解得;所以原方程组的解为则下列说法正确的是( )
A、步骤(1)(2)都不对 B、步骤(1)(2)都对 C、本题不适宜用加减消元法解 D、加减消元法不能用两次二、填空题
-
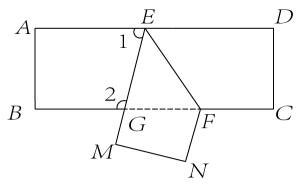
11. 4的平方根是12. 已知方程 , 用含x的式子表示y , 则 .13. 不等式2x﹣6>0的解集是 .14. 已知方程组 , 则= .15. 如图,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G , 点D , C分别折叠到点M , N的位置上,若 , 则 .
三、解答题
-
16. 解方程组:17. 解不等式组: ,请结合题意填空,完成本题的解答:(1)、解不等式①,得:;(2)、解不等式②,得:;(3)、把不等式①和②的解集在数轴上表示出来:
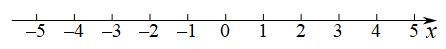 (4)、原不等式组的解集为: .18. 在等式中,当时, , 当时, .(1)、求k , b的值;(2)、求当时,y的值.19. 如图,在直角坐标系中,各点的坐标分别为 , , ;
(4)、原不等式组的解集为: .18. 在等式中,当时, , 当时, .(1)、求k , b的值;(2)、求当时,y的值.19. 如图,在直角坐标系中,各点的坐标分别为 , , ; (1)、若把向上平移2个单位,再向左平移1个单位得到 , 写出的坐标,并在图中画出平移后图形.(2)、求出三角形的面积.20. 网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
(1)、若把向上平移2个单位,再向左平移1个单位得到 , 写出的坐标,并在图中画出平移后图形.(2)、求出三角形的面积.20. 网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.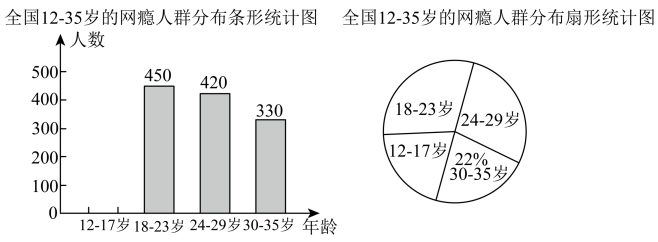
请根据图中的信息,回答下列问题:
(1)、这次抽样调查中共调查了 ▲ 人,并请补全条形统计图;(2)、扇形统计图中岁部分的圆心角的度数是;(3)、据报道,目前我国岁网瘾人数约为2000万,请估计其中岁的人数.21. 如图,已知 , 试说明 . 下面是部分推导过程.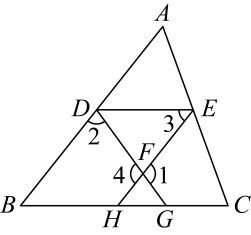
请你在括号内填上推导依据或内容:
证明:(已知),( ),
▲ ▲ (等量代换),
( ),
▲ ( ),
(已知),
▲ ( ),
( ).
22. 为加强中小学生安全教育,某校组织了“防溺水、交通安全”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格也相同),购买2个足球和3个篮球共需374元;足球单价是篮球单价的2倍少9元.(1)、请用方程组求足球和篮球的单价各是多少元?(2)、根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,则学校最多可以购买多少个足球?23. 将一副三角板中的两个直角顶点叠放在一起(如图①),其中 , , , , 设 .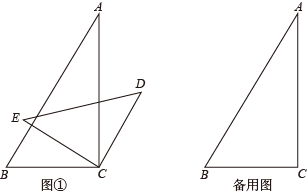 (1)、填空: , ;(用含的代数式表示)(2)、若 , 求的度数;(3)、若三角板不动,三角板绕顶点转动一周,当等于多少度时?
(1)、填空: , ;(用含的代数式表示)(2)、若 , 求的度数;(3)、若三角板不动,三角板绕顶点转动一周,当等于多少度时?