广东省汕头市澄海区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-10 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点B(2,-3)到x轴的距离为( )A、-2 B、2 C、-3 D、32. 为了解某校2400名学生的视力情况,从中抽查了200名学生的视力进行统计分析,下列四个判断正确的是( )A、2400名学生是总体 B、样本容量是200名学生 C、200名学生的视力是总体的一个样本 D、200名学生是总体的一个样本3. 下列等式一定成立的是( )A、 B、 C、 D、4. 若一个正数a的平方根是与 , 则a的值是( )A、5 B、3 C、 D、95. 若点P( , )在第二象限,则的取值范围是( )A、 B、 C、 D、或6. 把一副三角板按如图所示平放在桌面上,点恰好落在的延长线上, , 则的大小为( )
 A、 B、 C、 D、7. 若关于、的方程组的解为 , 则( )A、 , B、 , C、 , D、 ,8. 若是二元一次方程的一个解,则( )A、3 B、-3 C、0 D、99. 下列不等式的变形正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 如图,已知直线 , , , 则等于( )
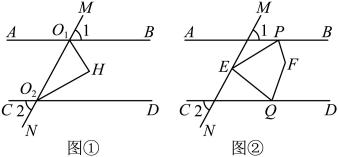
A、 B、 C、 D、7. 若关于、的方程组的解为 , 则( )A、 , B、 , C、 , D、 ,8. 若是二元一次方程的一个解,则( )A、3 B、-3 C、0 D、99. 下列不等式的变形正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 如图,已知直线 , , , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 121的平方根是 .12. 将点先向右平移5个单位,再向下平移4个单位得到点 , 则点的坐标为 .13. 不等式组的整数解有个.
三、解答题
-
14. 如图,直线、相交于点O , , 垂足为O , 且 , 求的度数.

四、填空题
-
15. 在平面直角坐标系中,对于平面内任意一点 , 规定以下两种变化:
① , ② . 按照该规定:
计算: , .
五、解答题
-
16. 计算: .17. 解不等式: .18. 已知与互为相反数.(1)、求的平方根;(2)、解关于x的方程 .19. 为贯彻落实市教育局“课后服务”的文件精神,某校积极开展学生课后服务活动.为更好了解学生对课后服务活动的需求,学校随机抽取了部分学生,进行“我最喜欢的课后服务活动”的调查(每位学生只能选其中一种活动),并将调查结果整理后,形成如下两个不完整的统计图:请根据所给信息解答以下问题:
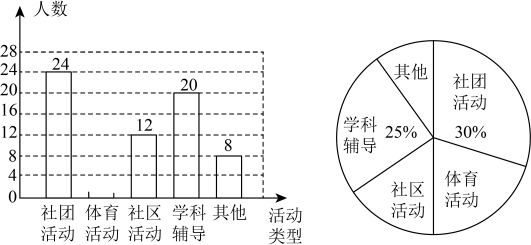 (1)、这次参与调查的学生人数为 ▲ 人,请将条形统计图补充完整;(2)、扇形统计图中“社团活动”所在扇形的圆心角度数为;(3)、若该校共有学生1800人,请估计最喜欢的课后服务活动是“社团活动”的人数约为多少人?20. 如图,已知 , 与互余, , 垂足为G , 求证: .
(1)、这次参与调查的学生人数为 ▲ 人,请将条形统计图补充完整;(2)、扇形统计图中“社团活动”所在扇形的圆心角度数为;(3)、若该校共有学生1800人,请估计最喜欢的课后服务活动是“社团活动”的人数约为多少人?20. 如图,已知 , 与互余, , 垂足为G , 求证: . 21. 现有甲乙两个工程队参加一条道路的改造施工,受条件限制,每天只能由一个工程队施工.若甲工程队先单独施工3天,再由乙工程队单独施工5天,则可以完成380米施工任务;若甲工程队先单独施工2天,再由乙工程队单独施工4天,则可以完成280米的施工任务.(1)、求甲、乙两个工程队平均每天分别能完成多少米施工任务?(2)、要改造的道路全长1800米,先由甲工程队先单独施工若干天,再由乙工程队单独完成剩下的施工任务,若工期不能超过40天,那么甲工程队至少要施工多少天?
21. 现有甲乙两个工程队参加一条道路的改造施工,受条件限制,每天只能由一个工程队施工.若甲工程队先单独施工3天,再由乙工程队单独施工5天,则可以完成380米施工任务;若甲工程队先单独施工2天,再由乙工程队单独施工4天,则可以完成280米的施工任务.(1)、求甲、乙两个工程队平均每天分别能完成多少米施工任务?(2)、要改造的道路全长1800米,先由甲工程队先单独施工若干天,再由乙工程队单独完成剩下的施工任务,若工期不能超过40天,那么甲工程队至少要施工多少天?
-
-