广东省湛江市徐闻县2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示的车标，可以看作由平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各数：3.1415926， $\frac{π}{2}$ ， $- \sqrt{4}$ ， $\frac{1}{7}$ ，其中是无理数的是（）

A、3.1415926 B、 $\frac{π}{2}$ C、 $\frac{1}{7}$ D、- $\sqrt{4}$

查看试题解析
3. 点 $P (0 ， - 6)$ （）

A、在x轴上 B、在y轴上 C、在第二象限 D、在第四象限

查看试题解析
4. 下列事件中适合采用抽样调查的是（）

A、对乘坐飞机的乘客进行安检 B、学校招聘教师，对应聘人员进行面试 C、对“天宫2号”零部件的检查 D、对端午节期间市面上粽子质量情况的调查

查看试题解析
5. 估计 $\sqrt{13}$ 的值在（）

A、1和2之间 B、2和3之间 C、3和4之间 D、5和6之间

查看试题解析
6. 在下列命题中，假命题是（）

A、如果两个角是互为邻补角，那么这两个角互补 B、如果两条直线被第三条直线所截，那么同位角相等 C、在同一平面内，过一点有且只有一条直线与已知直线垂直 D、如果两条直线都与第三条直线平行，那么这两条直线也互相平行

查看试题解析
7. 如图是一轰炸机群的飞行队形示意图，若在图上建立平面直角坐标，使最后两架轰炸机分别位于点 $M (- 1 ， 1)$ 和点 $N (- 1 ， - 3)$ ，则第一架轰炸机位于的点P的坐标是（）

A、 $(3 ， - 1)$ B、 $(- 1 ， 3)$ C、 $(- 3 ， - 1)$ D、 $(3 ， 0)$

查看试题解析
8. 若m＜n，则下列各式一定正确的是（）

A、 $- 2 m < - 2 n$ B、 $\frac{m}{3} > \frac{n}{3}$ C、 $1 - m > 1 - n$ D、 $m + 1 > n + 1$

查看试题解析
9. 某校举行篮球赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得 1分．七年级一班在16场比赛中得26分．设该班胜x场，负y场，则根据题意，下列方程组中正确的是（）

A、 ${\begin{matrix} y = - x + 2 \\ y = x - 1 \end{matrix}$ B、 ${\begin{matrix} y = - x + 2 \\ y = x - 1 \end{matrix}$ C、 ${\begin{matrix} x + y = 16 \\ x + 2 y = 26 \end{matrix}$ D、 ${\begin{matrix} x + y = 16 \\ 2 x + y = 26 \end{matrix}$

查看试题解析
10. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点 $(1 ， 1)$ ，第2次接着运动到点 $(2 ， 0)$ ，第3次接着运动到点 $(3 ， 2)$ ， …按这样的运动规律，经过第2023次运动后，动点P的坐标是（）

A、 $(2022 ， 1)$ B、 $(2023 ， 0)$ C、 $(2023 ， 1)$ D、 $(2023 ， 2)$

查看试题解析

二、填空题

11. 已知方程 $2 x^{2 n - 1} - 7 y = 10$ 是关于x、y的二元一次方程，则n= ．

查看试题解析
12. 如图，计划把河中的水引到水池M中，可以先过M点作MC⊥AB，垂足为C，然后沿MC开渠，则能使所开的渠最短，这种设计方案的根据是.

查看试题解析
13. $\sqrt[3]{8} + \sqrt{{(- 3)}^{2}} =$ ．

查看试题解析
14. 在平面直角坐标系xOy中，点M的坐标是（1，2）， $M N ∥ x$ 轴， $M N = 3$ ，则点N的坐标是．

查看试题解析
15. 若关于x的不等式组 ${\begin{array}{l} 3 x - 2 \geq 1 \\ 2 x - a \leq 5 \end{array}$ ，有且只有3个整数解，则a的取值范围是．

查看试题解析

三、解答题

16. 解方程组： ${\begin{array}{l} 3 x + 4 y = 9 \\ x + y = 1 \end{array}$ ．

查看试题解析
17. 解下列不等式组，并把解集在数轴上表示出来：
${\begin{array}{l} 5 x - 2 > 4 x - 1 \\ \frac{1}{2} x + 1 \geq - 2 + \frac{3}{2} x \end{array}$

查看试题解析
18. 如图：已知 $A B ∥ C D$ ， $∠ 1 = ∠ 2$ ， $∠ D F E = 100 °$ ．求 $∠ D B C$ 的度数．

查看试题解析
19. 羊城书香浓郁，某校为进一步提升学生阅读水平，组织学生参加阅读大赛．从中抽取部分学生阅读大赛的成绩（得分取正整数，满分为100分）进行统计分析，请根据下列尚未完成的统计图表，解答问题．
组别
分数段
频数
百分比
一
50.5~60.5
16
8%
二
60.5~70.5
30
15%
三
70.5~80.5
50
25%
四
80.5~90.5
a
40%
五
90.5~100.5
24
12%

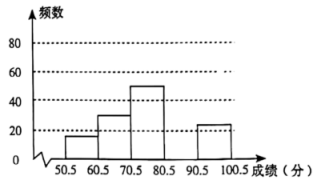(1)、本次抽样调查的样本容量为 ▲ ，表中 $a =$ ▲ ，并补全频数分布直方图；

(2)、若把各组的分数段所占的百分比绘制成扇形统计图，则第三组对应的扇形圆心角的度数是；

(3)、该校一共组织2000名学生参加阅读大赛，若抽取的样本具有较好的代表性，且成绩超过80分为优秀，请估计该校学生中阅读能力优秀的约有多少人？

查看试题解析
20. 已知2a+1的平方根是±3，3a+2b+4的立方根是-2，求4a-5b+5的算术平方根．

查看试题解析
21. 如图，△ABC的顶点A（-1，4），B（-4，-1），C（1，1）.若△ABC向右平移4个单位长度，再向下平移3个单位长度得到△A'B'C'，且点C的对应点坐标是C'.

(1)、画出△A'B'C'，并直接写出点C'的坐标；

(2)、若△ABC内有一点P（a，b）经过以上平移后的对应点为P'，直接写出点P'的坐标；

(3)、求△ABC的面积.

查看试题解析
22. 2022年北京冬奥会、冬残奥会的纪念品得到广大民众的喜爱，某校想要购买A型、B型两种纪念品．已知购买2件A型纪念品和1件B型纪念品共需150元；购买3件A型纪念品和2件B型纪念品共需245元．

(1)、求A型纪念品和B型纪念品的单价；

(2)、学校现需一次性购买A型纪念品和B型纪念品共100个，要求购买的总费用不超过5000元，则最多可以购买多少个A型纪念品？

查看试题解析
23. 如图，已知 $∠ M A B = 56 °$ ，点B（与点A不重合）是 $A B$ 边上一点，作 $B N ∥ A M$ ，点P是射线 $A M$ 上一动点（与点A不重合）， $B C$ 、 $B D$ 分别平分 $∠ A B P$ 和 $∠ P B N$ ，分别交射线 $A M$ 于点C ， D ．

(1)、求 $∠ A B N$ ， $∠ C B D$ 的度数；

(2)、探究：当点P运动时， $∠ A P B$ 与 $∠ A D B$ 之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律；

(3)、当点P运动到使 $∠ A C B = ∠ A B D$ 时，求出 $∠ A B C$ 的度数．

查看试题解析

组别	分数段	频数	百分比
一	50.5~60.5	16	8%
二	60.5~70.5	30	15%
三	70.5~80.5	50	25%
四	80.5~90.5	a	40%
五	90.5~100.5	24	12%