2023年浙教版数学八年级上册1.1 认识三角形 同步测试（提高版）

试卷更新日期：2023-08-10 类型：同步测试

进入 出卷网 下载

一、选择题（每题3分，共30分）

  • 1. 如图中三角形的个数是（　　）

    A、1 B、2 C、3 D、4

    查看试题解析

  • 2. 下列说法：①等边三角形是等腰三角形；②等腰三角形也可能是直角三角形；③三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形；④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.其中正确的有(　　)
    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 3. 若长度为x，2，3的三条线段能组成一个三角形，则x的值可能为（　　）
    A、6 B、5 C、1 D、3

    查看试题解析

  • 4. 嘉兴某校项目化学习小组研究“三角形周长”的课题，将3根木棒首尾相连围成一个三角形，其中两根木棒的长分别为3cm、10cm，则该三角形的周长可能是（    ）
    A、18cm B、19cm C、20cm D、21cm

    查看试题解析

  • 5. 如图，AE是△ABC的中线，点D是BE上一点，若BD=5 ， CD=9 ， 则CE的长为（ ）

    A、5 B、6 C、7 D、8

    查看试题解析

  • 6. 如图所示，∠1=∠2，∠3=∠4，则下列结论正确的有（　　）

    ①AD平分∠BAF；②AF平分∠BAC；③AE平分∠DAF；④AF平分∠DAC；⑤AE平分∠BAC．

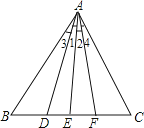    A、4个 B、3个 C、2个 D、1个

    查看试题解析

  • 7. 适合下列条件的△ABC中，直角三角形的个数为（    ）

    ①∠A：∠B：∠C＝1：2：3；②∠A+∠B＝∠C；③∠A＝90°-∠B；④∠A＝∠B＝2∠C.

    A、1 B、2 C、3 D、4

    查看试题解析

  • 8. 如图，在△ABC中，AD是角平分线，AE是高，已知∠B=50°，∠C=60°，那么∠EAD的度数为（     ）

    A、5° B、15° C、25° D、35° 

    查看试题解析

  • 9. 如图，AB//DC ， 以点A为圆心，小于AC的长为半径作圆弧，分别交AB ， AC于E ， F两点，再分别以E ， F为圆心，以大于12EF长为半径作圆弧两条弧交于点G ， 作射线AG交CD于点H ， 若∠C=120° ， 则∠AHD=（ ）

    A、120° B、30° C、150° D、60°

    查看试题解析

  • 10. 如图，从△ABC各顶点作平行线AD∥EB∥FC ， 各与其对边或其延长线相交于点D，E，F.若△ABE的面积为S1 ， △AFC的面积为S2 ， △EDC的面积为S3 ， 只要知道下列哪个值就可以求出△DEF的面积（    ）

    A、S1+S2 B、S1+S2+S3 C、S3 D、S1+S2+2S3

    查看试题解析

二、填空题（每空4分，共24分）

  • 11. 图中以AB为边的三角形共有个．

    查看试题解析

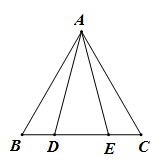  • 12. 一个三角形的两边长分别是3和7，则它的第三边的长为x，则x的范围为 ．

    查看试题解析

  • 13. 已知BD、CE是△ABC的高，直线BD、CE相交所成的锐角为40°，则∠A的度数是 .

    查看试题解析

  • 14. 如图，在ΔABC中，∠B=30° ， ∠C=70° ， AE ， AD分别是ΔABC的角平分线和高线，则∠DAE的度数是 ．

    查看试题解析

  • 15. 如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是8cm2 ， 则阴影部分△BEF面积等于cm2 ．

    查看试题解析

  • 16. 如图，△ABC中，点D在线段BC边上，且不与端点重合，点E，F是线段AD的三等分点，记△BDF的面积为S1 ， △ACE的面积为S2 ， 若S1＋S2＝3，则△ABC的面积为 ．

    查看试题解析

三、解答题（共9题，共66分）

  • 17. 在△ABC中，∠A=∠B=12∠C ，
    (1)、求∠A、∠B、∠C的度数；
    (2)、△ABC按边分类，属于什么三角形？△ABC按角分类，属于什么三角形？

    查看试题解析

  • 18. 在△ABC中，BC＝8，AB＝1；
    (1)、若AC是整数，求AC的长；
    (2)、已知BD是△ABC的中线，若△ABD的周长为10，求△BCD的周长．

    查看试题解析

  • 19. 小王准备用一段长30m的篱笆围成一个三角形形状的场地，用于饲养家兔，已知第一条边长为am，由于受地势限制，第二条边长只能是第一条边长的2倍多2m.
    (1)、请用a表示第三条边长.
    (2)、问第一条边长可以为7m吗？请说明理由.

    查看试题解析

  • 20. 已知三角形ABC的三边为a ， b ， c；
    (1)、若a＝2，b＝7，c为最长边且为整数，求三角形ABC的周长；
    (2)、化简：|a+b﹣c|﹣|b﹣a﹣c|+|a+b+c|．

    查看试题解析

  • 21. 如图，已知△ABC.

    (1)、若AB=3，AC=4，求BC的取值范围；
    (2)、点D为BC延长线上一点，过点D作DE∥AC，交BA的延长线于点E，若∠E=60°，∠ACD=125°，求∠B的度数.

    查看试题解析

  • 22. 如图，在△ABC中，∠B＝30°，∠C＝65°，AE⊥BC于E，AD平分∠BAC，

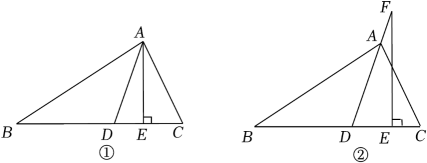    (1)、求∠DAE的度数；
    (2)、如图②，若把“AE⊥BC”变成“点F在DA的延长线上，FE⊥BC”，其它条件不变，求∠DFE的度数.

    查看试题解析

  • 23. 如图，在△ABC中，∠B=40°，∠C=110°.

    (1)、画出下列图形：

    ①BC边上的高AD；②∠A的角平分线AE.

    (2)、试求∠DAE的度数.

    查看试题解析

  • 24. 如图，在△ABC中，AE是边BC上的高.

    (1)、若AD是BC边上的中线，AE=3cm ， S△ABC=12cm2 ， 求DC的长；
    (2)、若AD是∠BAC的平分线，∠B=40° ， ∠C=50° ， 求∠DAE的大小.

    查看试题解析

  • 25. 如图①，△ABC的角平分线BD、CE相交于点P．

    (1)、如果∠A＝80°，求∠BPC的度数；
    (2)、如图②，过P点作直线MN，分别交AB和AC于点M和N，且MN平行于BC，则有∠MPB+∠NPC＝90°−12∠A．若将直线MN绕点P旋转，

    （ⅰ）如图③，试探索∠MPB、∠NPC、∠A三者之间的数量关系是否依然成立，并说明理由；

    （ⅱ）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的延长线上时，如图④，试问（ⅰ）中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立？若不成立，请给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由．

    查看试题解析