2023年浙教版数学八年级上册1.1 认识三角形同步测试（培优版）

试卷更新日期：2023-08-10 类型：同步测试

进入出卷网下载

一、选择题（每题2分，共20分）

1. 根据下列条件，能确定三角形形状的是（    ）
⑴最小内角是20°；    ⑵最大内角是100°；

⑶最大内角是89°；    ⑷三个内角都是60°；

⑸有两个内角都是80°．

A、（1）、（2）、（3）、（4） B、（1）、（3）、（4）、（5） C、（2）、（3）、（4）、（5） D、（1）、（2）、（4）、（5）

查看试题解析
2. 给出下列命题：
①三条线段组成的图形叫三角形；②三角形相邻两边组成的角叫三角形的内角；

③三角形的角平分线是射线；

④三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外；

⑤任何一个三角形都有三条高、三条中线、三条角平分线；

⑥三角形的三条角平分线交于一点，且这点在三角形内.

正确的命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 用12根等长的火柴棒拼成一个三角形，火柴棒不允许剩余，重叠和折断，则能摆出不同的三角形的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 平面内，将长分别为1，5，1，1，d的线段，顺次首尾相接组成凸五边形（如图），则d可能是（）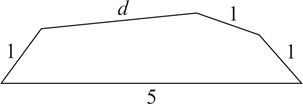

A、1 B、2 C、7 D、8

查看试题解析
5. 五条长度均为整数厘米的线段：a₁ ， a₂ ， a₃ ， a₄ ， a₅ ，满足a₁＜a₂＜a₃＜a₄＜a₅ ，其中a₁＝1厘米，a₅＝9厘米，且这五条线段中的任意三条都不能构成三角形，则a₃＝（）

A、3厘米 B、4厘米 C、3或4厘米 D、不能确定

查看试题解析
6. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE中点，且△ABC的面积等于4cm² ，则阴影部分图形面积等于（）.

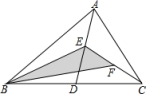A、1cm² B、2cm² C、0.5cm² D、1.5cm²

查看试题解析
7. 已知△ABC的两条中线的长分别为5、10，若第三条中线的长也是整数，则第三条中线长的最大值（）

A、7 B、8 C、14 D、15

查看试题解析
8. 如图△ABC中，∠A=96°，延长BC到D，∠ABC与∠ACD的平分线相交于点A₁∠A₁BC与∠A₁CD的平分线相交于点A₂ ，依此类推，∠A₄BC与∠A₄CD的平分线相交于点A₅ ，则∠A₅的度数为（）

A、19.2° B、8° C、6° D、3°

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B$ 的度数为α．点P在边 $B C$ 上（点P不与点B，点C重合），作 $P D ⊥ A B$ 于点D，连接 $P A$ ，取 $P A$ 上一点E，使得 $E C = E P$ ，连接 $E D$ ， $C E$ 并延长 $C E$ 交 $A B$ 于点F之后，有 $E C = E D = E A = E P$ ．若记 $∠ A P C$ 的度数为x，则下列关于 $∠ D E F$ 的表达式正确的是（）

A、 $∠ D E F = 2 x - 3 α$ B、 $∠ D E F = 2 α$ C、 $∠ D E F = 2 α - x$ D、 $∠ D E F = 180 - 3 α$

查看试题解析
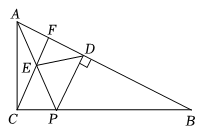10. 如图，A，B，C分别是线段A₁B，B₁C，C₁A的中点，若△ABC的面积是1，那么△A₁B_lC₁的面积是（）

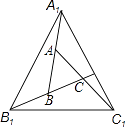A、4 B、5 C、6 D、7

查看试题解析

二、填空题（每空3分，共18分）

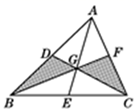
11. 已知在△ABC中，∠A＋∠B＜∠C，则△ABC是三角形．（填“直角”、“锐角”或“钝角”）

查看试题解析
12. 若三角形的周长为13，且三边均为整数，则满足条件的三角形有种．

查看试题解析
13. 如图， $D ， E ， F$ 分别是 $Δ A B C$ 的边 $A B ， B C ， A C$ 上的中点，连接 $A E ， B F ， C D$ 交于点G， $A G ： G E = 2 ： 1$ ， $Δ A B C$ 的面积为6，设 $Δ B D G$ 的面积为 $S_{1}$ ， $Δ C G F$ 的面积为 $S_{2}$ ，则 $S_{1} + S_{2} =$ ．

查看试题解析
14. 将两张三角形纸片如图摆放，量得∠1+∠2+∠3+∠4=220°，则∠5的度数为.

查看试题解析
15. 如图，在△ABC中，已知点D、E、F分别为BC、AD、CE的中点，且 $S_{Δ A B C}$ =4cm² ，则 $s_{阴影}$ = ．

查看试题解析
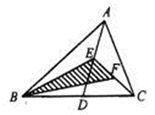16. 等腰三角形一腰上的高线与另一腰夹角为40°，则该三角形的顶角为。

查看试题解析

三、解答题（共11题，共82分）

17. 已知a，b，c是△ABC的三边长。

(1)、若a，b，c满足|a-b|+|b-c|=0，试判断△ABC的形状。

(2)、若a，b，c满足(a-b)(b-c)=0，试判断△ABC的形状。

查看试题解析
18. 过A、B、C、D、E五个点中任意三点画三角形；

(1)、其中以AB为一边可以画出个三角形；

(2)、其中以C为顶点可以画出个三角形．

查看试题解析
19. 在 $△ A B C$ 中， $A B = 8$ ， $A C = 1$ ．

(1)、若 $B C$ 是整数，求 $B C$ 的长．

(2)、已知 $A D$ 是 $△ A B C$ 的中线，若 $△ A C D$ 的周长为10，求三角形 $A B D$ 的周长．

查看试题解析
20. 已知△ABC的周长为33cm，AD是BC边上的中线， $A B = \frac{3}{2} A C$ ．

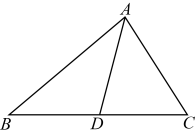(1)、如图，当AC＝10cm时，求BD的长．

(2)、若AC＝12cm，能否求出DC的长？为什么？

查看试题解析
21. 已知在 $△ A B C$ 中， $∠ A 、 ∠ B 、 ∠ C$ 的对边分别为 $a 、 b 、 c$ .

(1)、化简代数式 $| a + b - c | + | b - a - c | =$ .

(2)、若 $∠ B = ∠ A + 18 °$ ， $∠ C = ∠ B + 18 °$ ，求 $△ A B C$ 的各内角度数；

查看试题解析
22. 如图1，AB与CD相交于点O，若∠D=38°，∠B=28°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试求：

(1)、∠P的度数；

(2)、设∠D=α，∠B=β，∠DAP= $\frac{1}{3}$ ∠DAB，∠DCP= $\frac{1}{3}$ ∠DCB，其他条件不变，如图2，试问∠P与∠D、∠B之间存在着怎样的数量关系（用α、β表示∠P），直接写出结论．

查看试题解析
23. 如图，在△ABC中，AE，CD分别是∠BAC， ∠ACB的平分线，且AE，CD相交于点F.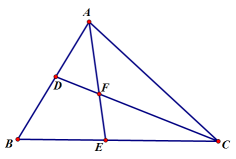

(1)、若∠BAC=80°，∠ACB=40°，求∠AFC的度数；

(2)、若∠B=80°，求∠AFC的度数；

(3)、若∠B=x°，用含x的代数式表示∠AFC的度数.

查看试题解析
24. 如图，直线l∥线段BC，点A是直线l上一动点.在△ABC中，AD是△ABC的高线，AE是∠BAC的角平分线.

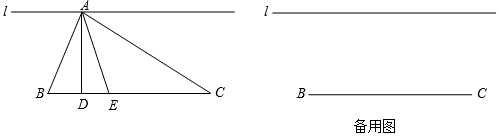(1)、如图，若∠ABC＝65°，∠BAC＝80°，求∠DAE的度数；

(2)、当点A在直线l上运动时，探究∠BAD，∠DAE，∠BAE之间的数量关系，并画出对应图形进行说明.

查看试题解析
25. △ABC中，AD是∠BAC的角平分线，AE是△ABC的高．

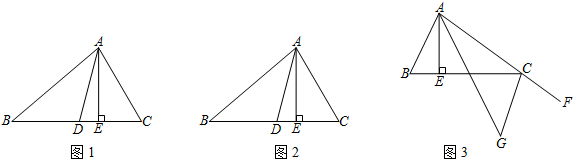(1)、如图1，若∠B＝40°，∠C＝60°，请说明∠DAE的度数；

(2)、如图2（∠B＜∠C），试说明∠DAE、∠B、∠C的数量关系；

(3)、如图3，延长AC到点F，∠CAE和∠BCF的角平分线交于点G，请直接写出∠G的度数．

查看试题解析
26. 有三个面积都等于1的三角形，它们的底及对应的高分别记为： $a_{1}$ ， $a_{2}$ ， $a_{3}$ 及 $h_{1}$ ， $h_{2}$ ， $h_{3}$ ．

(1)、 $a_{1} h_{1} =$ ， $a_{2} h_{2} =$ ， $a_{3} h_{3} =$ ．
如果 $a_{1} < a_{2} < a_{3}$ ，则用 $h_{1}$ ， $h_{2}$ ， $h_{3}$ 填空：＜＜；

(2)、如果 $a_{1} = m$ ， $a_{2} = m + 1$ ， $a_{3} = m + 2$ （ $m > 0$ ），试比较 $h_{1} - h_{2}$ ， $h_{2} - h_{3}$ 的大小；

(3)、如果 $a_{1} = n (n + 1)$ ， $a_{2} = (n + 1) (n + 2)$ ， $a_{3} = (n + 2) (n + 3)$ （ $n > 0$ ）．求 $h_{1} + h_{2} + h_{3}$ 的值（用含n的代数式表示）．

查看试题解析
27. 已知 $Δ A B C$ 的面积是 $120$ ，请完成下列问题：

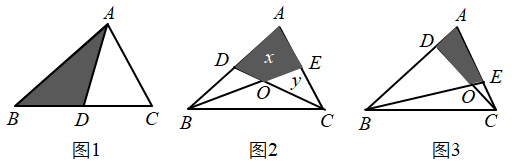(1)、如图1所示，若 $A D$ 是 $Δ A B C$ 的 $B C$ 边上的中线，则 $Δ A B D$ 的面积 $Δ A C D$ 的面积．（填“ $>$ ”“ $<$ ”或“ $=$ ”）

(2)、如图2所示，若 $C D$ ， $B E$ 分别是 $Δ A B C$ 的 $A B$ ， $A C$ 边上的中线，求四边形 $A D O E$ 的面积可以用如下方法：连接 $A O$ ，由 $A D = D B$ 得： $S_{Δ A D O} = S_{Δ B D O}$ ，同理： $S_{Δ C E O} = S_{Δ A E O}$ ，设 $S_{Δ A D O} = x$ ， $S_{Δ C E O} = y$ 则 $S_{Δ B D O} = x$ ， $S_{Δ A E O} = y$ ．由题意得： $S_{Δ A B E} = \frac{1}{2} S_{Δ A B C} = 60$ ， $S_{Δ A D C} = \frac{1}{2} S_{Δ A B C} = 60$ ，可列方程组为 ${\begin{array}{l} 2 x + y = 60 \\ x + 2 y = 60 \end{array}$ ，解得，通过解这个方程组可得四边形 $A D O E$ 的面积为．

(3)、如图3所示， $A D ： D B = 1 ： 3$ ， $C E ： A E = 1 ： 2$ ，请你计算四边形 $A D O E$ 的面积，并说明理由．

查看试题解析

2023年浙教版数学八年级上册1.1 认识三角形 同步测试（培优版）

一、选择题（每题2分，共20分）

二、填空题（每空3分，共18分）

三、解答题（共11题，共82分）

2023年浙教版数学八年级上册1.1 认识三角形同步测试（培优版）