2023-2024学年北师大版数学八年级上册1.2一定是直角三角形吗 同步练习(培优卷)
试卷更新日期:2023-08-09 类型:同步测试
一、选择题
-
1. 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )A、b2-c2=a2 B、a:b:c=3:4:5 C、∠A:∠B:∠C=9:12:15 D、∠C=∠A-∠B2. 下列条件中,不能判断是直角三角形的是( )A、三角形三条边的比为 B、三角形三条边满足关系式 C、三角形三条边的比为 D、三角形三个内角满足关系式3. △ABC的三个内角分别为∠A,∠B,∠C,三条边分别为a,b,c.下列条件,能判断△ABC是直角三角形的是( )A、 B、 C、 D、4. 由线段a,b,c组成的三角形中,是直角三角形的是( ).A、a=1,b=2,c=3 B、a=1,b= , c= C、a=2,b=3,c=5 D、a=3,b=4,c=55. 下列长度的四组线段中,可以构成直角三角形的是( )A、1,2,3 B、 , 2, C、4,5,6 D、8,15,196. 满足下列条件的 , 其中不是直角三角形的是( )A、 B、 C、 D、7. 老师布置了任务:过直线上一点C作的垂线.在没有直角尺的情况下,嘉嘉和淇淇利用手头的学习工具给出了如图所示的两种方案,下列判断正确的是( )
方案Ⅰ:
①利用一把有刻度的直尺在上量出 . ②分别以D,C为圆心,以和为半径画圆弧,两弧相交于点E.③作直线 , 即为所求的垂线.
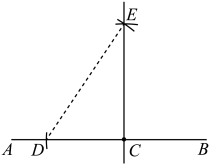
方案Ⅱ:
取一根笔直的木棒,在木棒上标出M,N两点.①使点M与点C重合,点N对应的位置标记为点Q.②保持点N不动,将木棒绕点N旋转,使点M落在上,将旋转后点M对应的位置标记为点R.③将延长,在延长线上截取线段 , 得到点S.④作直线 , 即为所求直线.
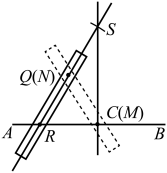 A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行8. 如图,小红家的木门左下角有一点受潮,她想检测门是否变形,准备采用如下方法:先测量门的边和的长,再测量点A和点C间的距离,由此可推断是否为直角,这样做的依据是( )
A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行8. 如图,小红家的木门左下角有一点受潮,她想检测门是否变形,准备采用如下方法:先测量门的边和的长,再测量点A和点C间的距离,由此可推断是否为直角,这样做的依据是( )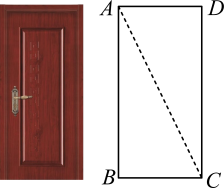 A、勾股定理 B、勾股定理的逆定理 C、三角形内角和定理 D、直角三角形的两锐角互余9. 如图,每个小正方形的边长为1,在中,点D为的中点,则线段的长为( )
A、勾股定理 B、勾股定理的逆定理 C、三角形内角和定理 D、直角三角形的两锐角互余9. 如图,每个小正方形的边长为1,在中,点D为的中点,则线段的长为( )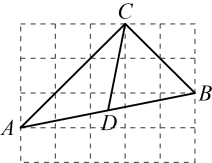 A、 B、 C、 D、10. 如图,在网格中,点A , B , C都是格点(网格线的交点),则的形状是( )
A、 B、 C、 D、10. 如图,在网格中,点A , B , C都是格点(网格线的交点),则的形状是( ) A、等腰直角三角形 B、等腰三角形 C、直角三角形 D、等边三角形
A、等腰直角三角形 B、等腰三角形 C、直角三角形 D、等边三角形二、填空题
-
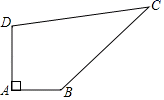
11. 如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入元.
 12. 若a,b,c是直角三角形的三条边长,斜边c上的高的长是h , 给出下列结论:
12. 若a,b,c是直角三角形的三条边长,斜边c上的高的长是h , 给出下列结论:①以a2 , b2 , c2的长为边的三条线段能组成一个三角形;②以 的长为边的三条线段能组成一个三角形;③以a+b , c+h , h的长为边的三条线段能组成直角三角形;④以 的长为边的三条线段能组成直角三角形,符合题意结论的序号为 .
13. 如图,在正方形网格中,每个小正方形的边长都是1,有四条线段,其中能构成直角三角形三边的线段是. 14. 已知等腰的底边 , D是腰上一点,且 , , 则的长为.
14. 已知等腰的底边 , D是腰上一点,且 , , 则的长为. 15. 如图,在正方形网格中,点A,B,C,D,E是格点,则∠ABD+∠CBE的度数为 .
15. 如图,在正方形网格中,点A,B,C,D,E是格点,则∠ABD+∠CBE的度数为 .
三、综合题
-
16. 如图,在中, , , 边上的中线 , 延长至点 , 使 , 连接 .
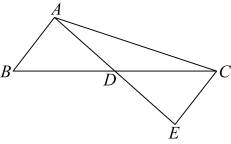 (1)、求证: .(2)、求的长.17. .如图,点在△ABC中, , , , .
(1)、求证: .(2)、求的长.17. .如图,点在△ABC中, , , , . (1)、求BC的长;(2)、求图中阴影部分的面积.18. 在中, , , , 设为最长边,当时,是直角三角形;当时,利用代数式和的大小关系,探究的形状按角分类 .(1)、当三边分别为6、8、9时,为三角形;当三边分别为6、8、11时,为三角形.(2)、猜想,当时,为锐角三角形;当时,为钝角三角形.(3)、判断当 , 时,的形状,并求出对应的的取值范围.19. 课本矩形一节,根据矩形的的性质得到了定理“直角三角形斜边上的中线等于斜边的一半”.
(1)、求BC的长;(2)、求图中阴影部分的面积.18. 在中, , , , 设为最长边,当时,是直角三角形;当时,利用代数式和的大小关系,探究的形状按角分类 .(1)、当三边分别为6、8、9时,为三角形;当三边分别为6、8、11时,为三角形.(2)、猜想,当时,为锐角三角形;当时,为钝角三角形.(3)、判断当 , 时,的形状,并求出对应的的取值范围.19. 课本矩形一节,根据矩形的的性质得到了定理“直角三角形斜边上的中线等于斜边的一半”.小聪同学画出了如图①所示的一个特殊的直角三角形,其中为直角,AD为斜边BC上的中线, . 它证明上面定理思路如下:延长AD至点E,使 , 连结BE,再证 , 从而就可以证明得到;
 (1)、小聪同学还想借助图②,在任意的中,为直角,AD为斜边BC上的中线,证明结论 , 请你帮助小聪同学完成;(2)、如图③,在中 , 垂足为D,如果 , , , 求的中线AE的长度.20. 在学习“勾股数”的知识时,爱动脑的小明设计了如下表格:
(1)、小聪同学还想借助图②,在任意的中,为直角,AD为斜边BC上的中线,证明结论 , 请你帮助小聪同学完成;(2)、如图③,在中 , 垂足为D,如果 , , , 求的中线AE的长度.20. 在学习“勾股数”的知识时,爱动脑的小明设计了如下表格:n
2
3
4
5
6
....
a
4
5
8
10
12
.....
b
3
8
15
24
35
.....
c
5
10
17
26
37
......
请回答下列问题:
(1)、当n=7时,a= , b= , c=;(2)、请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= , b= , c=;(3)、猜想:以a,b,c为边长的三角形是否为直角三角形?并对你的猜想加以证明.