2023-2024学年北师大版数学八年级上册4.4一次函数的应用同步练习(培优卷)
试卷更新日期:2023-08-09 类型:同步测试
一、选择题
-
1. 一次函数( , k、b是常数)与( , m是常数)的图像交于点 , 下列结论正确的序号是( )
①关于的方程的解为;
②一次函数()图像上任意不同两点和满足:;
③若(),则;
④若 , 且 , 则当时, .
A、②③④ B、①②④ C、①②③ D、①②③④2. 如图,在平面直角坐标系中,▱ABCD各顶点的坐标分别为A(1,-1),B(2,-3),C(4,-3),D(3,-1),若直线y=-3x+b与▱ABCD有交点,则b的取值范围是( ) A、3≤b≤8 B、2≤b≤8 C、2≤b≤9 D、-3≤b≤93. 如图,直线y=﹣x+4分别与x轴、y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( )
A、3≤b≤8 B、2≤b≤8 C、2≤b≤9 D、-3≤b≤93. 如图,直线y=﹣x+4分别与x轴、y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( )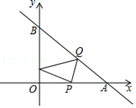 A、(2,2) B、(2.5,1.5) C、(3,1) D、(1.5,2.5)4. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )
A、(2,2) B、(2.5,1.5) C、(3,1) D、(1.5,2.5)4. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )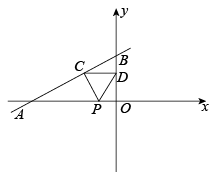 A、 B、 C、 D、5. 小泽和小帅分别从甲地骑自行车沿同一条路到乙地.如图是小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中信息,下列说法有误的是( )
A、 B、 C、 D、5. 小泽和小帅分别从甲地骑自行车沿同一条路到乙地.如图是小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中信息,下列说法有误的是( ) A、从甲到乙地共24千米 B、小帅的骑车速度为8千米/小时 C、小泽出发0.5小时后小帅才出发 D、当小帅到达乙地时,小泽距乙地还有4千米6. 如图,折线表示一骑车人离家的距离 与时间 的关系,骑车人9:00离开家,15:00回到家,则下列说法错误的是( )
A、从甲到乙地共24千米 B、小帅的骑车速度为8千米/小时 C、小泽出发0.5小时后小帅才出发 D、当小帅到达乙地时,小泽距乙地还有4千米6. 如图,折线表示一骑车人离家的距离 与时间 的关系,骑车人9:00离开家,15:00回到家,则下列说法错误的是( )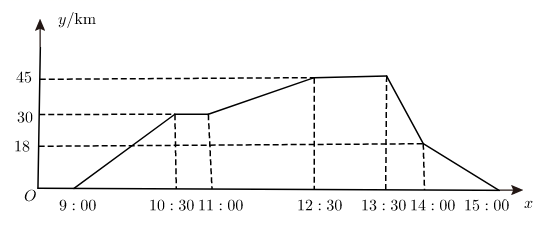 A、骑车人离家最远距离是45km B、骑车人中途休息的总时间长是1.5h C、从9:00到10:30骑车人离家的速度越来越大 D、骑车人返家的平均速度是30km/h7. 如图,在平面直角坐标系中,若折线 与直线交 ( )有且仅有一个交点,则 的取值范围是( )
A、骑车人离家最远距离是45km B、骑车人中途休息的总时间长是1.5h C、从9:00到10:30骑车人离家的速度越来越大 D、骑车人返家的平均速度是30km/h7. 如图,在平面直角坐标系中,若折线 与直线交 ( )有且仅有一个交点,则 的取值范围是( )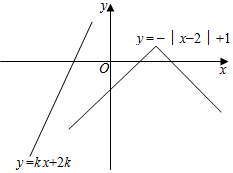 A、 或 B、 或 C、 或 D、 或8. 如图,在Rt△ABO中,∠OAB=90°,B(3,3),点D在边AB上,AD=2BD,点C为OA的中点,点P为边OB上的动点,若四边形PCAD周长最小,则点P的坐标为( )
A、 或 B、 或 C、 或 D、 或8. 如图,在Rt△ABO中,∠OAB=90°,B(3,3),点D在边AB上,AD=2BD,点C为OA的中点,点P为边OB上的动点,若四边形PCAD周长最小,则点P的坐标为( )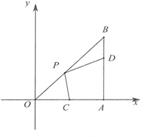 A、( , ) B、(2,2) C、( , ) D、( , )9. 如图,等腰Rt△ABC中,BC= ,以边AC为斜边向右做等腰Rt△ACD,点E是线段CD的中点,连接 AE.作线段CE关于直线AC的对称线段CF,连接BF,并延长BF交线段AE于点G,则线段BG长为( )
A、( , ) B、(2,2) C、( , ) D、( , )9. 如图,等腰Rt△ABC中,BC= ,以边AC为斜边向右做等腰Rt△ACD,点E是线段CD的中点,连接 AE.作线段CE关于直线AC的对称线段CF,连接BF,并延长BF交线段AE于点G,则线段BG长为( ) A、 B、 C、 D、10. 如图,四边形 的顶点坐标分别为 ,当过点 的直线 将四边形 分成面积相等的两部分时,直线 所表示的函数表达式为( )
A、 B、 C、 D、10. 如图,四边形 的顶点坐标分别为 ,当过点 的直线 将四边形 分成面积相等的两部分时,直线 所表示的函数表达式为( )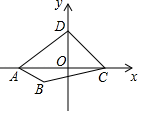 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
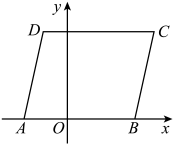
11. 定义:在平面直角坐标系中,若点M关于直线的对称点在的内部(不包含边界),则称点M是关于直线的“伴随点”.如图,已知三点,连接 , 以为边作 . 若在直线上存在点N,使得点N是关于直线的“伴随点”,则n的取值范围是 .
 12. 如图,一次函数的图象分别交x、y轴于点A、B,点P在x轴上,若沿直线将翻折,点O恰好落在直线上的点C处,则点P的坐标是 .
12. 如图,一次函数的图象分别交x、y轴于点A、B,点P在x轴上,若沿直线将翻折,点O恰好落在直线上的点C处,则点P的坐标是 . 13. 如图,一次函数 x+4的图象与x轴交于点A,与y轴交于点B,C是x轴上的一动点,连接BC,将 沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为.
13. 如图,一次函数 x+4的图象与x轴交于点A,与y轴交于点B,C是x轴上的一动点,连接BC,将 沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为. 14. 如图,直线 与两坐标轴分别交于A、B两点,点C是 的中点,点D、E分别是直线 、y轴上的动点,则 的周长最小值是.
14. 如图,直线 与两坐标轴分别交于A、B两点,点C是 的中点,点D、E分别是直线 、y轴上的动点,则 的周长最小值是. 15. 2020年1月15日上午八点,重庆马拉松赛在南滨路鸣枪起跑.为庆祝重马十周年,小明和小红约定一起参加迷你马拉松跑(全长5000 米).比赛开始前,两人约定,完成总路程的 时,速度快的人要在原地停留等待对方.比赛正式开始后,两人均匀速向前.已知小明率先完成全程的 ,并立刻停下,待小红追上时再次以原速匀速出发.一段时间后,小明体力不支,降速为原来的 后匀速前进,最后同时与小红到达终点. 在此过程中,小红速度保持不变.如图是小明和小红之间的距离y(米)与两人出发的时间x(分钟)之间的函数图象.则小明开始降速时,小明距离终点还有米.
15. 2020年1月15日上午八点,重庆马拉松赛在南滨路鸣枪起跑.为庆祝重马十周年,小明和小红约定一起参加迷你马拉松跑(全长5000 米).比赛开始前,两人约定,完成总路程的 时,速度快的人要在原地停留等待对方.比赛正式开始后,两人均匀速向前.已知小明率先完成全程的 ,并立刻停下,待小红追上时再次以原速匀速出发.一段时间后,小明体力不支,降速为原来的 后匀速前进,最后同时与小红到达终点. 在此过程中,小红速度保持不变.如图是小明和小红之间的距离y(米)与两人出发的时间x(分钟)之间的函数图象.则小明开始降速时,小明距离终点还有米.
三、综合题
-
16. 为了响应国家退耕还林政策,某器材销售公司捐出五月份全部销售利润用于种树.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款54万元和其他支出(含人员工资、杂项开支)共3.25万元.这三种器材的进价和售价如下表所示,人员工资(万元)和杂项支出(万元)分别与总销售量x(台)成一次函数关系(如图).

型号
甲
乙
丙
进价(万元/台)
0.9
1.2
1.1
售价(万元/台)
1.2
1.6
1.3
(1)、直接写出:与x之间的函数表达式为;五月份该公司的总销售量为台;(2)、设公司五月份售出甲种型号器材t台,五月份总销售利润为W(万元),求W与t之间的函数表达式;(3)、请推测该公司这次活动捐款金额的最大值.17. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段表示货车离甲地的距离(千米)与时间(小时)之间的函数关系:线段表示轿车离甲地的距离(千米)与时间(小时)之间的函数关系.点在线段上,请根据图象解答下列问题. (1)、轿车的速度是千米/小时;(2)、求轿车出发后、轿车离甲地的距离千米)与时间(小时)之间的函数关系式;(3)、在轿车行驶的过程中,轿车与货车之间的距离为20千米时,直接写出的值.18. 近几年,我国快递市场跟随电商经历了爆发式增长,快递已成为人们生活的一部分.越来越多的人选择通过快递公司代办点邮寄包裹,那么选择哪家快递公司更合算呢?以此为驱动问题,某校八年级开展了项目学习.如表是李华同学帮家人选择更优惠的快递公司的活动报告(不完整),请仔细阅读并完成相应任务.
(1)、轿车的速度是千米/小时;(2)、求轿车出发后、轿车离甲地的距离千米)与时间(小时)之间的函数关系式;(3)、在轿车行驶的过程中,轿车与货车之间的距离为20千米时,直接写出的值.18. 近几年,我国快递市场跟随电商经历了爆发式增长,快递已成为人们生活的一部分.越来越多的人选择通过快递公司代办点邮寄包裹,那么选择哪家快递公司更合算呢?以此为驱动问题,某校八年级开展了项目学习.如表是李华同学帮家人选择更优惠的快递公司的活动报告(不完整),请仔细阅读并完成相应任务.为家人选择更优惠的快递公司活动报告
⑴收集信息
经了解我家附近有甲、乙两个不同的快递公司代办点,服务质量同等,爸爸妈妈邮寄快递通常是随机去其中的一个代办点,他们邮寄的快递都是省外且在10kg以内,体积一般较小.
快递费通常是由首重费和续重费组成,以1kg为单位计费,不足1kg按1kg计费.取实际重量和体积重量(长×宽×高/6000,单位cm)中两者较大值作为物品重量计费.
甲、乙两个代办点省外邮寄费用标准如下:
甲:首重1kg收费8元,续重5元/kg;(即所寄物品重量不超过1kg时收费8元,重量超过1kg时超过部分按每千克加收5元计费)
乙:首重1kg收费10元,续重4元/kg.
⑵建立模型
①发现所寄物品的快递费用y(元)与物品重量x(kg)之间存在函数关系,y与x之间的关系式为:
, .
②在同一平面直角坐标系内画出两个函数的图象(如图,不完整),两图象交于点A.

⑶解决问题
我们可以根据图象推断哪个快递公司更优惠,结论如下:
任务:
(1)、直接将函数图象补充完整(在图中画出y乙函数图象)(不需要过程).(2)、写出点A的坐标,并解释该点坐标所表示的实际意义.(3)、根据图象推断哪个快递公司更优惠.19. 定义:对于给定的一次函数( , k、b为常数),把形如( , k、b为常数)的函数称为一次函数( , k、b为常数)的衍生函数.已知的顶点坐标分别为 , , , . (1)、点在一次函数的衍生函数图象上,则;(2)、如图,一次函数( , k、b为常数)的衍生函数图象与交于M、N、P、Q四点,其中P点坐标是 , 并且 , 求该一次函数的解析式.(3)、一次函数( , k、b为常数),其中k、b满足 .
(1)、点在一次函数的衍生函数图象上,则;(2)、如图,一次函数( , k、b为常数)的衍生函数图象与交于M、N、P、Q四点,其中P点坐标是 , 并且 , 求该一次函数的解析式.(3)、一次函数( , k、b为常数),其中k、b满足 .①请问一次函数的图象是否经过某个定点,若经过,请求出定点坐标;若不经过,请说明理由;
②一次函数( , k、b为常数)的衍生函数图象与恰好有两个交点,求b的取值范围.
20. 某动力科学研究院实验基地内装有一段笔直的轨道 , 长度为的金属滑块在上面做往返滑动.如图,滑块首先沿方向从左向右匀速滑动,滑动速度为 , 滑动开始前滑块左端与点重合,当滑块右端到达点时,滑块停顿 , 然后再以小于的速度匀速返回,直到滑块的左端与点重合,滑动停止.设时间为时,滑块左端离点的距离为 , 右端离点的距离为 , 记与具有函数关系.已知滑块在从左向右滑动过程中,当和时,与之对应的的两个值互为相反数;滑块从点出发到最后返回点 , 整个过程总用时(含停顿时间).请你根据所给条件解决下列问题: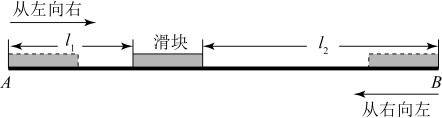 (1)、滑块从点到点的滑动过程中,的值;(填“由负到正”或“由正到负”)(2)、滑块从点到点的滑动过程中,求与的函数表达式;(3)、在整个往返过程中,若 , 求的值.
(1)、滑块从点到点的滑动过程中,的值;(填“由负到正”或“由正到负”)(2)、滑块从点到点的滑动过程中,求与的函数表达式;(3)、在整个往返过程中,若 , 求的值.