2023-2024学年北师大版数学八年级上册4.4一次函数的应用同步练习（提升卷）

试卷更新日期：2023-08-09 类型：同步测试

进入出卷网下载

一、选择题

1. 在平面直角坐标系xOy中，已知直线l经过二、三、四象限，且还经过点 $(0 ， m)$ ， $(2 ， n)$ ， $(p ， 1)$ 和 $(3 ， - 2)$ ，则下列判断正确的是（）

A、 $m < n$ B、 $m < - 3$ C、 $n < - 2$ D、 $p < - 1.5$

查看试题解析
2. 直线 $y = m x - 2$ 和 $y = n x - 6$ 相交于x轴上同一点，则 $\frac{m}{n}$ 的值为（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、-3

查看试题解析
3. 在直角坐标系中，已知点 $A (\frac{\sqrt{7}}{2} ， m)$ ，点 $B (\frac{3}{2} ， n)$ 是直线 $y = k x + b (k < 0)$ 上的两点，则 $m ， n$ 的大小关系是（）

A、 $m \leq n$ B、 $m \geq n$ C、 $m < n$ D、 $m > n$

查看试题解析
4. 点A(-2，y₁)，B(3，y₂)在一次函数 $y = x + b$ 的图象上，y₁与y₂的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、 $y_{1} \geq y_{2}$

查看试题解析
5. 已知直线 $y = 3 x$ 与 $y = - 2 x + b$ 的交点的坐标为 $(1 ， a)$ ，则a+b的值为（）

A、2 B、4 C、8 D、15

查看试题解析
6. 在直角坐标系中，已知点 $A (\frac{3}{2} ， m)$ ，点 $B (\frac{\sqrt{7}}{2} ， n)$ 是直线 $y = k x + b (k < 0)$ 上的两点，则 $m$ ， $n$ 的大小关系是（）

A、 $m < n$ B、 $m > n$ C、 $m \geq n$ D、 $m \leq n$

查看试题解析
7. 如图，在平面直角坐标系中，直线 $y = \frac{4}{3} x + 4$ 与x轴交于点A，与y轴交于点B，直线 $y = - 4 x + 4$ 与x轴交于点C，与y轴交于点B，若线段 $B C$ 上的点D到直线 $A B$ 的距离 $D E$ 长为3，则点D的坐标为（）

A、 $(\frac{15}{16} ， \frac{1}{4})$ B、 $(\frac{31}{32} ， \frac{1}{8})$ C、 $(\frac{3}{4} ， 1)$ D、 $(\frac{5}{6} ， \frac{2}{3})$

查看试题解析
8. 如图，在平面直角坐标系中，直线 $a ， b$ 相交于点 $C (- \frac{1}{2} ， \frac{\sqrt{3}}{2})$ ， $O A = O B = 1$ ．下列四个说法：
$① a ⊥ b$ ；
$②$ $C$ 为线段 $B D$ 中点；
$③$ $△ A B C ≌ △ B O D$ ；
$④$ 点E的坐标为 $(0 ， \frac{\sqrt{3}}{3})$ ．其中正确说法的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
9. 弹簧的长度与所挂物体的质量的关系为一次函数，如图所示，由此图可知不挂物体时弹簧的长度为（）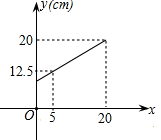

A、7cm B、8cm C、9cm D、10cm

查看试题解析
10. 如图，直线 $y_{1} = a x (a \neq 0)$ 与 $y_{2} = \frac{1}{2} x + b$ 交于点 $P$ ，有四个结论：① $a < 0$ ；② $b < 0$ ；③当 $x > 0$ 时， $y_{1} > 0$ ；④当 $x < - 2$ 时， $y_{1} > y_{2}$ ，其中正确的是（）

A、①② B、①③ C、①④ D、②④

查看试题解析

二、填空题

11. 如图，直线 $y = k x + 2$ 与x轴，y轴分别交于A，C两点，点B与点A关于y轴对称，连接 $B C$ ， $B C = 2 \sqrt{5}$ ，点M，N分别是线段 $A B ， A C$ 上的动点（M不与A，B重合），且满足 $∠ C M N = ∠ C B A$ .当 $△ C M N$ 为等腰三角形时，M的坐标为.

查看试题解析
12. 直线 $y = - 2 x + b$ 经过点 $(m ， y_{1})$ ， $(m - 4 ， y_{2})$ ，则 $y_{1}$ $y_{2}$ （填“ $<$ ”或“ $>$ ”）.

查看试题解析
13. 已知 $(- 2 ， y_{1})$ ， $(1 ， y_{2})$ 是直线 $y = - \frac{2}{3} x + b$ （b为常数）上的两个点，则 $y_{1}$ $y_{2}$ （填入“<”、“=”或“>”）.

查看试题解析

14. 某种气体的体积y (L)与气体的温度x (C)对应值如下表．若要使气体的体积至少为106升，则气体的温度不低于℃．

x(℃)	……	0	1	2	3	……	10	……
y(L)	……	100	100.3	100.6	100.9	……	103	……

查看试题解析

15. 如图，直线 $y = \frac{4}{3} x + 8$ 与x轴、y轴分别交于点B和点A，点C是线段 $O A$ 上的一点，若将 $△ A B C$ 沿 $B C$ 折叠，点A恰好落在x轴上的 $A ′$ 处，若P是y轴负半轴上一动点，且 $△ B C P$ 是等腰三角形，则P的坐标为．

查看试题解析

三、综合题

16. 如图，大拇指与小拇指尽量张开时，两指尖的距离称为“指距”，研究表明，一般情况下人的身高 $h (c m)$ 是指距 $d (c m)$ 的一次函数，
【测量数据】测量数据如表：
指距 $d (c m)$
20
21
22
23
身高 $h (c m)$
160
169
178
187

(1)、【关系探究】
根据表中数据，求h与d之间的函数关系式；

(2)、【结论应用】
我国篮球运动员周琦的身高约为 $217 c m$ ，估算他的指距是多少？（结果精确到 $0.1 c m$ ）

查看试题解析
17. 如图，欣欣妈妈在超市购买某种水果所付金额 $y$ （元）与购买 $x$ （千克）之间的函数图象如图所示，

(1)、求 $x \geq 4$ 时， $y$ 与 $x$ 之间的函数关系；

(2)、请你帮欣欣妈妈计算：一次性购买 $6$ 千克这种水果比平均分 $2$ 次购买可节省多少元？

查看试题解析
18. 小亮和小刚进行赛跑训练，他们选择了一个土坡，按同一路线同时出发，从坡底跑到坡顶再原路返回坡底.他们俩上坡的平均速度不同，下坡的平均速度则是各自上坡平均速度的 $1.5$ 倍.设两人出发 $x m i n$ 后距出发点的距离为 $y m$ .图中折线表示小亮在整个训练中 $y$ 与 $x$ 的函数关系，其中 $A$ 点在 $x$ 轴上， $M$ 点坐标为 $(4 ， 0)$ .

(1)、小亮下披的速度是 $m / m i n$

(2)、求出 $A B$ 所在直线的函数关系式；

查看试题解析
19. 甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同.“五一”假期，两家均推出了优惠方案，甲采摘园的优惠方案：游客进园需购买60元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案：游客进园不需购买门票，采摘的草莓超过一定数量后，超过部分打折优惠.优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为 $y_{甲}$ (元），在乙采摘园所需总费用为 $y_{乙}$ (元），图中折线 $O － A － B$ 表示 $y_{乙}$ 与x之间的函数关系.

(1)、求 $y_{甲}$ 与x之间的函数关系式、 $y_{乙}$ 与x（只求 $x \geq 10$ 时直线 $A B$ ）的函数关系式；

(2)、当游客采摘15千克的草莓时，你认为他在哪家草莓园采摘更划算？

查看试题解析
20. A，B两地之间有一条长为600千米的公路，甲乙两车都从A地匀速开往B地，乙车先出发，然后甲车再出发，两车分别到达目的地后停止，已知甲乙两车相距的路程y（千米）与乙车行驶的时间x（时）之间的函数关系如图所示.

(1)、甲的速度为千米/时，乙的速度为千米/时.

(2)、求直线 $R S$ 的函数表达式.

(3)、当甲车与乙车相距的路程为80千米时，求此时乙车行驶的时间.

查看试题解析

指距 $d (c m)$	20	21	22	23
身高 $h (c m)$	160	169	178	187