2023年浙教版数学九年级上册1.4 二次函数的应用同步测试（基础版）

试卷更新日期：2023-08-09 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 二次函数 $y = x^{2} - 3 x + 1$ 的图象与y轴的交点坐标是（）

A、 $(0 ， 0)$ B、 $(0 ， 1)$ C、 $(0 ， - 3)$ D、 $(3 ， 0)$

查看试题解析
2. 抛物线 $y = x^{2} - 2 x$ 的图象与x轴交点的横坐标分别是（）

A、0，1 B、1，2 C、0，2 D、－1，－2

查看试题解析
3. 根据以下表格中二次函数y＝ax²+bx+c的自变量x与函数值y的对应值，可以判断方程ax²+bx+c＝0的一个解x的范围是（）

x

0

0.5

1

1.5

2

y＝ax²+bx+c

﹣1

﹣0.5

1

3.5

7

A、0＜x＜0.5 B、0.5＜x＜1 C、1＜x＜1.5 D、1.5＜x＜2

查看试题解析
4. 已知二次函数 $y = a x^{2} + b x + c$ ，函数值 $y$ 与自变量 $x$ 的部分对应值如表：
$x$
$\dots$
-1
0
1
2
3
$\dots$
$y$
$\dots$
18
8
2
0
2
$\dots$
则当 $y > 8$ 时， $x$ 的取值范围是（）

A、 $0 < x < 4$ B、 $0 < x < 5$ C、 $x < 0$ 或 $x > 4$ D、 $x < 0$ 或 $x > 5$

查看试题解析
5. 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）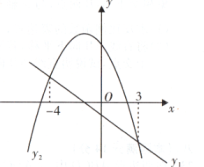

A、-4<x<3 B、x<-4 C、3-<<x<-4 D、x>3或x<-4

查看试题解析
6. 如图，一个矩形的长比宽多3cm，矩形的面积是Scm² ．设矩形的宽为xcm，当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数关系是（）

A、S=4x+6 B、S=4x-6 C、S=x²+3x D、S=x²-3x

查看试题解析
7. 正方体的棱长为x，表面积为y，则y与x之间的函数关系式为（）

A、 $y = \frac{1}{6} x$ B、 $y = 6 x$ C、 $y = 6 x^{2}$ D、 $y = \frac{6}{x}$

查看试题解析
8. 将进货价格为35元的商品按单价40元售出时，能卖出200个.已知该商品单价每上涨1元，其销售量就减少5个.设这种商品的售价上涨x元时，获得的利润为y元，则下列关系式正确的是（）

A、y＝（x-35）（200-5x） B、y＝（x+40）（200−10x） C、y＝（x+5）（200-5x） D、y＝（x+5）（200−10x）

查看试题解析
9. 某种商品每天的销售利润y（元）与单价x（元）之间的函数关系式为 $y = - 0.1 {(x - 3)}^{2} + 25$ ．则这种商品每天的最大利润为（）

A、0.1元 B、3元 C、25元 D、75元

查看试题解析
10. 如图，从地面竖直向上抛出一个小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的关系式为h＝30t-5t² ，那么小球从抛出至回落到地面所需要的时间是（　　）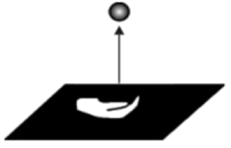

A、6s B、4s C、3s D、2s

查看试题解析

二、填空题（每空4分，共24分）

11. 抛物线 $y = - x^{2} + x - 3$ 与y轴的交点坐标是．

查看试题解析
12. 如图，抛物线 $y = a x^{2} + b x + c$ （ $a$ ， $b$ ， $c$ 为常数，且 $a \neq 0$ ）交 $x$ 轴于 $A (- 1 ， 0)$ ， $B (2 ， 0)$ 两点，则不等式 $x^{2} + \frac{b}{a} x + \frac{c}{a} > 0$ 的解为.

查看试题解析
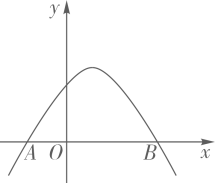13. 抛物线y=x²+8x﹣4与直线x=﹣4的交点坐标是．

查看试题解析
14. 用长12m的铝合金条制成矩形窗框（如图所示），那么这个窗户的最大透光面积是（中间横框所占的面积忽略不计）

查看试题解析
15. 某件商品的销售利润y（元）与商品单价x（元）之间满足 $y = - x^{2} + 6 x - 7$ ，不考虑其他因素，该商品的单价定为元时，销售一件该商品获得的利润最大，最大利润为元．

查看试题解析
16. 教练对小明推铅球的录像进行技术分析，建立平面直角坐标系（如图），发现铅球与地面的高度 $y (m)$ 和运动员出手点的水平距离 $x (m)$ 之间的函数关系为 $y = - \frac{1}{10} x^{2} + \frac{4}{5} x + 2$ ，由此可知铅球的落地点与运动员出手点的水平距离是m.

查看试题解析

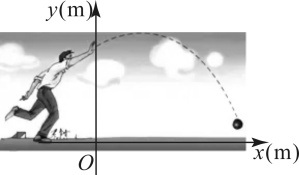
三、解答题（共8题，共66分）

17. 一元二次方程x²+7x+9=1的根与二次函数y=x²+7x+9的图象有什么关系？试把方程的根在图象上表示出来．

查看试题解析
18. 指出抛物线 $y = 3 x^{2} - 6 x - 9$ 的开口方向：写出抛物线的顶点坐标、对称轴方程；当x满足什么条件时，y随x的增大而增大大？当x满足什么条件时，y取最小值多少？当x满足什么条件时， $y < 0$ ？当x满足什么条件时， $y > 0$ ？

查看试题解析
19. 抛物线 $y = 3 x^{2}$ 与直线y＝kx+3的交点为（2，b），求k和b．

查看试题解析
20. 已知抛物线 $y = - x^{2} + 4 x + 5$ .

(1)、求抛物线与y轴交点的坐标；

(2)、求抛物线的对称轴.

查看试题解析
21. 一运动员推铅球，铅球经过的路线为如图所示的抛物线.求铅球的落地点离运动员有多远（结果保留根号）？

查看试题解析
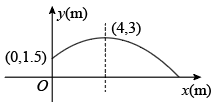22. 如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线．若不考虑空气阻力，小球的飞行高度h(单位：m)与飞行时间t(单位：s)之间具有函数关系：h=-5t²+20t，求小球飞行高度达到最高时的飞行时间．

查看试题解析
23. 商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施，经调查发现，每件商品每降价1元，商场每天可多售出2件，设每件商品降低x元据此规律，请回答：

(1)、商场日销售量增加件，每件商品盈利元（用含x的代数式表示）；

(2)、在上述条件不变，销售正常的情况下，设商场日盈利y元，求y与x的函数关系式；

(3)、在（2）的条件下，每件商品降价多少元时，商场日盈利最高？

查看试题解析
24. 某花圃销售一批名贵花卉，平均每天可售出20盆，每盆盈利40元，为了增加盈利并尽快减少库存，花圃决定采取适当的降价措施，经调查发现，如果每盆花卉每降1元，花圃平均每天可多售出2盆．

(1)、若花圃平均每天要盈利1200元，每盆花卉应降价多少元？

(2)、每盆花卉降低多少元时，花圃平均每天盈利最多，是多少？

查看试题解析

x	0	0.5	1	1.5	2
y＝ax²+bx+c	﹣1	﹣0.5	1	3.5	7

$x$	$\dots$	-1	0	1	2	3	$\dots$
$y$	$\dots$	18	8	2	0	2	$\dots$

2023年浙教版数学九年级上册1.4 二次函数的应用 同步测试（基础版）

一、选择题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学九年级上册1.4 二次函数的应用同步测试（基础版）