2023年浙教版数学九年级上册1.3 二次函数的性质 同步测试(培优版)
试卷更新日期:2023-08-09 类型:同步测试
一、选择题(每题3分, 共30分)
-
1. 如图,在平面直角坐标系中,直线与抛物线相交于点 , . 结合图象,判断下列结论:①当时,;②是方程的一个解;③若 , 是抛物线上的两点,则;④对于抛物线, , 当时,的取值范围是 . 其中正确结论的个数是( )
 A、4个 B、3个 C、2个 D、1个2. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②方程()必有一个根大于2且小于3;③若是抛物线上的两点,那么;④;⑤对于任意实数m,都有 , 其中正确结论的个数是( )
A、4个 B、3个 C、2个 D、1个2. 二次函数的图象如图所示,对称轴是直线 , 下列结论:①;②方程()必有一个根大于2且小于3;③若是抛物线上的两点,那么;④;⑤对于任意实数m,都有 , 其中正确结论的个数是( ) A、5 B、4 C、3 D、23. 如图,是线段上一点,和是位于直线同侧的两个等边三角形,点分别是的中点.若 , 则下列结论错误的是( )
A、5 B、4 C、3 D、23. 如图,是线段上一点,和是位于直线同侧的两个等边三角形,点分别是的中点.若 , 则下列结论错误的是( )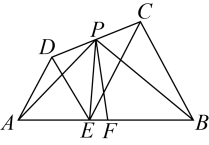 A、的最小值为 B、的最小值为 C、周长的最小值为6 D、四边形面积的最小值为4. 已知抛物线是常数开口向下,过 , 两点,且下列四个结论:
A、的最小值为 B、的最小值为 C、周长的最小值为6 D、四边形面积的最小值为4. 已知抛物线是常数开口向下,过 , 两点,且下列四个结论:若 , 则;
若时,则;
若点 , , 在抛物线上, , 且 , 则;
当时,关于x的一元二次方程必有两个不相等的实数根.
如果 , , 那么当时,直线与该二次函数有一个公共点,则 . 其中结论正确的个数有( )
A、个 B、个 C、个 D、个5. 规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点为整点.对于题目:抛物线与轴分别交于、两点(点M在点N的左侧), , 线段与抛物线围成的封闭区域记作(包括边界),若区域内有6个整点,求的取值范围.则( )A、 B、 C、或 D、或6. 如图所示是抛物线的部分图象,其顶点坐标为 , 且与x轴的一个交点在点和之间,则下列结论:①;②;③;④一元二次方程没有实数根.其中正确的结论个数是( ) A、1个 B、2个 C、3个 D、4个7. 如图,抛物线y=ax2+bx+c的顶点坐标为(1,n).下列结论:①abc<0;②8a+c<0;③关于x的一元二次方程ax2+bx+c=n-1有两个不相等实数根;④抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2 . 其中正确的结论共有( )
A、1个 B、2个 C、3个 D、4个7. 如图,抛物线y=ax2+bx+c的顶点坐标为(1,n).下列结论:①abc<0;②8a+c<0;③关于x的一元二次方程ax2+bx+c=n-1有两个不相等实数根;④抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2 . 其中正确的结论共有( ) A、1个 B、2个 C、3个 D、4个8. 已知二次函数y=(x-m+2)(x+m-4)+n,其中m,n为常数,则( )A、m>1,n<0时,二次函数的最小值大于0 B、m=1,n>0时,二次函数的最小值大于0 C、m<1,n>0时,二次函数的最小值小于0 D、m=1,n<0时,二次函数的最小值小于09. 如图,抛物线与x轴相交于点 , , 与y轴相交于点C,甲、乙、丙、丁四名同学在一起探究该函数的图象与性质,下面是他们得出的结论,其中正确的个数是( )
A、1个 B、2个 C、3个 D、4个8. 已知二次函数y=(x-m+2)(x+m-4)+n,其中m,n为常数,则( )A、m>1,n<0时,二次函数的最小值大于0 B、m=1,n>0时,二次函数的最小值大于0 C、m<1,n>0时,二次函数的最小值小于0 D、m=1,n<0时,二次函数的最小值小于09. 如图,抛物线与x轴相交于点 , , 与y轴相交于点C,甲、乙、丙、丁四名同学在一起探究该函数的图象与性质,下面是他们得出的结论,其中正确的个数是( ) A、1 B、2 C、3 D、410. 已知非负数 , 满足且 , 设的最大值为 , 最小值为 , 则的值是( )A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、410. 已知非负数 , 满足且 , 设的最大值为 , 最小值为 , 则的值是( )A、1 B、2 C、3 D、4二、填空题(每空3分,共21分)
-
11. 定义:若x,y满足且(t为常数),则称点为“和谐点”.(1)、若是“和谐点”,则 .(2)、若双曲线存在“和谐点”,则k的取值范围为 .12. 已知抛物线(a,b,c是常数,),且 , . 下列四个结论:
①对于任意实数 , 恒成立;
②若 , 则不等式的解集是;
③一元二次方程有一个根;
④点 , 在抛物线上,若 , 则当时,总有 . 其中正确的是 . (填写序号)
13. 已知二次函数y=x2+bx+c.当-1≤x≤1时,y的取值范围是-1≤y≤1,该二次函数的对称轴为x=m,则m的值是.14. 已知关于的二次函数 , 其中为实数,当-2≤x≤1时,的最小值为4,满足条件的的值为。15. 如图,在平面直角坐标系xOy中,抛物线y=-x2+6x+c的对称轴与x轴交于点A,在直线AB:y=kx+3上取一点B,使点B在第四象限,且到两坐标轴的距离和为7,设P是抛物线的对称轴上的一点,点Q在抛物线上,若以点A,B,P,Q为顶点的四边形为正方形,则c的值为 .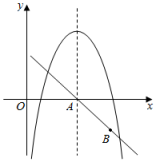 16. 已知抛物线y=x2+4x-8与直线l交(抛物线)于点A(-5,m),B(n,-3)(n>0).若点P在抛物线上且在直线l下方(不与点A,B重合),则点P的纵坐标的取值范围为 .
16. 已知抛物线y=x2+4x-8与直线l交(抛物线)于点A(-5,m),B(n,-3)(n>0).若点P在抛物线上且在直线l下方(不与点A,B重合),则点P的纵坐标的取值范围为 .三、解答题(共8题,共69分)
-
17. 如图,在平面直角坐标系中,已知二次函数的图象与x轴交于点和点两点,与y轴交于点 . 点D为线段上的一动点.
 (1)、求二次函数的表达式;(2)、如图1,求周长的最小值;(3)、如图2,过动点D作交抛物线第一象限部分于点P,连接 , 记与的面积和为S,当S取得最大值时,求点P的坐标,并求出此时S的最大值.18. 如图,直线交轴于点 , 交轴于点 , 对称轴为的抛物线经过两点,交轴负半轴于点 . 为抛物线上一动点,点的横坐标为 , 过点作轴的平行线交抛物线于另一点 , 作轴的垂线 , 垂足为 , 直线交轴于点 .
(1)、求二次函数的表达式;(2)、如图1,求周长的最小值;(3)、如图2,过动点D作交抛物线第一象限部分于点P,连接 , 记与的面积和为S,当S取得最大值时,求点P的坐标,并求出此时S的最大值.18. 如图,直线交轴于点 , 交轴于点 , 对称轴为的抛物线经过两点,交轴负半轴于点 . 为抛物线上一动点,点的横坐标为 , 过点作轴的平行线交抛物线于另一点 , 作轴的垂线 , 垂足为 , 直线交轴于点 .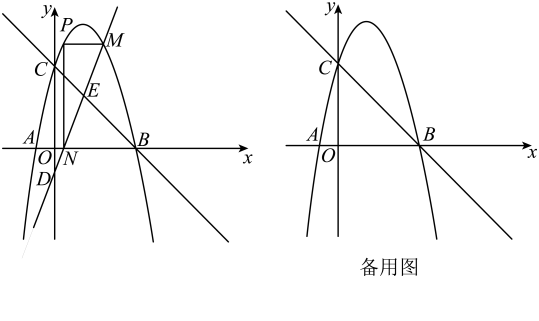 (1)、求抛物线的解析式;(2)、若 , 当为何值时,四边形是平行四边形?(3)、若 , 设直线交直线于点 , 是否存在这样的值,使?若存在,求出此时的值;若不存在,请说明理由.19. 如图,抛物线过点 , , 矩形的边在线段上(点B在点A的左侧),点C,D在抛物线上,设 , 当时, .
(1)、求抛物线的解析式;(2)、若 , 当为何值时,四边形是平行四边形?(3)、若 , 设直线交直线于点 , 是否存在这样的值,使?若存在,求出此时的值;若不存在,请说明理由.19. 如图,抛物线过点 , , 矩形的边在线段上(点B在点A的左侧),点C,D在抛物线上,设 , 当时, . (1)、求抛物线的函数表达式;(2)、当t为何值时,矩形的周长有最大值?最大值是多少?(3)、保持时的矩形不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G,H,且直线平分矩形的面积时,求抛物线平移的距离.20. 如图,在平面直角坐标系中,抛物线交轴于点 , 顶点坐标为 . 抛物线交轴于点 , 顶点坐标为 .
(1)、求抛物线的函数表达式;(2)、当t为何值时,矩形的周长有最大值?最大值是多少?(3)、保持时的矩形不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G,H,且直线平分矩形的面积时,求抛物线平移的距离.20. 如图,在平面直角坐标系中,抛物线交轴于点 , 顶点坐标为 . 抛物线交轴于点 , 顶点坐标为 . (1)、连接 , 求线段的长;(2)、点在抛物线上,点在抛物线上.比较大小:;(3)、若点在抛物线上, , 求的取值范围.21. 如图,在平面直角坐标系中,抛物线经过点 . 点 , 在此抛物线上,其横坐标分别为 , 连接 , .
(1)、连接 , 求线段的长;(2)、点在抛物线上,点在抛物线上.比较大小:;(3)、若点在抛物线上, , 求的取值范围.21. 如图,在平面直角坐标系中,抛物线经过点 . 点 , 在此抛物线上,其横坐标分别为 , 连接 , .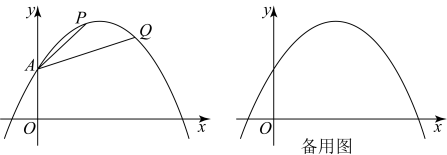 (1)、求此抛物线的解析式.(2)、当点与此抛物线的顶点重合时,求的值.(3)、当的边与轴平行时,求点与点的纵坐标的差.(4)、设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为 , 在点与点之间部分(包括点和点)的最高点与最低点的纵坐标的差为 . 当时,直接写出的值.22. 如图,抛物线:与轴交于、两点(点在点的左侧),与轴交于点且 , 点为抛物线的对称轴右侧图象上的一点(不含顶点).
(1)、求此抛物线的解析式.(2)、当点与此抛物线的顶点重合时,求的值.(3)、当的边与轴平行时,求点与点的纵坐标的差.(4)、设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为 , 在点与点之间部分(包括点和点)的最高点与最低点的纵坐标的差为 . 当时,直接写出的值.22. 如图,抛物线:与轴交于、两点(点在点的左侧),与轴交于点且 , 点为抛物线的对称轴右侧图象上的一点(不含顶点).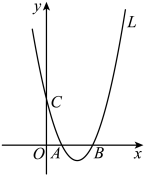 (1)、的值为 , 抛物线的顶点坐标为;(2)、设抛物线在点和点之间的部分(含点和点)的最高点与最低点的纵坐标之差为 , 求关于的函数表达式,并写出自变量的取值范围;(3)、若点的坐标满足时,连接 , 将直线与抛物线围成的封闭图形记为 .
(1)、的值为 , 抛物线的顶点坐标为;(2)、设抛物线在点和点之间的部分(含点和点)的最高点与最低点的纵坐标之差为 , 求关于的函数表达式,并写出自变量的取值范围;(3)、若点的坐标满足时,连接 , 将直线与抛物线围成的封闭图形记为 .①求点的坐标;
②直接写出封闭图形的边界上的整点(横、纵坐标都是整数)的个数.
