2023年浙教版数学九年级上册1.2 二次函数的图象同步测试（提高版）

试卷更新日期：2023-08-09 类型：同步测试

进入出卷网下载

一、选择题

1. 若函数 $y = a x^{a^{2} - 2 a - 6}$ 是二次函数且图像开口向上，则a=（）

A、﹣2 B、4 C、4或﹣2 D、4或3

查看试题解析
2. 一次函数 $y = k x + k$ 与二次函数 $y = a x^{2}$ 的图象如图所示，那么二次函数 $y = a x^{2} - k x - k$ 的图象可能为（）

A、 B、 C、 D、

查看试题解析
3. 下列抛物线中，与抛物线y=2(x-1)²+2形状相同的是（）

A、y= $\frac{1}{2}$ (x-1)² B、y=2x² C、y=(x-1)²+2 D、y=(2x-1)²+2

查看试题解析
4. 对于二次函数y=(x-4)²+2的图象，下列说法正确的是（）

A、开口向下 B、对称轴是直线x=2 C、顶点坐标是（4，2） D、与x轴有两个交点

查看试题解析
5. 二次函数 $y = m x^{2} - 2 m^{2} x + n$ 图象经过点 $A (- 3 ， y_{1})$ ， $B (7 ， y_{2})$ ，且 $y_{1} > y_{2}$ ，则m的取值范围是（）

A、 $0 < m < 2$ B、 $m < 0$ 或 $m>2$ C、 $- 3 < m < 0$ D、 $m < - 3$ 或 $m > 7$

查看试题解析
6. 设二次函数 $y = x^{2} - k x + 2 k$ （ $k$ 为实数）的图象过点 $(1 ， y_{1})$ ， $(2 ， y_{2})$ ， $(3 ， y_{3})$ ， $(4 ， y_{4})$ ，设 $y_{1} - y_{2} = a$ ， $y_{3} - y_{4} = b$ ，（）

A、若 $a b < 0$ ，且 $a + b < 0$ ，则 $k < 3$ B、若 $a b < 0$ ，且 $a + b > 0$ ，则 $k < 5$ C、若 $a b > 0$ ，且 $a + b < 0$ ，则 $k > 3$ D、若 $a b > 0$ ，且 $a + b > 0$ ，则 $k > 7$

查看试题解析
7. 将二次函数y＝x²-4x+8转化为y＝a（x-m）²+k的形式，其结果为（）

A、y＝（x-2）²+4 B、y＝（x+4）²+4 C、y＝（x-4）²+8 D、y＝（x-2）²-4

查看试题解析
8. 抛物线 $y = x^{2} - 2 x - 1$ 的图象向左平移2个单位，再向上平移3个单位，所得图象的解析式为（）

A、 $y = x^{2} - 6 x + 10$ B、 $y = x^{2} + 2 x + 2$ C、 $y = x^{2} - 6 x + 4$ D、 $y = x^{2} - 2 x - 4$

查看试题解析
9. 要将抛物线 $y = - 3 x^{2}$ 平移后得到抛物线 $y = - 3 {(x + 1)}^{2} + 3$ ，下列平移方法正确的是（）

A、向左平移1个单位，再向上平移3个单位 B、向左平移1个单位，再向下平移3个单位 C、向右平移1个单位，再向上平移3个单位 D、向右平移1个单位，再向下平移3个单位

查看试题解析
10. 如图，在平面直角坐标系xOy中，点A，B，C的坐标满足二次函数y=ax²+bx(a≠0)的表达式，则对该二次函数的系数a和b判断正确的是（）

A、a<0，b>0 B、a<0，b<0 C、a>0，b<0 D、a>0，b>0

查看试题解析

二、填空题

11. 二次函数 $y = {(x - 2)}^{2} + h (b \leq x \leq b + 1)$ 的图象上任意二点连线不与 $x$ 轴平行，则 $b$ 的取值范围为.

查看试题解析
12. 点 $P (2 ， 9)$ 为二次函数 $y = a x^{2} + 6 a x + 5$ 图象上一点，其对称轴为 $l$ ，则点 $P$ 关于 $l$ 的对称点的坐标为.

查看试题解析
13. 将二次函数 $y = {(x - 1)}^{2} + 2$ 向左平移4个单位，向下平移2个单位，所得到的新函数关系式为.

查看试题解析
14. 若将抛物线y＝x²-6x+5所在的平面直角坐标系中的x轴向上平移1个单位，把y轴向右平移2个单位，则该抛物线在新的平面直角坐标系下的函数表达式为．

查看试题解析
15. 在平面直角坐标系xOy中，将二次函数y＝ax²－4ax＋c(a为常数，且a＜0)的图象沿着y轴向下平移，交x轴于O，A两点，则OA的长为．

查看试题解析
16. 如图，已知抛物线y＝ax²+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y＝a₁x²+b₁x+c₁ ，则下列结论正确的是．（写出所有正确结论的序号）

①b＞0

②a﹣b+c＜0

③阴影部分的面积为4

④若c＝﹣1，则b²＝4a ．

查看试题解析

三、综合题

17. 如图，已知二次函数y=ax²+bx+c的图象过A（2，0），B（0，﹣1）和C（4，5）三点.

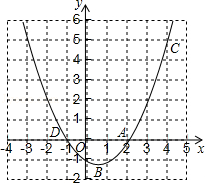(1)、求二次函数的解析式；

(2)、在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值.

查看试题解析
18. 已知拋物线 $y = a x^{2} + b x + c$ 经过点 $(1 ， 0)$ ．

(1)、如果此抛物线同时经过 $(3 ， 0)$ ，求抛物线的对称轴．

(2)、将拋物线的顶点A先向右平移1个单位，再向下平移1个单位后恰好与拋物线上的点B重合，求a的值．

查看试题解析
19. 已知抛物线 $y = a (x - h)^{2}$ 的对称轴为直线 $x = - 2$ ，且过点 $(1 ， - 3)$ ．

(1)、求该抛物线对应的函数表达式．

(2)、该抛物线是由抛物线 $y = a x^{2}$ 经过怎样的平移得到的？

查看试题解析
20. 已知抛物线 $y_{1} = a x^{2} - 2 a x + 1$ 与直线 $y_{2} = - x + 3$ .

(1)、求证：两个函数图象必有交点；

(2)、当抛物线 $y_{1}$ 的顶点落在直线 $y_{2}$ 上时，求a的值；

(3)、当 $- 4 < x < 2$ 时， $y_{1} < y_{2}$ ，求a的取值范围.

查看试题解析
21. 已知二次函数 $y = \frac{1}{4} {(x - 2 m)}^{2} + 3 - 4 m$ （m是实数）.

(1)、小明说：当m的值变化时，二次函数图象的顶点始终在一条直线上运动，你认为他的说法对吗？为什么？

(2)、已知点 $P (a - 5 ， t)$ ， $Q (4 m + 3 + a ， t)$ 都在该二次函数图象上，求证： $t \geq 7$ .

查看试题解析
22. 在平面直角坐标系内，二次函数 $y = x^{2} + b x + c$ 的图象经过点 $A (3 ， 0)$ 和 $B (2 ， - 3)$ ．

(1)、求这个二次函数的表达式；

(2)、求出二次函数的顶点坐标；

(3)、将该二次函数的图象向右平移几个单位，可使平移后所得的图象经过坐标原点．

查看试题解析
23. 如图，在平面直角坐标系中，一次函数 $y_{1} = k x - 7$ 的图象与二次函数 $y_{2} = 2 x^{2} + b x + c$ 的图象交于 $A (1 ， - 5)$ 、 $B (3 ， t)$ 两点.

(1)、求 $y_{1}$ 与 $y_{2}$ 的函数关系式；

(2)、直接写出当 $y_{1} < y_{2}$ 时，x的取值范围；

(3)、点C为一次函数 $y_{1}$ 图象上一点，点C的横坐标为n，若将点C向右平移2个单位，再向上平移4个单位后刚好落在二次函数 $y_{2}$ 的图象上，求n的值.

查看试题解析

2023年浙教版数学九年级上册1.2 二次函数的图象 同步测试（提高版）

一、选择题

二、填空题

三、综合题

2023年浙教版数学九年级上册1.2 二次函数的图象同步测试（提高版）