2023年浙教版数学九年级上册1.1 二次函数同步测试（提高版）

试卷更新日期：2023-08-09 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知函数 $y = (m + 3) x^{2} + 1$ 是二次函数，则m的取值范围为（）

A、 $m > - 3$ B、 $m < - 3$ C、 $m \neq - 3$ D、任意实数

查看试题解析
2. 若y＝ $(m - 1) x^{m^{2} + 1}$ 是二次函数，则m的值是（）

A、﹣1 B、1 C、1或﹣1 D、2

查看试题解析
3. 如果 $y = (m - 2) x^{2} + (m - 1) x$ 是关于x的二次函数，则m的取值范围是（）

A、 $m \neq 1$ B、 $m \neq 2$ C、 $m \neq 2$ 且 $m \neq 1$ D、全体实数

查看试题解析
4. 已知二次函数 $y = a x^{2} + x + a (a - 2)$ 的图象经过原点，则a的值为（）

A、0或2 B、0 C、2 D、无法确定

查看试题解析
5. 抛物线 $y = - a x^{2}$ ，当 $x = 2$ 时， $y = - 6$ ；当 $x = - 2$ 时， $y$ 的值是（）

A、6 B、-6 C、 $\frac{3}{2}$ D、 $- \frac{3}{2}$

查看试题解析
6. 抛物线 $y = a x^{2} + b x + c$ 经过点 $(- 1 ， 0)$ 、 $(3 ， 0)$ ，且与y轴交于点 $(0 ， - 5)$ ，则当 $x = 2$ 时，y的值为（）

A、 $- 5$ B、 $- 3$ C、 $- 1$ D、5

查看试题解析
7. 如图是一个不倒翁的部分剖面图，可看做一个抛物线，若肚子最大的宽度 $A B = 10 cm$ ， $O D = 15 cm$ ，按图示位置建立的平面直角坐标系可知，抛物线表达式为（）

A、 $y = \frac{3}{5} x^{2}$ B、 $y = - \frac{3}{5} x^{2}$ C、 $y = \frac{3}{16} x^{2}$ D、 $y = - \frac{3}{16} x^{2}$

查看试题解析
8. 如图，二次函数y=x²+bx+c的图象过点B(0，-2).它与反比例函数 $y = - \frac{8}{x} (x < 0)$ 的图象交于点A(m，4)，则这个二次函数的关系式为（）

A、 $y = x^{2} - x - 2$ B、 $y = x^{2} - x + 2$ C、 $y = x^{2} + x - 2$ D、 $y = x^{2} + x + 2$

查看试题解析
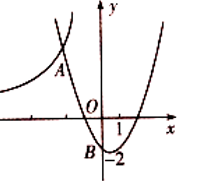9. 据省统计局公布的数据，安徽省2019年第二季度GDP总值约为7.9千亿元人民币，若我省第四季度GDP总值为y千亿元人民币，平均每个季度GDP增长的百分率为x ，则y关于x的函数表达式是（）

A、y=7.9（1＋2x） B、y=7.9（1－x）² C、y=7.9（1＋x）² D、y=7.9＋7.9（1＋x）＋7.9（1＋x）²

查看试题解析
10. 用20cm长的绳子围成一个矩形，如果这个矩形的一边长为xcm，面积是Scm² ，则S与x的函数关系式为（）

A、S＝x（20﹣x） B、S＝x（20﹣2x） C、S＝x（10﹣x） D、S＝2x（10﹣x）

查看试题解析

二、填空题（每空4分，共24分）

11. 若 $y = (m - 3) x^{m^{2} - 5 m + 8} + 2 x - 3$ 是关于x的二次函数，则m的值是．

查看试题解析
12. 有下列函数：
①y＝5x-4；②y＝ $\frac{2}{3} x^{2} - 6 x$ ；③y＝2x³-8x²+3；④y＝ $\frac{3}{8}$ x²-1；⑤y＝ $\frac{3}{x^{2}} - \frac{1}{x} - 2$ ；

其中属于二次函数的是（填序号）．

查看试题解析
13. 如图所示的抛物线是二次函数y＝（m-2）x²-3x+m²+m-6的图象，那么m的值是.

查看试题解析
14. 对于二次函数y＝x²－2mx－3，当x＝2时的函数值与x＝8时的函数值相等时，m＝．

查看试题解析
15. 如图，用长为16m的篱笆，一面利用墙（墙足够长）围成一块留有一扇1m宽的门的长方形花圃．设花圃的宽AB为xm，面积为ym² ，则y与x的函数表达式为．

查看试题解析
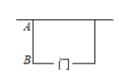16. 一台机器原价50万元，如果每年的折旧率是x，两年后这台机器的价格为y万元，则y与x的函数关系式为．

查看试题解析

三、解答题（共8题，共66分）

17. 如图，在平面直角坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A(1，0)，B(0，2)，抛物线y= $\frac{1}{2}$ x²+bx-2过点C．求抛物线的表达式．

查看试题解析
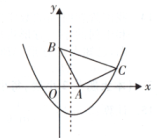18. 当m为何值时，函数 $y = (m + 1) x^{m^{2} - 2 m - 1} + 8 x - 1$ 是二次函数．

查看试题解析
19. 如图，在四边形ABCD中，∠BAD＝∠ACB＝90°，AB＝AD，AC＝4BC，设CD的长为x，四边形ABCD的面积为y，求y与x之间的函数表达式．

查看试题解析
20. 已知函数y=（|m|-1）x²+（m+1)x+3.

(1)、若这个函数是一次函数，求m的值；

(2)、若这个函数是二次函数，求m的取值范围.

查看试题解析
21.

(1)、二次函数 $y = x^{2} + b x + c$ 的图象过点 $B (0 ， - 3)$ ，它与反比例函数 $y = - \frac{6}{x}$ 的图象交于点 $A (m ， 3)$ ，试求这个二次函数的解析式．

(2)、解方程： $3 x^{2} - 4 x - 1 = 0$ ．

查看试题解析
22. 在平面直角坐标系中，抛物线y＝x²+bx+c经过点(﹣1，9)、(2，﹣3)．

(1)、求这条抛物线所对应的函数表达式；

(2)、点P是这条抛物线上一点，其横、纵坐标互为相反数，求点P的坐标．

查看试题解析
23. 已知直线 $y = - x + 4$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B .$ 第一象限的点 $P (m ， n)$ 在直线 $y = - x + 4$ 上，过点 $P$ 作 $P C ⊥ x$ 轴于点 $C$ ，过点 $P$ 作 $P D ⊥ y$ 轴于点 $D$ ，设长方形 $O C P D$ 的面积为 $S$ ．

(1)、 $A ($ ， $)$ ， $B ($ ， $)$ ；

(2)、求 $S$ 关于 $m$ 的函数解析式，写出 $m$ 的取值范围；

(3)、当 $S = 2$ 时，求点 $P$ 的坐标．

查看试题解析
24. 某商场经营某种品牌的玩具，购进时的价格是30元/件，根据市场调查：在一段时间内，当销售价格是40元/件时，销售量是600件．当销售单价每涨1元，就会少售出10件玩具．

销售价格(元/件)

x

销售量y(件)

销售玩具获得的利润w(元)

(1)、不妨设该种品牌玩具的销售价格为x元/件(x＞40)，请你分别用含x的代数式来表示销售量y件和销售该品牌玩具获得的利润w元，并把化简后的结果填写在表格中：

(2)、在第(1)问的条件下，若商场获得了10000元的销售利润，求该玩具的销售价格应定为多少元/件．

查看试题解析

销售价格(元/件)	x
销售量y(件)
销售玩具获得的利润w(元)

2023年浙教版数学九年级上册1.1 二次函数 同步测试（提高版）

一、选择题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学九年级上册1.1 二次函数同步测试（提高版）