2023年浙教版数学九年级上册1.1 二次函数同步测试（培优版）

试卷更新日期：2023-08-09 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知 $y$ 关于 $x$ 的二次函数解析式为 $y = (m - 2) x^{| m |}$ ，则 $m =$ （）

A、±2 B、1 C、-2 D、±1

查看试题解析
2. 若关于x的函数 $y = （ 2 - {a）x}^{2} - x$ 是二次函数，则a的取值范围是（）

A、a≠0 B、a≠2 C、a＜2 D、a＞2

查看试题解析
3. 下面两个问题中都有两个变量：
①矩形的周长为20，矩形的面积y与一边长x；②矩形的面积为20，矩形的宽y与矩形的长x．其中变量y与变量x之间的函数关系表述正确的是（）

A、①是反比例函数，②是二次函数 B、①是二次函数，②是反比例函数 C、①②都是二次函数 D、①②都是反比例函数

查看试题解析
4. 已知如图，在正方形 $ABCD$ 中，点 $A 、 C$ 的坐标分别是 $(- 3 ， 9) (2 ， 0)$ ，点 $D$ 在抛物线 $y = \frac{1}{3} x^{2} + kx$ 的图像上，则 $k$ 的值是（）

A、 $\frac{5}{12}$ B、 $\frac{4}{3}$ C、 $\frac{5}{6}$ D、 $\frac{7}{4}$

查看试题解析
5. 在“探索函数 $y = a x^{2} + b x + c$ 的系数a，b，c与图象的关系”活动中，老师给出了直角坐标系中的四个点： $A (0 ， 2)$ ， $B (1 ， 0)$ ， $C (3 ， 1)$ ， $D (2 ， 3)$ ，同学们探索了经过这四个点中的三个点的二次函数的图象，发现这些图象对应的函数表达式各不相同，其中a的值最大为（）

A、 $\frac{5}{2}$ B、 $\frac{3}{2}$ C、 $\frac{5}{6}$ D、 $\frac{1}{2}$

查看试题解析
6. 已知二次函数y＝ax²+bx+c（a ， b ， c为常数，a≠0），其中，自变量x与函数值y之间满足下面对应关系：

x

……

$-$ 5

$-$ 3

$-$ 1

……

y＝ax²+bx+c

……

$-$ 2.5

1.5

1.5

……

则 $\frac{b (a + b + c)}{a}$ 的值是（　　）

A、﹣10 B、﹣5 C、﹣ $\frac{5}{2}$ D、﹣ $\frac{5}{4}$

查看试题解析
7. 2019年女排世界杯于9月在日本举行，中国女排以十一连胜的骄人成绩卫冕冠军，充分展现了团队协作、顽强拼搏的女排精神．如图是某次比赛中垫球时的动作．若将垫球后排球的运动路线近似的看作抛物线，在同一竖直平面内建立如图所示的直角坐标系，已知运动员垫球时（图中点A）离球网的水平距离为5米，排球与地面的垂直距离为0.5米，排球在球网上端0.26米处（图中点B）越过球网（女子排球赛中球网上端距地面的高度为2.24米），落地时（图中点C）距球网的水平距离为2.5米，则排球运动路线的函数表达式为（）

A、y＝﹣ $\frac{14}{75} x^{2} - \frac{8}{15} x + \frac{5}{2}$ B、y＝﹣ $\frac{14}{75} x^{2} + \frac{8}{15} x + \frac{5}{2}$ C、y＝ $\frac{14}{75} x^{2} - \frac{8}{15} x + \frac{5}{2}$ D、y＝ $\frac{14}{75} x^{2} + \frac{8}{15} x + \frac{5}{2}$

查看试题解析
8. 如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（

A、y= $\frac{4}{25} x^{2}$ B、 y= $\frac{2}{25} x^{2}$ C、 y= $\frac{2}{5} x^{2}$ D、y= $\frac{4}{5} x^{2}$

查看试题解析
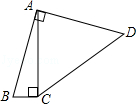9. 某农产品市场经销一种销售成本为40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨一元，月销售量就减少10千克．设销售单价为每千克x元，月销售利润为y元，则y与x的函数关系式为（　　）

A、y＝（x﹣40）（500﹣10x） B、y＝（x﹣40）（10x﹣500） C、y＝（x﹣40）[500﹣10（x﹣50）] D、y＝（x﹣40）[500﹣10（50﹣x）]

查看试题解析
10. 喜迎圣诞，某商店销售一种进价为50元/件的商品，售价为60元/件，每星期可卖出200件，若每件商品的售价每上涨1元，则每星期就会少卖出10件．设每件商品的售价上涨x元（x正整数），每星期销售该商品的利润为y元，则y与x的函数解析式为（）

A、y=﹣10x²+100x+2000 B、y=10x²+100x+2000 C、 y=﹣10x²+200x D、y=﹣10x²﹣100x+2000

查看试题解析

二、填空题（每空4分，共24分）

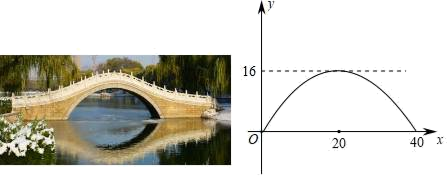
11. 若函数 $y = (m - 2) x^{m^{2} - 2 m + 2} - 6$ 是二次函数，则m的值为．

查看试题解析
12. 已知函数 $y = x^{m^{2} - m} - (m + 1) x + 4$ 是关于x的二次函数，且顶点在y轴上，那么m的值为．

查看试题解析
13. 用一根长为80cm的铁丝，把它弯成一个矩形，设矩形的面积为ycm² ，一边长为xcm，则y与x的函数表达式为（化为一般式）

查看试题解析
14. 如图①是一座石拱桥，它是一个横断面为抛物线形状的拱桥，若桥拱的最大高度为16米，跨度为40米，图②为它在坐标系中的示意图，则抛物线的解析式是（写出顶点式和一般式均可）．

查看试题解析
15. 如图，抛物线 $C_{1}$ ： $y = x^{2} + 2 x - 3$ 与抛物线 $C_{2}$ ： $y = a x^{2} + b x + c$ 组成一个开口向上的“月牙线”，抛物线 $C_{1}$ 和抛物线 $C_{2}$ 与x轴有着相同的交点A、B（点B在点A右侧），与y轴的交点分别为C、D．如果 $B D = C D$ ，那么抛物线 $C_{2}$ 的表达式是．

查看试题解析
16. 已知一个二次函数的图象经过点 $(0 ， 2)$ ，且在 $y$ 轴左侧部分是上升的，那么该二次函数的解析式可以是（只要写出一个符合要求的解析式）．

查看试题解析

三、解答题（共8题，共66分）

17. 已知 $y = (m^{2} - m) x^{m^{2} - 2 m - 1} + (m - 3) x + m^{2}$ 是x的二次函数，求出它的解析式．

查看试题解析
18. 如图，在平面直角坐标系xOy中， $△ A B C$ 是等腰直角三角形， $∠ B A C = 90 °$ ， $A (1 ， 0)$ ， $B (0 ， 2)$ ，抛物线 $y = \frac{1}{2} x^{2} + b x - 2$ 过点C．求抛物线的表达式．

查看试题解析
19. 如图，已知在平面直角坐标系中，四边形OABC是边长为3的正方形，其中点A，C分别在x轴的正半轴和y轴的正半轴上，抛物线y=-x²+bx+c经过A，C两点求b，c的值．

查看试题解析
20. 已知函数y=（m²-2）x²+（m+ $\sqrt{2}$ ）x+8．

(1)、若这个函数是一次函数，求m的值；

(2)、若这个函数是二次函数，求m的取值范围.

查看试题解析
21. 如图，已知直线l：y₁＝kx+b经过A（2，0）和B（0，2）两点，它与抛物线y₂＝ax²在第一象限内相交于点P，且△AOP的面积为1.

(1)、求点P的坐标．

(2)、求a的值，并写出抛物线的解析式．

查看试题解析
22. 定义：如图，若两条抛物线顶点相同，开口方向相反，我们就称这两条抛物线是“蝴蝶抛物线”.

(1)、已知 $y_{1} = \frac{1}{2} x^{2} - 2 x + 8$ ，若 $y_{2}$ 和 $y_{1}$ 是“蝴蝶抛物线”，且 $y_{2}$ 经过点（-1，0），求 $y_{2}$ 的解析式.

(2)、根据（1）中的结论，已知抛物线 $y_{3} = a x^{2} + b x + \frac{10}{3}$ ，且 $y_{1} + y_{3}$ 和 $y_{2}$ 是“蝴蝶抛物线”，求 $y_{3}$ 的解析式.

查看试题解析

x	……	$-$ 5	$-$ 3	$-$ 1	……
y＝ax²+bx+c	……	$-$ 2.5	1.5	1.5	……

2023年浙教版数学九年级上册1.1 二次函数 同步测试（培优版）

一、选择题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学九年级上册1.1 二次函数同步测试（培优版）