2023年浙教版数学九年级上册1.1二次函数 同步测试(基础版)
试卷更新日期:2023-08-09 类型:同步测试
一、选择题(每题3分,共30分)
-
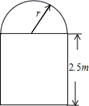
1. 下列各式中,y是x的二次函数的是( )A、 B、 C、 D、2. 二次函数的二次项系数、一次项系数和常数项分别是( )A、1, , -1 B、1,6,1 C、0,-6,1 D、0,6,-13. 若函数是二次函数,则有( )A、 B、 C、 D、4. 如图,若抛物线经过原点,则抛物线的解析式为( )
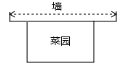
 A、 B、 C、 D、或5. 已知抛物线的顶点坐标是 , 且与y轴交于点 , 这个抛物线的解析式是( )A、 B、 C、 D、6. 已知二次函数 图象经过原点,则a的取值为( ).A、 B、 C、 D、7. 若抛物线经过 三点,则此抛物线的表达式为( )A、 B、 C、 D、8. 某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )A、y=(200﹣5x)(40﹣20+x) B、y=(200+5x)(40﹣20﹣x) C、y=200(40﹣20﹣x) D、y=200﹣5x9. 如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为ym2 , 则y关于x的函数表达式为( )
A、 B、 C、 D、或5. 已知抛物线的顶点坐标是 , 且与y轴交于点 , 这个抛物线的解析式是( )A、 B、 C、 D、6. 已知二次函数 图象经过原点,则a的取值为( ).A、 B、 C、 D、7. 若抛物线经过 三点,则此抛物线的表达式为( )A、 B、 C、 D、8. 某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )A、y=(200﹣5x)(40﹣20+x) B、y=(200+5x)(40﹣20﹣x) C、y=200(40﹣20﹣x) D、y=200﹣5x9. 如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为ym2 , 则y关于x的函数表达式为( ) A、y=- x2+26x(2≤x<52) B、y=- x2+50x(2≤x<52) C、y=-x2+52x(2≤x<52) D、y=- x2+27x-52(2≤x<52)10. 在某种病毒的传播过程中,每轮传染平均1人会传染x个人,若最初2个人感染该病毒,经过两轮传染,共有y人感染.则y与x的函数关系式为( )A、 B、 C、 D、
A、y=- x2+26x(2≤x<52) B、y=- x2+50x(2≤x<52) C、y=-x2+52x(2≤x<52) D、y=- x2+27x-52(2≤x<52)10. 在某种病毒的传播过程中,每轮传染平均1人会传染x个人,若最初2个人感染该病毒,经过两轮传染,共有y人感染.则y与x的函数关系式为( )A、 B、 C、 D、二、填空题(每空4分,共24分)
-
11. 函数是二次函数,则.12. 有下列函数:
①y=5x-4;②;③;④;⑤;
其中属于二次函数的是 (填序号).
13. 若某二次函数图象的形状和开口方向与抛物线相同,且顶点坐标为 , 则它的表达式为 .14. 小聪在画一个二次函数的图象时,列出了下面几组y与x的对应值:x
…
0
1
2
3
4
5
…
y
…
5
0
-3
-4
-3
0
…
该二次函数的解析式是 .
15. 一个矩形的周长为16cm,设一边长为xcm,面积为y ,那么y与x的关系式是16. 用一根长为80cm的铁丝,把它弯成一个矩形,设矩形的面积为ycm2 , 一边长为xcm,则y与x的函数表达式为(化为一般式)三、解答题(共8题,共66分)
-
17. 已知两个变量x,y之间的关系式为y=(a﹣2)x2+(b+2)x﹣3.(1)、当时,x,y之间是二次函数关系;
(2)、当时,x,y之间是一次函数关系.
18. 若函数y=(a-1)x(b+1)+x2+1是二次函数,试讨论a、b的取值范围。
19. 抛物线的顶点坐标为且经过点 , 求该抛物线解析式.20. 已知抛物线过点和 , 求该抛物线的解析式.21. 一个二次函数y=(k﹣1)x+2x﹣1.(1)、求k值.(2)、求当x=0.5时y的值?