广东省茂名市高州市十校2022-2023学年八年级下学期第11周学情练习数学试卷
试卷更新日期:2023-08-07 类型:月考试卷
一、单项选择题(本大题10小题,每小题3分,共30分)
-
1. 下列从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 不等式在数轴上表示正确的是( )A、
3. 不等式在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 小林是一位密码编译爱好者,在他的密码手册中有这样一条信息:3,分别对应六个字:国,爱,我,数,学,祖,现将因式分解,结果呈现的密码信息可能是( )A、我爱数学 B、爱祖国 C、祖国数学 D、我爱祖国5. 已知点在第二象限,则的取值范围是( )A、 B、 C、 D、6. 如果多项式可分解为 , 则的值分别为( )A、 B、 C、 D、7. 如图,在Rt中,是的平分线,若 , 则:为( )
4. 小林是一位密码编译爱好者,在他的密码手册中有这样一条信息:3,分别对应六个字:国,爱,我,数,学,祖,现将因式分解,结果呈现的密码信息可能是( )A、我爱数学 B、爱祖国 C、祖国数学 D、我爱祖国5. 已知点在第二象限,则的取值范围是( )A、 B、 C、 D、6. 如果多项式可分解为 , 则的值分别为( )A、 B、 C、 D、7. 如图,在Rt中,是的平分线,若 , 则:为( ) A、5:13 B、12:13 C、12:5 D、13:58. 如图,绕点逆时针旋转得到 , 若 , 则的度数是( )
A、5:13 B、12:13 C、12:5 D、13:58. 如图,绕点逆时针旋转得到 , 若 , 则的度数是( ) A、 B、 C、 D、9. 如图,函数和的图象相交于点 , 则关于x的不等式的解集是( )
A、 B、 C、 D、9. 如图,函数和的图象相交于点 , 则关于x的不等式的解集是( ) A、 B、 C、 D、10. 四边形ABCD中, , 则等于( )
A、 B、 C、 D、10. 四边形ABCD中, , 则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题5小题,每小题3分,共15分)
-
11. 用不等式表示:“x的2倍与1的差小于3”是.12. 分解因式: .13. 如图,把沿方向平移得到 , 则的长是.
 14. 如图,在中, , , , D为的中点,P为上一动点,连接 , , 则的最小值是.
14. 如图,在中, , , , D为的中点,P为上一动点,连接 , , 则的最小值是.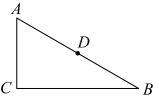 15. 若关于的不等式组有解,则的取值范围是.
15. 若关于的不等式组有解,则的取值范围是.三、解答题(一)(本大题共3小题,每小题8分,共24分)
-
16. 解不等式 , 并在数轴上表示解集.17. 因式分解:18. 解不等式组 , 并求出它的整数解.
四、解答题(二)(本大共题3小题,每小题9分,共27分)
-
19. 如图,在平面直角坐标系中,的三个顶点分别是 , 将先向左平移6个单位长度,再向上平移5个单位长度,得到对应的.
 (1)、画出平移后的;(2)、若BC边上一点经过上述平移后的对应点为 , 请直接写出点的坐标(用含的式子表示);(3)、连接 , 求的面积.20. 一种混凝土排水管,其形状为空心的圆柱体,它的内径 , 外径 , 长.浇制一节这样的排水管需要多少立方米的混凝土?(用简便方法计算,结果保留).
(1)、画出平移后的;(2)、若BC边上一点经过上述平移后的对应点为 , 请直接写出点的坐标(用含的式子表示);(3)、连接 , 求的面积.20. 一种混凝土排水管,其形状为空心的圆柱体,它的内径 , 外径 , 长.浇制一节这样的排水管需要多少立方米的混凝土?(用简便方法计算,结果保留). 21. 如图,点B、F、C、E在同一直线上,AC、DF相交于点 , 垂足为 , 垂足为 , 且.
21. 如图,点B、F、C、E在同一直线上,AC、DF相交于点 , 垂足为 , 垂足为 , 且.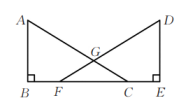 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数.五、解管题(三)(本大题共2小题,每小题12分,共24分)
-
22. 某学校购买一批篮球和排球,已知购买2个篮球和1个排球需170元,购买5个篮球和2个排球需400元.(1)、分别求篮球和排球的单价.(2)、该学校准备购买篮球和排球共100个,每种球至少买一个且篮球个数不少于排球个数的3倍.
①设购买篮球(个),总费用为(元),写出关于的函数表达式并写出自变量的取值范围;
②请设计总费用最低的购买方案,并求出最低费用.
23. 如图1,中, , 将绕点逆时针旋转得到与AB交于点 , CD分别交OB、AB于点E、F. (1)、求证:∠A=∠D;(2)、求证:(3)、如图2,当旋转到∠AOD=180°时,此时恰好 , 求CD长.
(1)、求证:∠A=∠D;(2)、求证:(3)、如图2,当旋转到∠AOD=180°时,此时恰好 , 求CD长.