浙江省嘉兴市2022-2023学年七年级下学期数学期末试卷
试卷更新日期:2023-08-07 类型:期末考试
一、选择题(每小题有4个选项,其中有且只有一个正确,请把正确选项的代码填入答题卷的相应空格,每小题3分,共30分)
-
1. 计算: , 结果正确的是( )A、 B、 C、 D、2. 观察下列五幅图案,在②、③、④、⑤的图案中可以通过平移图案①得到的是( )
 A、② B、③ C、④ D、⑤3. 红细胞是血液中最多的一类血细胞,它的平均直径是0.0000072米,数据0.0000072用科学记数法表示为( )A、 B、 C、 D、4. 如图,直线a,b被直线c所截,∠1的内错角是( )
A、② B、③ C、④ D、⑤3. 红细胞是血液中最多的一类血细胞,它的平均直径是0.0000072米,数据0.0000072用科学记数法表示为( )A、 B、 C、 D、4. 如图,直线a,b被直线c所截,∠1的内错角是( )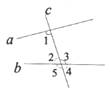 A、∠2 B、∠3 C、∠4 D、∠55. 下列由左边到右边的变形中,属于因式分解的是( )A、 B、 C、 D、6. 某校学生喜爱的体育中考项目人数的扇形统计图如图,已知喜爱排球的人数为440人,则喜爱游泳的人数为( )
A、∠2 B、∠3 C、∠4 D、∠55. 下列由左边到右边的变形中,属于因式分解的是( )A、 B、 C、 D、6. 某校学生喜爱的体育中考项目人数的扇形统计图如图,已知喜爱排球的人数为440人,则喜爱游泳的人数为( ) A、56人 B、120人 C、184人 D、800人7. 方程是关于x,y的二元一次方程,则的值为( )A、0 B、2 C、0或2 D、38. 某工程队需要铺设一条长为2400米的公路,铺设时“...”,设原计划每天铺设米,可得方程 , 根据此情景,题中用“...”表示的缺失条件应补为( )A、实际每天铺设比原计划多铺设20米,结果提前6天完成 B、实际每天铺设比原计划少铺设20米,结果提前6天完成 C、实际每天铺设比原计划多铺设20米,结果延期6天完成 D、实际每天铺设比原计划少铺设20米,结果延期6天完成9. 若关于x,y的方程组的解为 , 则的值为( )A、-3 B、 C、 D、110. 已知矩形ABCD,将两张边长分别为和的正方形纸片按图1,图2两种方式放置(图1,图2两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1与图2中阴影部分的周长差为 , 若要知道的值,只需测量( )
A、56人 B、120人 C、184人 D、800人7. 方程是关于x,y的二元一次方程,则的值为( )A、0 B、2 C、0或2 D、38. 某工程队需要铺设一条长为2400米的公路,铺设时“...”,设原计划每天铺设米,可得方程 , 根据此情景,题中用“...”表示的缺失条件应补为( )A、实际每天铺设比原计划多铺设20米,结果提前6天完成 B、实际每天铺设比原计划少铺设20米,结果提前6天完成 C、实际每天铺设比原计划多铺设20米,结果延期6天完成 D、实际每天铺设比原计划少铺设20米,结果延期6天完成9. 若关于x,y的方程组的解为 , 则的值为( )A、-3 B、 C、 D、110. 已知矩形ABCD,将两张边长分别为和的正方形纸片按图1,图2两种方式放置(图1,图2两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1与图2中阴影部分的周长差为 , 若要知道的值,只需测量( )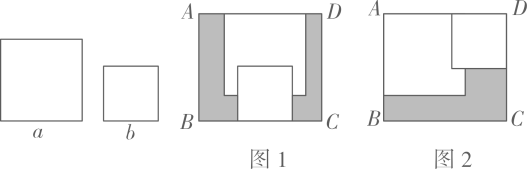 A、 B、 C、BC D、AB
A、 B、 C、BC D、AB二、填空题(本题有6小题,每小题3分,共18分)
-
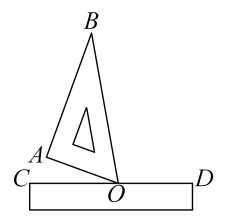
11. 若分式 有意义,则x的取值范围是 .12. 已知某组数据的频率为0.4,样本容量为820,则这组数据的频数为.13. 计算: =.14. 如图,将直角三角板ABO的顶点放于直尺边CD上, , 要使 , 至少将直角三角板绕点顺时针旋转°.
 15. 若 , 则.16. 现有A,B两袋糖果,其中袋中水果糖的重量占 , 其余都为奶糖,袋中奶糖的重量占 , 其余都为水果糖.将两袋糖果混合在一起,发现水果糖的重量占总重量的.(1)、当时,原来袋的重量占混合后糖果总重量的百分比为.(2)、当时,原来袋的重量占混合后糖果总重量的百分比为.
15. 若 , 则.16. 现有A,B两袋糖果,其中袋中水果糖的重量占 , 其余都为奶糖,袋中奶糖的重量占 , 其余都为水果糖.将两袋糖果混合在一起,发现水果糖的重量占总重量的.(1)、当时,原来袋的重量占混合后糖果总重量的百分比为.(2)、当时,原来袋的重量占混合后糖果总重量的百分比为.三、解答题(本题有8小题,第 rId121 题每题6分,第23、24题每题8分,共52分
-
17. 计算:(1)、.(2)、.18. 分解因式:(1)、(2)、19. 先化简,再求值: , 其中.20. 已知关于x,y的二元一次方程组其中是实数.(1)、当时,求该二元一次方程组的解.(2)、若是的2倍,求的值.21. 为了解某中学学生对“生命安全知识”知晓情况,现从中随机抽取部分学生进行问卷调查.其结果根据分数段划分为五个等级,结果绘制如下统计图表:
分数段
等级
频数
频率
x<60
不清楚
9
0.03
60≤x<70
不太清楚
n
0.07
70≤x<80
基本清楚
75
m
80≤x<90
比较清楚
135
90≤x≤100
非常清楚
60
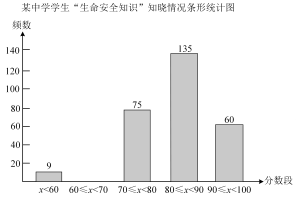 (1)、参与本次调查的学生有多少人?(2)、求表中m,n的数值,并补全频数分布直方图.(3)、若该校有1200名学生,请估计这些学生中“比较清楚”生命安全知识的人数.22. 已知:如图,.
(1)、参与本次调查的学生有多少人?(2)、求表中m,n的数值,并补全频数分布直方图.(3)、若该校有1200名学生,请估计这些学生中“比较清楚”生命安全知识的人数.22. 已知:如图,.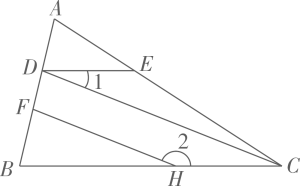 (1)、判断FH与CD的位置关系,并说明理由.(2)、若求∠2的度数.23. 关于任意实数存在一种新运算有如下结果:
(1)、判断FH与CD的位置关系,并说明理由.(2)、若求∠2的度数.23. 关于任意实数存在一种新运算有如下结果:;
按你发现的规律探索:
(1)、.(用的代数式表示).(2)、当成立时,求满足的关系式.24. 甲、乙两小区准备安装A、B两款智能快递柜,每个款能满足快递需求人数比款多20人.已知甲、乙两小区有快递需求居民分别有280人、420人.如果甲小区全部安装款智能快递柜,乙小区全部安装款智能快递柜,那么刚好满足两小区所有居民的快递需求且安装个数相同. (1)、设每个款能满足快递需求人数为人,求的值.(2)、如果甲小区安装款和款智能快递柜共7个,其中安装款的个数比安装款的2倍还多1个,分别求甲小区款和款的安装个数,并说明这样安装能否满足甲小区所有居民的快递需求.(3)、已知购买款需6000元/个,购买款需6800元/个,请你帮助乙小区设计一个购买方案,既刚好满足乙小区所有居民的快递需求,又费用最省,并说明理由.
(1)、设每个款能满足快递需求人数为人,求的值.(2)、如果甲小区安装款和款智能快递柜共7个,其中安装款的个数比安装款的2倍还多1个,分别求甲小区款和款的安装个数,并说明这样安装能否满足甲小区所有居民的快递需求.(3)、已知购买款需6000元/个,购买款需6800元/个,请你帮助乙小区设计一个购买方案,既刚好满足乙小区所有居民的快递需求,又费用最省,并说明理由.