广东省韶关市2022-2023学年八年级下学期数学期末试卷
试卷更新日期:2023-08-07 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 下列各式中,正确的是( )A、 B、 C、 D、2. 一次函数的图象不经过的象限是 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知中,a、b、c分别是的对边,下列条件不能判断是直角三角形的是( )A、 B、 C、 D、4. 计算的结果是( )A、 B、 C、-1 D、15. 如图,在平行四边形ABCD中,BF平分 , 交AD于点F,CE平分 , 交AD于点 , 则BC长为( )
 A、11 B、14 C、9 D、106. 把一张长方形纸片ABCD按如图方式折叠,使顶点和点重合,折痕为EF.若 , , 则DF的长为( )
A、11 B、14 C、9 D、106. 把一张长方形纸片ABCD按如图方式折叠,使顶点和点重合,折痕为EF.若 , , 则DF的长为( ) A、3 B、4 C、4.8 D、57. 下列命题中,是真命题的有( )
A、3 B、4 C、4.8 D、57. 下列命题中,是真命题的有( )①对角线相等且互相平分的四边形是矩形
②对角线互相垂直的四边形是菱形
③对角线互相平分的四边形是平行四边形
④对角线相等的菱形是正方形
A、①②③ B、①③④ C、②③④ D、①②④8. 已知正比例函数y=kx,且y随x的增大而减少,则直线y=2x+k的图象是( )A、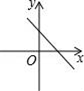 B、
B、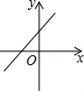 C、
C、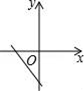 D、
D、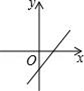 9. 如图,平行四边形ABCD的对角线相交于点 , 且 , 过作交BC于点 , 若的周长为10,则的值是( )
9. 如图,平行四边形ABCD的对角线相交于点 , 且 , 过作交BC于点 , 若的周长为10,则的值是( ) A、10 B、15 C、20 D、2510. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为.若 , 则的值是( )
A、10 B、15 C、20 D、2510. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为.若 , 则的值是( ) A、30 B、20 C、18 D、10
A、30 B、20 C、18 D、10二、填空题(本大题共5小题,每小题3分,共15分)
-
11. 已知实数m、n满足 , 则 .12. 如果数据的平均数是5,那么的平均数是.13. 如图,以Rt的三边为直径分别向外作半圆,若斜边 , 则图中阴影部分的面积为.
 14. 已知一次函数与的图象在轴上相交于同一点,则.15. 如图,是内一点,分别是AB,AC,CD,BD的中点,则四边形EFGH的周长为.
14. 已知一次函数与的图象在轴上相交于同一点,则.15. 如图,是内一点,分别是AB,AC,CD,BD的中点,则四边形EFGH的周长为.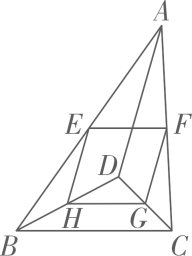
三、解答题(一)(本大题共3小题,每小题8分,共24分)
-
16. 计算: .17. 如图,正方形网格的每个小方格边长均为的顶点在格点上.
 (1)、判断的形状,并说明理由;(2)、直接写出AC边上的高的长度=.18. 如图,在平面直角坐标系中,直线l1:y=ax+4与x轴,y轴分别交于点B,A,且与直线l2:y=kx相交于点C(2,2).
(1)、判断的形状,并说明理由;(2)、直接写出AC边上的高的长度=.18. 如图,在平面直角坐标系中,直线l1:y=ax+4与x轴,y轴分别交于点B,A,且与直线l2:y=kx相交于点C(2,2).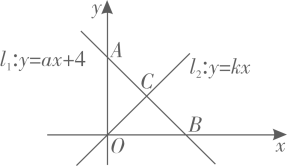 (1)、求和的值;(2)、直线与轴围成的三角形面积为;(3)、的解集为.
(1)、求和的值;(2)、直线与轴围成的三角形面积为;(3)、的解集为.四、解答题(二)(本大题共3小题,每小题9分,共27分)
-
19. 如图:在菱形ABCD中,对角线AC、BD交于点 , 过点作于点 , 延长BC至点 , 使 , 连接DF.
 (1)、求证:四边形AEFD是矩形;(2)、若BF=16,DF=8,连接OF,求OF的长.20. 某中学随机从七、八年级中各抽取20名选手组成代表队参加党史知识竞赛,计分采用10分制,选手得分均为整数,这次竞赛后,将七、八年级两支代表队选手成绩,对应整理绘制如下两幅不完整的统计图:
(1)、求证:四边形AEFD是矩形;(2)、若BF=16,DF=8,连接OF,求OF的长.20. 某中学随机从七、八年级中各抽取20名选手组成代表队参加党史知识竞赛,计分采用10分制,选手得分均为整数,这次竞赛后,将七、八年级两支代表队选手成绩,对应整理绘制如下两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)、请根据以上信息补全条形统计图;(2)、七年级代表队学生成绩的平均数是 , 中位数是 , 众数是;(3)、八年级代表队学生成绩扇形统计图中,的值是;8分成绩对应的圆心角度数是度;(4)、该校八年级有500人,根据抽样调查的结果,请你估计该校八年级学生中有多少名学生的成绩是9分?21. 如图,在中,是BC边上的一点,是AD的中点,过点作BC的平行线交CE的延长线于点 , 且 , 连接BF. (1)、线段BD与CD有什么数量关系?并说明理由;(2)、当满足什么条件时,四边形AFBD是菱形?并说明理由.
(1)、线段BD与CD有什么数量关系?并说明理由;(2)、当满足什么条件时,四边形AFBD是菱形?并说明理由.五、解答题(三)(本大题共2小题,每小题12分,共24分)
-
22. 某学校要购买甲、乙两种消毒液,用于预防新型冠状病毒.若购买9桶甲消毒液和6桶乙消毒液,则一共需要615元;若购买8桶甲消毒液和12桶乙消毒液,则一共需要780元.(1)、每桶甲消毒液、每桶乙消毒液的价格分别是多少元?(2)、若该校计划购买甲、乙两种消毒液共30桶,其中购买甲消毒液α桶,且甲消毒液的数量至少比乙消毒液的数量多5桶,又不超过乙消毒液的数量的2倍.怎样购买才能使总费用W最少?并求出最少总费用.23. 如图,平面直角坐标系中,直线与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
 (1)、求点C的坐标及直线AB的表达式;(2)、如图,在x轴上有一点E,过点E作直线轴,交直线y=2x于点F,交直线于点G,若GF的长为3.求点E的坐标;(3)、在轴上是否存在一点 , 使以为顶点的三角形是等腰三角形,若存在,直接写出点的坐标;若不存在,说明理由.
(1)、求点C的坐标及直线AB的表达式;(2)、如图,在x轴上有一点E,过点E作直线轴,交直线y=2x于点F,交直线于点G,若GF的长为3.求点E的坐标;(3)、在轴上是否存在一点 , 使以为顶点的三角形是等腰三角形,若存在,直接写出点的坐标;若不存在,说明理由.