广东省汕头市潮阳区2022-2023学年八年级下学期期末考试数学试题

试卷更新日期：2023-08-07 类型：期末考试

进入 出卷网 下载

一、选择题(本大题10小题，每小题3分，共30分)

  • 1. 已知等腰三角形有两条边的长分别是3，7，则这个等腰三角形的周长为（ ）
    A、17 B、13 C、17或13 D、10

    查看试题解析

  • 2. 下列各组数中，不能构成直角三角形的是（ ）
    A、3、4、5 B、6、8、10 C、8、15、17 D、10、12、15

    查看试题解析

  • 3. 下列二次根式中，是最简二次根式的为（ ）
    A、a B、7 C、0.5 D、18

    查看试题解析

  • 4. 若式子2−a在实数范围内有意义，则a的取值范围是（ ）
    A、a≤2 B、a≥2 C、a>2 D、a<2

    查看试题解析

  • 5. 下列函数中，表示y是x的正比例函数的是（ ）
    A、y＝－2x＋1 B、y＝2x2 C、y2＝2x D、y＝2x

    查看试题解析

  • 6. 把y＝2x＋1的图象沿y轴向下平移5个单位长度后所得图象的解析式是（ ）
    A、y＝2x＋5 B、y＝2x＋6 C、y＝2x－4 D、y＝2x＋4

    查看试题解析

  • 7. 若13的整数部分为a，小数部分为b，则(a＋13)b的值是（ ）
    A、－4 B、4 C、13－3 D、13+ 4

    查看试题解析

  • 8. 如图，在▱ABCD中，由尺规作图的痕迹，判断下列结论中不一定成立的是（ ）

    A、∠DAE=∠BAE B、AD=DE C、DE=BE D、BC=DE

    查看试题解析

  • 9. 父亲节，学校《文苑》专栏登载了某同学回忆父亲的小诗：“同辞家门赴车站，别时叮咛语千万。学子满载信心去，老父怀抱希望还。”如果用纵轴表示父亲和学子在行进中离家的距离，横轴表示离家的时间，那么下列图象中，与上述诗意大致吻合的是 （ ）
    A、 B、 C、 D、

    查看试题解析

  • 10.  一次函数y＝ax＋b与y＝cx＋d的图象如图所示，下列说法：

    ① 对于函数y＝－ax＋b来说，y随x的增大而增大； ②函数y＝ax＋d不经过第四象限；③不等式ax－d≥cx－b的解集是x≥4；④ 4(a－c)＝d－b。其中正确的有（ ）

    A、4个 B、3个 C、2个 D、1个

    查看试题解析

二、填空题(本大题5小题，每小题3分，共15分)

  • 11. 若m2﹣n2=6，且m﹣n=2，则m+n= ．

    查看试题解析

  • 12. 若点（m，n）在函数y=2x+1的图象上，则2m﹣n的值是 ．

    查看试题解析

  • 13. 在平面直角坐标系中，点P(2，-3)到原点的距离是.

    查看试题解析

  • 14.  某校五个小组在一次植树活动中植树株数的统计图如图所示，则平均每组植树株. 

    查看试题解析

  • 15.  菱形ABCD，点A，B，C，D均在坐标轴上. ∠ABC＝120°，点A(－6，0)，点E是CD的中点，点P是OC上的一动点，则△PDE周长的最小值是 . 

    查看试题解析

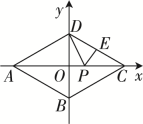
三、解答题(一)(本大题3小题，每小题8分，共24分)

  • 16. 计算：48÷3+12×12−24.

    查看试题解析

  • 17.  如图，在平行四边形ABCD中，过点D作DE⊥AB于点，点F在边CD上，且FC=AE，连接AF、BF. 求证：四边形DEBF是矩形。

    查看试题解析

  • 18.  如图，某公园有一块四边形空地ABCD，公园管理处计划在四边形ABCD区域内种植草坪，绿化环境，并在AC处修一条小路. 经测量，∠B＝90°，AB＝10米，BC＝20米，CD＝20米，AD＝30米。

    (1)、求小路AC的长；
    (2)、求种植草坪的面积。

    查看试题解析

四、解答题(二)(本大题3小题，每小题9分，共27分)

  • 19.  为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图部分如图所示。

    大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表。

    一周诗词诵背数量

    3首

    4首

    5首

    6首

    7首

    8首

    人数

    10

    10

    15

    40

    25

    20

    请根据调查的信息分析：

    (1)、活动启动之初学生“一周诗词诵背数量”的中位数为；
    (2)、估计大赛后一个月该校学生一周诗词诵背6首(含6首以上)的人数；
    (3)、选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果。

    查看试题解析

  • 20.  为宣传“人海和谐共生”的环保理念，某海洋馆面向社会推出优惠活动，活动套餐如下：

    套餐一：购买会员卡，购买门票打五折；

    套餐二：不购买会员卡，购买门票打七五折。

    若在此优惠活动期间购买一张会员卡的费用为40元，游玩x次，按套餐一所需费用为y1元，且y1＝k1x＋b(k1≠0)；按套餐二所需费用为y2元，且y2＝k2x(k2≠0)，其函数图象如图。

    (1)、求k1和b的值；
    (2)、小明在优惠活动期间来此海洋馆游玩8次，选择哪种方案合算？请说明理由。

    查看试题解析

  • 21. 用四个全等的直角三角形拼成如图①所示的大正方形，中间也是一个正方形，它是美丽的弦图，其中四个直角三角形的直角边长分别为a，b(a＜b)，斜边长为c.

    (1)、结合图①，求证：a2＋b2＝c2. 
    (2)、如图②，将这四个全等的直角三角形无缝隙无重叠地拼接在一起，得到图形ABCDEFGH. 若该图形的周长为24，OB＝3. 求该图形的面积。

    查看试题解析

五、解答题(三)(本大题2小题，每小题12分，共24分)

  • 22. 如图，在平面直角坐标系中，直线y=-x+3分别与x轴，y轴交于点A，B，点P(1，m)在直线y=-x+3上。

    (1)、求点A，B的坐标；
    (2)、若C是x轴的负半轴上一点，且S△PAC=79S△AOB ， 求直线PC的表达式；
    (3)、在（2）的条件下，若E是直线AB上一动点，过点E作EQ//x轴交直线PC于点Q，EM⊥x轴于点M，是否存在点E，使得三角形EMQ为等腰直角三角形？若存在，请直接写出点E的坐标；若不存在，请说明理由。

    查看试题解析

  • 23.  已知正方形ABCD，以CE为边在正方形ABCD外部作正方形CEFG，连接AF，点H是AF的中点，连接BH，HE

    (1)、如图所示，点E在边CB上时，则BH，HE的关系为；
    (2)、如图所示，点在BC延长线上，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请给出新的结论并证明。
    (3)、如图，点B、E、F在同一条直线上，求证：BH⊥EH.

    查看试题解析