广东省东莞市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-07 类型:期末考试
一、单选题
-
1. 等于( )A、 B、 C、2 D、42. 在直角三角形中,两条直角边长分别为6和8,则斜边的长为( )A、6 B、8 C、10 D、123. 甲、乙、丙三人进行立定跳远测试,他们的平均成绩相同,方差分别是: , , , 其中成绩最稳定的是( )A、甲 B、乙 C、丙 D、三个都一样4. 如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点M、N,测量得米,则A,B两点间的距离为( )
 A、30米 B、32米 C、36米 D、48米5. 点在一次函数的图象上,则b的值为( )A、2 B、3 C、4 D、56. 以下列各组数为边长,可以构成直角三角形的是( )A、 B、 C、 D、7. 下列计算中,正确的是( )A、 B、 C、 D、÷=58. 一次函数的函数值y随x的增大而增大,则k的值可能是( )A、 B、 C、 D、19. 如图,的对角线与相交于点O,添加下列条件不能证明是菱形的是( )
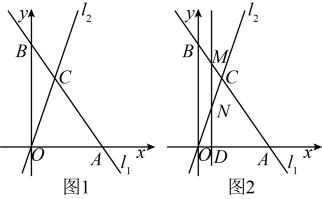
A、30米 B、32米 C、36米 D、48米5. 点在一次函数的图象上,则b的值为( )A、2 B、3 C、4 D、56. 以下列各组数为边长,可以构成直角三角形的是( )A、 B、 C、 D、7. 下列计算中,正确的是( )A、 B、 C、 D、÷=58. 一次函数的函数值y随x的增大而增大,则k的值可能是( )A、 B、 C、 D、19. 如图,的对角线与相交于点O,添加下列条件不能证明是菱形的是( ) A、 B、 C、 D、10. 如图,已知点 , 当直线与线段有交点时,k的取值范围是( )
A、 B、 C、 D、10. 如图,已知点 , 当直线与线段有交点时,k的取值范围是( ) A、 B、或 C、 D、
A、 B、或 C、 D、二、填空题
-
11. 若二次根式 有意义,则x的取值范围是
12. 数据1,3,4,3,5的众数是 .13. 点 , 在一次函数的图象上,则(填“”“”或“”)14. 如图,等边三角形的边长是 , 则高的长是 . 15. 如图,矩形对角线相交于点O,E为上一点,连接 , F为的中点,连接 , 若 , 则的长为 .
15. 如图,矩形对角线相交于点O,E为上一点,连接 , F为的中点,连接 , 若 , 则的长为 .
三、解答题
-
16. 计算: .17. 如图,已知一次函数 , 完成下列问题:
 (1)、图象与x轴的交点坐标是 , 与y轴的交点坐标是;(2)、在所给直角坐标系中画出此函数的图象;(3)、根据图象回答:当x时, .18. 如图,在中,对角线与相交于点O,点E、F分别在和的延长线上,且 , 连接 . 求证:四边形是平行四边形.
(1)、图象与x轴的交点坐标是 , 与y轴的交点坐标是;(2)、在所给直角坐标系中画出此函数的图象;(3)、根据图象回答:当x时, .18. 如图,在中,对角线与相交于点O,点E、F分别在和的延长线上,且 , 连接 . 求证:四边形是平行四边形. 19. 某地区在一次八年级数学检测中,有一道满分8分的解答题,按评分标准,所有学生的得分只有四种:0分、3分、5分、8分,老师为了了解学生的得分情况,从全区5000名考生的试卷中随机抽取一部分,通过分析与整理,绘制出如下两幅不完整的统计图.请根据相关信息,解答下列问题:
19. 某地区在一次八年级数学检测中,有一道满分8分的解答题,按评分标准,所有学生的得分只有四种:0分、3分、5分、8分,老师为了了解学生的得分情况,从全区5000名考生的试卷中随机抽取一部分,通过分析与整理,绘制出如下两幅不完整的统计图.请根据相关信息,解答下列问题: (1)、图2中a的值为 , b的值为;(2)、此样本数据的平均数是 , 中位数是;(3)、请估计该地区此题得满分(即8分)的学生人数.20. 在矩形中,点在上, , 且 , 垂足为 .
(1)、图2中a的值为 , b的值为;(2)、此样本数据的平均数是 , 中位数是;(3)、请估计该地区此题得满分(即8分)的学生人数.20. 在矩形中,点在上, , 且 , 垂足为 . (1)、求证:;(2)、若 , , 求的长.21. 观察下列等式,解答后面的问题:
(1)、求证:;(2)、若 , , 求的长.21. 观察下列等式,解答后面的问题:①;
②;
③;
……
(1)、请直接写出第⑤个等式是(不用化简);(2)、根据上述规律猜想:若n为正整数,请用含n的式子表示第n个等式,并给予证明.