广东省佛山市禅城区2022-2023学年七年级下学期数学期末试题

试卷更新日期：2023-08-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在“双碳”目标背景下，中国未来发展离不开新能源产业发展．下列能源产业图标中，不是轴对称图形的是（）

A、水能 B、核聚变能 C、太阳能 D、矿物能

查看试题解析
2. 根据测试，华为首款5G手机传输1M的文件只需0.0025秒，其中0.0025用科学记数法表示为（）

A、2.5×10^－3 B、2.5×10^－4 C、25×10^－4 D、0.25×10^－2

查看试题解析
3. 如图，直线a ， b被直线c所截，下列说法正确的是（）

A、 $∠ 1$ 与 $∠ 2$ 是内错角 B、 $∠ 3$ 与 $∠ 4$ 是对顶角 C、 $∠ 2$ 与 $∠ 3$ 是同旁内角 D、 $∠ 1$ 与 $∠ 4$ 是同位角

查看试题解析
4. 下列长度的三条线段能构成三角形的是（）

A、 $4$ ， $6$ ， $10$ B、 $2$ ， $5$ ， $8$ C、 $3$ ， $4$ ， $5$ D、 $5$ ， $7$ ， $13$

查看试题解析
5. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{5}$ B、 ${(3 a)}^{2} = 6 a^{2}$ C、 $a^{3} + a^{3} = a^{6}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
6. 以下事件属于必然事件的是（）

A、同一年出生的370人中至少有两人的生日相同 B、早上的太阳从西方升起 C、两边及一角分别相等的两个三角形全等 D、任意掷一枚质地均匀的骰子，掷出的点数是偶数

查看试题解析
7. 五线谱是一种记谱法，通过五根等距离的平行线上标以不同的音符构成旋律，如图， $A B$ 和 $C D$ 是五线谱上的两条线段，点E在 $A B$ ， $C D$ 之间的一条平行线上，若 $∠ 1 = 120 °$ ， $∠ 2 = 30 °$ ，则 $∠ B E C$ 的度数是（）

A、 $90 °$ B、 $100 °$ C、 $120 °$ D、 $110 °$

查看试题解析
8. 如图，河道l的同侧有M ， N两个村庄，计划铺设管道将河水引至M ， N两村，下面四个方案中，管道总长度最短的是（）

A、 B、 C、 D、

查看试题解析
9. 若长方形的面积是 $6 a^{3} + 9 a^{2} - 3 a b$ ，其中一边长是 $3 a$ ，则它的邻边长是（）

A、 $2 a^{3} + 3 a^{2} - b$ B、 $2 a^{2} + 3 a + b$ C、 $3 a^{2} + 2 a + b$ D、 $2 a^{2} + 3 a - b$

查看试题解析
10. 人的大脑所能记忆的内容是有限的，随着时间的推移，记忆的东西会逐渐被遗忘．德国心理学家艾宾浩斯（Hermann Ebbinghaus ， 1850－1909）第一个发现了记忆遗忘规律，他根据自己得到的测试数据描绘了一条曲线（如图所示），这就是非常有名的艾宾浩斯遗忘曲线，其中竖轴表示学习中的记忆保持量，横轴表示时间，分析图象得到下列结论，其中正确的是（）

A、记忆后0~2小时比2~4小时的遗忘速度慢 B、记忆保持量下降到 $50 %$ 所用时间为4小时 C、点A表示记忆15小时后记忆保持量约为36% D、记忆16小时后，记忆保持量始终保持不变

查看试题解析

二、填空题

11. 计算： ${(\frac{1}{2})}^{- 1} =$ .

查看试题解析
12. 一个角等于 $30 °$ ，它的补角等于 $°$ ；

查看试题解析
13. 如图，在 $△ A B C$ 和 $△ D E F$ 中，点B ， F ， C ， E在同一直线上， $A B = D E$ ， $∠ B = ∠ E$ ，请添加一个条件，使得 $△ A B C ≌ △ D E F$ ．添加的条件可以是（只需写一个，不添加辅助线）；

查看试题解析

14. 某农科所在相同条件下进行某作物种子发芽试验，结果（部分数据）如下表所示：

种子个数n	100	200	400	600	800	1000
发芽种子个数m	94	179	361	541	721	893
发芽种子的频率表 $\frac{m}{n}$ （精确到 $0.001$ ）	$0.940$	$0.895$	$0.903$	$0.902$	$0.901$	$0.893$

则任取一粒种子，在相同条件下，估计它能发芽的概率约为（精确到 $0.01$ ）；

查看试题解析

15. 如图， $△ A B C$ 中，点D、E分别是 $A B$ 、 $B C$ 的中点，连接 $A E$ 、 $C D$ 交于点F ．当 $△ A F D$ 的面积为 $\frac{7}{2}$ 时， $△ A B C$ 的面积为．

查看试题解析

三、解答题

16. 求代数式 $(a + 1) (a - 1) - a (a - 1)$ 的值，其中 $a = 2^{0}$ ．

查看试题解析
17. 一副扑克牌共有54张，黑桃、红桃、梅花、方块各有13张，还有两张王牌．

(1)、洗匀后背面朝上放在桌面上，任意抽取1张，抽到方块的概率是；

(2)、请你解释一下，打牌的时候，你摸到大王的机会比摸到4的机会小．

查看试题解析
18. 问题：“平面内，当一个角的两边与另一个角的两边分别平行时，这两个角有怎样的数量关系？”

(1)、小明阅读问题后，画出了一个如图所示的图形（已知 $A B ∥ E D$ ， $B C ∥ E F$ ），在这个图形中， $∠ B$ 与 $∠ E$ 之间的数量关系是什么？试说明理由．

(2)、当一个角的两边与另一个角的两边分别平行时，若其中一个角的度数是 $40 °$ ，那么另一个角的度数是．

查看试题解析
19. 生活中的数学：

(1)、如图1，一扇窗户打开后，用窗钩 $A B$ 可将其固定，这里所运用的几何知识是；

(2)、如图2，把小河里的水引到田地A处，若要使水沟最短，则过点A向河岸l作垂线，垂足为点B ．沿 $A B$ 挖水沟即可，这里所运用的几何知识是；

(3)、如图3，要测量池塘沿岸上两点A、E之间的距离，可以在池塘周围取两条互相平行的线段 $A B$ 和 $C D$ ，且 $A B = C D$ ，点E是线段 $B C$ 的中点，要想知道A、E之间的距离，只需要测出线段 $D E$ 的长度，这样做合适吗？请说明理由．

查看试题解析
20. 实验人员为了解某型号汽车耗油量，在公路上做了试验，并将试验数据记录下来，制成下表：
汽车行驶时间 $t (h)$
0
1
2
3
4
……
油箱剩余油量 $Q (L)$
50
44
38
32
26
……

(1)、根据上表数据，汽车出发时油箱共有油 $L$ ，当汽车行驶 $5 h$ ，油箱的剩余油量是 $L$ ；

(2)、油箱剩余油量Q与汽车行驶时间t之间的关系式是；

(3)、当剩余油量为 $2 L$ 时，汽车将自动提示加油，请问行驶几小时汽车将会自动提示加油？

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C$ ．

(1)、求作： $∠ A B C$ 的角平分线交 $A C$ 于点E ．（要求：尺规作图，保留作图痕迹，不写作法）

(2)、在（1）的条件下，若 $A E = B E$ ，求 $∠ A$ 的度数．

查看试题解析
22. 将完全平方公式作适当变形，可以用来解决很多数学问题．

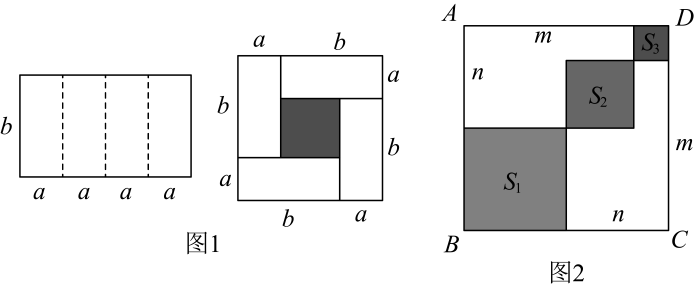(1)、观察图1，写出代数式 ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ， $a b$ 之间的等量关系：；

(2)、若 $x + y = 6$ ， $x y = 4$ ，则 $x^{2} + y^{2} =$ ； ${(x - y)}^{2} =$ ；

(3)、如图2，边长为5的正方形 $A B C D$ 中放置两个长和宽分别为m ， n（ $m < 5$ ， $n < 5$ ）的长方形，若长方形的周长为12，面积为 $8.5$ ，求图中阴影部分的面积 $S_{1} + S_{2} + S_{3}$ 的值．

查看试题解析
23. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，直线l经过点A ，过点B、C分别作l的垂线，垂足分别为点D、E ．

(1)、【特例体验】
如图1，若直线 $l ∥ B C$ ， $B D = 1$ ，则线段 $D E$ 的长为．

(2)、【探究应用】
如图2，若直线l从图1状态开始绕点A顺时针旋转 $α (0 ° < α < 45 °)$ 时，线段 $B D$ 、 $C E$ 和 $D E$ 的数量关系是；

(3)、如图3，若直线l从图1状态开始绕点A顺时针旋转 $α (45 ° < α < 90 °)$ 时与线段 $B C$ 相交，探究线段 $B D$ 、 $C E$ 和 $D E$ 的数量关系并说明理由

(4)、若 $B D = a$ ， $C E = b$ （a ， b均为正数），请你直接写出以点B、D、C、E为顶点的四边形的面积．

查看试题解析

汽车行驶时间 $t (h)$	0	1	2	3	4	……
油箱剩余油量 $Q (L)$	50	44	38	32	26	……