广西壮族自治区梧州市岑溪市2022-2023学年八年级下学期数学期末试题
试卷更新日期:2023-08-07 类型:期末考试
一、选择题(本大题共12小题:每小题3分,共36分,在每小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错,不选或多选均得0分.)
-
1. 若在实数范围内有意义,则实数的取值范围是( )A、 B、 C、 D、2. 下列计算中,正确的是( )A、 B、 C、 D、3. 三角形的三边满足 , 则此三角形是( )A、直角三角形 B、等腰直角三角形 C、等腰三角形 D、无法判断4. 已知四边形 , 下列条件中不能确定四边形是平行四边形的是( )A、且 B、且 C、且 D、且5. 关于的一元二次方程无实数根,则实数的取值范围是( )A、 B、 C、 D、6. 若是一元二次方程的两根,则的值是( )A、 B、1 C、5 D、7. 一个正多边形的每个内角都等于 , 那么它是( )A、正六边形 B、正十边形 C、正八边形 D、正十二边形8. 若 的两边长a,b满足 ,则第三边的长是( )A、5 B、 C、5或7 D、5或9. 菱形具有而矩形不一定具有的性质是 ( )
A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补10. 甲、乙、丙、丁四名学生参加市中小学生运动会跳高项目预选赛,他们8次跳高的平均成绩及方差如表所示,要选一位成绩较好且稳定的运动员去参赛,应选运动员( )甲
乙
丙
丁
(米)
1.72
1.75
1.75
1.72
(米)
1
1.3
1
1.3
A、甲 B、乙 C、丙 D、丁11. 如图,在中,对角线相交于点是的中点,若 , 则的长为( ) A、3 B、6 C、9 D、1212. 如图的对角线与相交于点 . 若 , 则的长是( )
A、3 B、6 C、9 D、1212. 如图的对角线与相交于点 . 若 , 则的长是( ) A、8 B、 C、10 D、
A、8 B、 C、10 D、二、填空题(本大题共6小题,每小题2分,共12分.)
-
13. 一组数据:2,3,4,5,6;则这组数据的方差是 .14. 有一组勾股数,其中的两个分别是8和17,则第三个数是15. 用一条长40cm的绳子围成一个面积为64cm2的矩形.设矩形的一边长为xcm,则可列方程为 .16. 如图,在平行四边形 中,添加一个条件 , 使平行四边形 是矩形.
 17. 是整数,则正数的最小值是 .18. 如图,菱形的周长为 , 则 .
17. 是整数,则正数的最小值是 .18. 如图,菱形的周长为 , 则 .
三、解答题(本大题共8小题,共72分.)
-
19. 计算:20. 解方程:21. 如图,在四边形中, , , , , 垂足分别为 , .
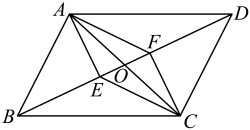 (1)、求证:;(2)、若与交于点 , 求证: .22. 如图所示,一个梯子长2.5米,顶端靠墙上,这时梯子下端与墙角的距离为1.5米,梯子滑动后停在上的位置上,如图,测得的长0.5米,求梯子顶端下落了多少米?
(1)、求证:;(2)、若与交于点 , 求证: .22. 如图所示,一个梯子长2.5米,顶端靠墙上,这时梯子下端与墙角的距离为1.5米,梯子滑动后停在上的位置上,如图,测得的长0.5米,求梯子顶端下落了多少米? 23. 已知在中,是边上的中线,四边形是平行四边形.
23. 已知在中,是边上的中线,四边形是平行四边形. (1)、求证:四边形是矩形;(2)、求矩形的面积.24. 小明同学参加周末社会实践活动,到“绿云村”蔬菜大棚中收集20株西红柿秧上小西红柿的个数:32,39,45,55,60,54,60,28,56,41,51,36,44,46,40,53,37,47,45,46.
(1)、求证:四边形是矩形;(2)、求矩形的面积.24. 小明同学参加周末社会实践活动,到“绿云村”蔬菜大棚中收集20株西红柿秧上小西红柿的个数:32,39,45,55,60,54,60,28,56,41,51,36,44,46,40,53,37,47,45,46.分组
频数
2
 (1)、前10株西红柿秧上小西红柿个数的平均数是 , 中位数是 , 众数是;(2)、若将这20个数据按组距为8进行分组,请补全频数分布表及频数直方图;(3)、通过频数直方图试分析此大棚中西红柿的长势.25. 我市某中学响应习总书记“足球进校园”的号召,开设了“足球大课间”活动,现需要购进100个某品牌的足球供学生使用,经调查,该品牌足球2021年的单价是200元,今年的单价为162元.(1)、求2021年到今年该品牌足球单价平均每年降低的百分率;(2)、购买期间发现该品牌足球在A、B两个体育用品店有不同的促销方案,A店买十送一,B店全场九折,通过计算说明到哪个店购买足球更优惠.26. 四边形 , 点分别是边的中点.
(1)、前10株西红柿秧上小西红柿个数的平均数是 , 中位数是 , 众数是;(2)、若将这20个数据按组距为8进行分组,请补全频数分布表及频数直方图;(3)、通过频数直方图试分析此大棚中西红柿的长势.25. 我市某中学响应习总书记“足球进校园”的号召,开设了“足球大课间”活动,现需要购进100个某品牌的足球供学生使用,经调查,该品牌足球2021年的单价是200元,今年的单价为162元.(1)、求2021年到今年该品牌足球单价平均每年降低的百分率;(2)、购买期间发现该品牌足球在A、B两个体育用品店有不同的促销方案,A店买十送一,B店全场九折,通过计算说明到哪个店购买足球更优惠.26. 四边形 , 点分别是边的中点. (1)、如图1,顺次连结得到四边形 , 试猜想四边形的形状并证明;(2)、如图2,若 , 顺次连结得到四边形 , 试猜想四边形的形状并证明.
(1)、如图1,顺次连结得到四边形 , 试猜想四边形的形状并证明;(2)、如图2,若 , 顺次连结得到四边形 , 试猜想四边形的形状并证明.