广东省揭阳市揭东区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-07 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，以下四个图标中可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $a > b$ ，则下列式子中正确的是（）

A、 $\frac{a}{2} < \frac{b}{2}$ B、 $a - 3 < b - 3$ C、 $- 3 a < - 3 b$ D、 $b > a$

查看试题解析
3. 已知等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为（）

A、11 B、12 C、15 D、12或15

查看试题解析
4. 式子 $n^{2} - 1$ 与 $n^{2} + n$ 的公因式是（）

A、 $n + 1$ B、 $n^{2}$ C、 $n$ D、 $n - 1$

查看试题解析
5. 化简： $\frac{x^{2}}{x^{2} - 4} \div \frac{x}{x - 2} =$ （）

A、1 B、x C、 $\frac{x}{x - 2}$ D、 $\frac{x}{x + 2}$

查看试题解析
6. 到三角形三个顶点的距离都相等的点是（）

A、两条中线的交点 B、两条高的交点 C、两条角平线的交点 D、两条边的垂直平分线的交点

查看试题解析
7. 下列各式从左到右的变形中，为因式分解的是（）

A、 $m (x + y) = m x + m y$ B、 $x^{2} + 16 x + 64 = {(x + 8)}^{2}$ C、 $x^{2} + y^{2} - 36 = x^{2} + (y + 6) (y - 6)$ D、 $a y + b y + c = y (a + b) + c$

查看试题解析
8. 如图，在 $△ A B C$ 中， $A B$ 边上的垂直平分线分别交边 $A C$ 于点 $E$ ，交边 $A B$ 于点 $D$ ，若 $A C$ 的长为 $9 c m$ ， $B E$ 的长为 $6 c m$ ，则 $E C$ 的长为（）

A、 $2 c m$ B、 $3 c m$ C、 $4 c m$ D、 $5 c m$

查看试题解析
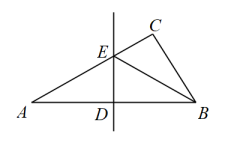9. 如果关于x的分式方程 $\frac{m}{x - 3} - \frac{1}{3 - x} = 2$ 有增根，则m的值为（）

A、1 B、 $- 1$ C、2 D、4

查看试题解析
10. 数形结合是解决数学问题常用的思想方法.如图，一次函数y＝kx+b（k、b为常数，且k＜0）的图象与直线y＝ $\frac{1}{3}$ x都经过点A（3，1），当kx+b＜ $\frac{1}{3}$ x时，x的取值范围是（）

A、x＞3 B、x＜3 C、x＜1 D、x＞1

查看试题解析

二、填空题

11. 分解因式： $18 - 2 m^{2}$ ．

查看试题解析
12. 一个多边形的内角和是它的外角和的5倍，则这个多边形的边数为。

查看试题解析
13. 如图， $△ A B C$ 沿 $B C$ 所在直线向右平移得到 $△ D E F$ ，已知 $E C = 2$ ， $B C = 5$ ，则平移的距离为．

查看试题解析
14. 点 $P (x - 1 ， x + 1)$ 在第二象限，则整数x的值是．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ B = 90 ° ， A D$ 平分 $∠ B A C$ ，若 $A C = 6 ， B D = 2$ ，则 $△ A C D$ 的面积是．

查看试题解析

三、解答题

16. 解不等式组： ${\begin{array}{l} 3 x \leq x + 4 \\ \frac{x - 2}{3} - 2 x < 1 \end{array}$ ，并写出它的所有非负整数解．

查看试题解析
17. 先化简，再求值： $(1 + \frac{1}{x - 2}) \div \frac{x^{2} - 1}{2 x - 4}$ ，其中 $x = 3$ .

查看试题解析
18. 如图，在平面直角坐标系中，一个三角板 $A B C$ 的三个顶点分别是 $A (- 3 ， 2) ， B (0 ， 4) ， C (0 ， 2)$ ．

(1)、操作与实践：
①步骤一：将三角板 $A B C$ 以点 $C$ 为旋转中心旋转 $180 °$ ，画出旋转后对应的 $△ A_{1} B_{1} C$ ；
②步骤二：平移三角板 $A B C$ ，点 $A$ 的对应点 $A_{2}$ 的坐标为 $(1 ， - 4)$ ，画出平移后对应的 $△ A_{2} B_{2} C_{2} ．$ 要求：不写作法，保留作图痕迹

(2)、应用与求解：
将 $△ A_{1} B_{1} C$ 绕某一点旋转可以得到 $△ A_{2} B_{2} C_{2}$ ，请直接写出旋转中心的坐标．

查看试题解析
19. 疫情过后，今年云南旅游市场强劲复苏．某旅行社今年春节租用A、B两种客房，用 $4800$ 元租到A客房的数量与用 $4200$ 元租到B客房的数量相同，今年每间A客房的租金比每间B客房的租金多 $30$ 元，分别求今年该旅行社租用的A、B两种客房每间客房的租金．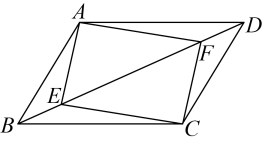

查看试题解析
20. 如图，已知点 $E$ 、 $F$ 为▱ $A B C D$ 对角线 $B D$ 上两点，且 $∠ B A F = ∠ D C E$ ，连接 $A E$ ， $C F ．$ 求证：

(1)、 $A F = C E$ ；

(2)、四边形 $A E C F$ 为平行四边形．

查看试题解析

21. 在学习对复杂多项式进行因式分解时，老师示范了如下例题：

例：因式分解： $(x^{2} + 6 x + 5) (x^{2} + 6 x - 7) + 36$

解：设 $x^{2} + 6 x = y$

原式 $= (y + 5) (y - 7) + 36$ 第一步

$= y^{2} - 2 y + 1$ 第二步

$= (y - 1)^{2}$ 第三步

$= (x^{2} + 6 x - 1)^{2}$ 第四步

完成下列任务：

(1)、例题中第二步到第三步运用了因式分解的；(填序号)

①提取公因式；②平方差公式；③两数和的完全平方公式；④两数差的完全平方公式；

(2)、请你模仿以上例题分解因式：

(a^{2} - 4 a + 2) (a^{2} - 4 a + 6) + 4

．

查看试题解析

22. 已知，在等边三角形 $A B C$ 中，点E在 $A B$ 上，点D在 $C B$ 的延长线上，且 $E D = E C$ ．

(1)、【特殊情况，探索结论】如图1，当点E为 $A B$ 的中点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你直接写出结论： $A E$ $D B$ （填“＞”、“＜”或“＝”）．

(2)、【特例启发，解答题目】如图2，当点E为 $A B$ 边上任意一点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你写出结论，并说明理由． $A E$ ▲ $D B$ （填“＞”、“＜”或“＝”）；理由如下，过点E作 $E F ∥ B C$ ，交 $A C$ 于点F ．（请你完成以下解答过程）．

(3)、【拓展结论，设计新题】在等边三角形 $A B C$ 中，点E在直线 $A B$ 上，点D在线段 $C B$ 的延长线上，且 $E D = E C$ ，若 $△ A B C$ 的边长为1， $A E = 2$ ，求 $C D$ 的长（直接写出结果）．

查看试题解析
23. 如图， $A M$ 是 $△ A B C$ 的中线， $D$ 是线段 $A M$ 上一点（不与点 $A$ 重合）． $D E ∥ A B$ 交 $A C$ 于点 $F$ ， $C E ∥ A M$ ，连接 $A E$ ．

(1)、如图1，当点 $D$ 与 $M$ 重合时，证明 $△ A B D ≌ △ E D C$ ；

(2)、如图1，当点 $D$ 与 $M$ 重合时，求证：四边形 $A B D E$ 是平行四边形；

(3)、如图2，当点 $D$ 不与 $M$ 重合时，（2）中的结论还成立吗？请说明理由．

查看试题解析