广东省汕头市金平区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-07 类型：期末考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x + 1}$ 有意义，则x应满足（）

A、 $x \geq - 1$ B、 $x \leq - 1$ C、x＞1 D、x＜1

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{5} = \sqrt{15}$ C、 $\sqrt{24} \div \sqrt{6} = 4$ D、 $3 \sqrt{3} - \sqrt{3} = 3$

查看试题解析
3. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{13}$ D、 $\sqrt{0.2}$

查看试题解析
4. 满足下列条件的 $△ A B C$ 是直角三角形的是（）

A、8，10，7 B、2，3，4 C、5，12，14 D、1， $\sqrt{3}$ ， 2

查看试题解析
5. 一次函数y=﹣2x+1的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 甲、乙、丙、丁四人进行射击测试，他们在相同条件下各射击10次，成绩（单位：环）统计如表：

甲
乙
丙
丁
平均数
9.6
9.5
9.5
9.6
方差
0.28
0.27
0.25
0.25
若从这四人中，选出一位成绩较好且状态稳定的选手参加比赛，那么应选（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 正方形具有而矩形不一定有的性质是（）

A、对角线互相垂直 B、对角线相等 C、对角互补 D、四个角相等

查看试题解析
8. 菱形 $A B C D$ 中， $∠ B A D ＝ 60 °$ ，边长为 $4$ ，则对角线 $A C$ 的长为（）

A、4 B、 $4 \sqrt{2}$ C、 $4 \sqrt{3}$ D、8

查看试题解析
9. 如图，在 $Δ A B C$ 中， $D ， E$ 分别是 $A B ， B C$ 的中点，点F在 $D E$ 延长线上，添加一个条件使四边形 $A D F C$ 为平行四边形，则这个条件是（）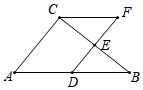

A、 $∠ B = ∠ F$ B、 $∠ B = ∠ B C F$ C、 $A C = C F$ D、 $A D = C F$

查看试题解析
10. 如图，在边长为2的正方形 $A B C D$ 中，点P从点A出发，沿A→B→C→D匀速运动到点D ，若点E是BC的中点，则 $△ A P E$ 的面积y与点P运动的路程x之间形成的函数关系图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 计算 $\sqrt{3} \times \sqrt{8} =$ ．

查看试题解析
12. 某医院开展了主题为“抗击疫情，迎战硝烟”的护士技能比赛活动，决赛中5名护士的成绩（单位：分）分别为：88，93，90，93，92，则这组数据的中位数是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $A D = D C$ ， $B D = 4$ ，则 $A C =$ ．

查看试题解析
14. 一次函数 $y = 2 x$ 和 $y = a x + 4$ 的图象相交于点 $A (m ， 3)$ ．则不等式 $a x + 4 < 2 x$ 的解集是．

查看试题解析
15. 如图，在 $R t △ A B C$ 中，斜边 $A B = 4$ ， $∠ B A C = 30 °$ ， $A B$ 的垂直平分线分别交 $A B$ 、 $A C$ 于点E、点D ，连接 $B D$ ，点M ， N分别是 $B D$ 和 $B C$ 上的动点，则 $C M + M N$ 的最小值是．

查看试题解析

三、解答题

16. 计算： $\sqrt{24} \times \sqrt{6} \div 3 \sqrt{2} - \sqrt{\frac{1}{8}} \times (1 - \sqrt{2})^{0}$ ．

查看试题解析
17. 某条道路限速 $80 k m / h$ ，如图，一辆小汽车在这条道路上沿直线行驶，某一时刻刚好行驶到路对面车速检测仪A处的正前方 $30 m$ 的C处，过了 $2 s$ ，小汽车到达B处，此时测得小汽车与车速检测仪间的距离为 $50 m$ ．

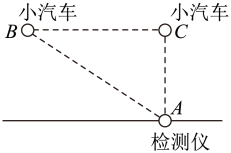(1)、求 $B C$ 的长；

(2)、这辆小汽车超速了吗？

查看试题解析
18. 张青、李红和小明三人在讨论课本的一道题：
如图，在平行四边形 $A B C D$ 中，E、F是对角线 $A C$ 上的两点， $A E = C F$ ．

求证：四边形 $B E D F$ 是平行四边形．

张青说：“要证明三角形全等才能解决问题．”

李红说：“不对，只要连接 $B D$ ，不用证明三角形全等也能解决问题．”

小明问老师他们谁是对的？

老师说：“李红说得对．”并要求小明按李红的思路完成这题目．

请你帮小明写出完整的证明过程．

查看试题解析
19. 为了了解某校新初三暑期阅读课外书的情况，某研究小组随机采访该校新九年级的20位同学，得到这20位同学暑期读课外书册数的统计如下：

册数

0

2

3

5

6

8

10

人数

1

2

4

8

2

2

1

(1)、这20位同学暑期看课外书册数的中位数是册，众数是册，平均数是册。

(2)、若小明同学把册数中的数据“8”看成了“7”，那么中位数，众数，平均数中不受影响的是。

(3)、若该校有600名新初三学生，试估计该校新初三学生暑期阅读课外书的总册数。

查看试题解析
20. 阅读材料，并解决问题：定义：将分母中的根号化去的过程叫做分母有理化．
如：将 $\frac{1}{\sqrt{3} - \sqrt{2}}$ 分母有理化，解：原式 $= \frac{\sqrt{3} + \sqrt{2}}{(\sqrt{3} - \sqrt{2}) (\sqrt{3} + \sqrt{2})} = \sqrt{3} + \sqrt{2}$ ．
运用以上方法解决问题：
已知： $a = \frac{1}{\sqrt{5} + 2}$ ， $b = \frac{1}{\sqrt{5} - 2}$ ．

(1)、化简a ， b；

(2)、求 $a^{2} - 4 a b + b^{2}$ 的值．

查看试题解析
21. 如图，直线 $y = \frac{4}{3} x + 8$ 和直线 $y = k x + b$ 都经过x轴负半轴上一点B ，分别与y轴的交点分别为A、C ，且 $O B = 2 O C$ ．

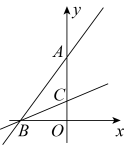(1)、求直线 $C B$ 的解析式；

(2)、点E在x轴上， $△ A B E$ 为等腰三角形，请直接写出点E的坐标．

查看试题解析
22. 如图，点 $E$ 在正方形 $A B C D$ 对角线 $B D$ 上，连接 $A E 、 C E$ ，点 $F$ 为 $A B$ 上一点，连接 $C F$ ，交 $B D$ 于点 $G$ ．连接 $E F$ ，若 $A E = E F$ ．

(1)、求证： $A E = C E$ ；

(2)、求 $∠ E C F$ 的度数；

(3)、经探究， $D E$ 、 $B G$ 、 $E G$ 三条线段满足某种数量关系，请直接写出它们之间的关系式．

查看试题解析
23. 如图，平面直角坐标系中， $A (0 ， 4)$ ， $C (8 ， 0)$ ． F为矩形 $O A B C$ 对角线 $A C$ 的中点，过点F的直线分别与 $O C 、 A B$ 交于点D、E ．

(1)、求证： $F D = F E$ ；

(2)、设 $O D = m$ ， $△ A D F$ 的面积为S ，
①求S与m的函数关系式；
②当 $D E ⊥ A C$ 时，求S的值；

(3)、若点P在坐标轴上，平面内存在点Q ，使以P、Q、A、C为顶点的四边形是矩形，请直接写出点Q的坐标．

查看试题解析

	甲	乙	丙	丁
平均数	9.6	9.5	9.5	9.6
方差	0.28	0.27	0.25	0.25

册数	0	2	3	5	6	8	10
人数	1	2	4	8	2	2	1