广东省汕头市潮南区两英镇2022-2023学年八年级下学期期末数学试题(A)
试卷更新日期:2023-08-07 类型:期末考试
一、单选题
-
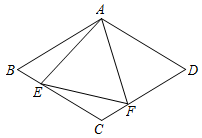
1. 函数中,自变量的取值范围是( )A、 B、 C、 D、全体实数2. 如果是最简二次根式,则x的值可能是( )A、11 B、13 C、21 D、273. 如图,四边形是平行四边形,其对角线 , 相交于点 , 下列理论一定成立的是( )
 A、 B、 C、 D、4. 对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )A、平均数是1 B、众数是-1 C、中位数是0.5 D、方差是3.55. 当时,代数式的值是( )A、23 B、24 C、25 D、266. 如图,在中, . 分别以点为圆心,以长为半径画弧,两弧相交于点 , 连接 , 则的周长为( )
A、 B、 C、 D、4. 对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )A、平均数是1 B、众数是-1 C、中位数是0.5 D、方差是3.55. 当时,代数式的值是( )A、23 B、24 C、25 D、266. 如图,在中, . 分别以点为圆心,以长为半径画弧,两弧相交于点 , 连接 , 则的周长为( ) A、9 B、12 C、 D、157. 如图,在中,平分 , 若 , 则的面积为( )
A、9 B、12 C、 D、157. 如图,在中,平分 , 若 , 则的面积为( ) A、6 B、18 C、24 D、328. 在长方形ABCD中, , , 连接AC , 的角平分线交BC于点E , 则线段BE的长为( )
A、6 B、18 C、24 D、328. 在长方形ABCD中, , , 连接AC , 的角平分线交BC于点E , 则线段BE的长为( ) A、 B、 C、3 D、49. 如图,一次函数的图象与轴、轴分别交于点点 , 过点作直线将分成周长相等的两部分,则直线的函数表达式为( )
A、 B、 C、3 D、49. 如图,一次函数的图象与轴、轴分别交于点点 , 过点作直线将分成周长相等的两部分,则直线的函数表达式为( ) A、 B、 C、 D、10. 如图,在中, , , , 点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN , MN的中点,则DE的最小值是( )
A、 B、 C、 D、10. 如图,在中, , , , 点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN , MN的中点,则DE的最小值是( ) A、2 B、 C、3 D、
A、2 B、 C、3 D、二、填空题
-
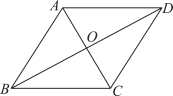
11. .12. 有一组数据如下: , , 1,3,5,则这组数据的中位数是 .13. 如图,平行四边形的对角线与相交于点 , , 垂足为 , , 则的长为 .
 14. 如图,矩形内三个相邻的正方形面积分别为4,3和2,则图中阴影部分的面积为 .
14. 如图,矩形内三个相邻的正方形面积分别为4,3和2,则图中阴影部分的面积为 . 15. 在直角坐标系中,等腰直角三角形、、、…、按如图所示的方式放置,其中点、、、…、均在一次函数的图象上,点、、、…、均在x轴上.若点的坐标为 , 点的坐标为 , 则点的坐标为 .
15. 在直角坐标系中,等腰直角三角形、、、…、按如图所示的方式放置,其中点、、、…、均在一次函数的图象上,点、、、…、均在x轴上.若点的坐标为 , 点的坐标为 , 则点的坐标为 .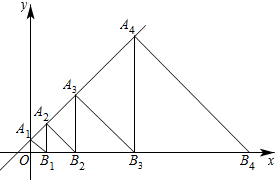
三、解答题
-
16. 计算: .17. 如果最简二次根式与能进行合并.且 , 化简: .18. 如图,在中, .
 (1)、尺规作图:作边的垂直平分线,分别交、边于点E、F(要求:保留作图痕迹,不写作法);(2)、连接 , 若 , 求的度数.19. 近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,某高校为了解本校学生出行使用共享单车的情况,随机调查了某天50名出行学生使用共享单车次数的情况,并整理如下统计表.
(1)、尺规作图:作边的垂直平分线,分别交、边于点E、F(要求:保留作图痕迹,不写作法);(2)、连接 , 若 , 求的度数.19. 近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,某高校为了解本校学生出行使用共享单车的情况,随机调查了某天50名出行学生使用共享单车次数的情况,并整理如下统计表.使用次数
1
2
3
4
5
人数
8
13
11
12
6
(1)、这50名出行学生使用共享单车次数的中位数是 , 众数是;(2)、这天中,这50名出行学生平均每人使用共享单车多少次?20. 如图,某人从A地到B地共有三条路可选,第一条路是从A到B,AB为10米,第二条路是从A经过C到达B地,AC为8米,BC为6米,第三条路是从A经过D地到B地共行走26米,若C、B、D刚好在一条直线上. (1)、求证:;(2)、求AD和BD的长.21. 如图,在中,E为BC边的中点,连接DE,并延长DE交AB的延长线于点F.
(1)、求证:;(2)、求AD和BD的长.21. 如图,在中,E为BC边的中点,连接DE,并延长DE交AB的延长线于点F. (1)、求证:四边形DBFC是平行四边形;(2)、若 , , , 求BD的长.
(1)、求证:四边形DBFC是平行四边形;(2)、若 , , , 求BD的长.