广东省汕头市澄海区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-07 类型:期末考试
一、单选题
-
1. 下列各式中是最简二次根式的是( )A、 B、 C、 D、2. 一个底面是长方形的小塑料盒,长为40cm,宽为30cm,在小塑料盒底面放一根木棒,那么这根木棒最长(不计木棒粗细)可以是( )A、30cm B、40cm C、50cm D、3. 一次函数y=﹣2x+1的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 在一次歌咏比赛中,某选手的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是( )A、94,94 B、95,95 C、94,95 D、95,945. 已知关于x的一次函数 , y值随x的增大而减小,则的值可以是( )A、2 B、1 C、 D、6. 代数式中字母x的取值范围是( )A、 B、 C、且 D、且7. 如图,在中,的平分线交于点E , 若 , 则的度数为( )
 A、112° B、116° C、128° D、148°8. 如图,在矩形中,对角线与相交于点O , 过点C作交的延长线于点E , 下列结论不一定正确的是( )
A、112° B、116° C、128° D、148°8. 如图,在矩形中,对角线与相交于点O , 过点C作交的延长线于点E , 下列结论不一定正确的是( ) A、 B、 C、是等腰三角形 D、9. 如图,矩形的边在数轴上,若点A与数轴上表示数的点重合,点D与数轴上表示数的点重合, , 以点A为圆心以对角线的长为半径作弧与数轴负半轴交于一点E , 则点E表示的数为( )
A、 B、 C、是等腰三角形 D、9. 如图,矩形的边在数轴上,若点A与数轴上表示数的点重合,点D与数轴上表示数的点重合, , 以点A为圆心以对角线的长为半径作弧与数轴负半轴交于一点E , 则点E表示的数为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,正方形的两个顶点A、B是坐标轴上的动点,若正方形的边长为4,则线段长的最大值是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,正方形的两个顶点A、B是坐标轴上的动点,若正方形的边长为4,则线段长的最大值是( )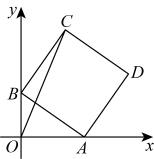 A、 B、 C、 D、8
A、 B、 C、 D、8二、填空题
-
11. 一根蜡烛长25cm,点燃后每小时燃烧5cm,蜡烛燃烧时剩下的高度 (厘米)与燃烧时间 (小时)()之间的关系是 .12. 如图,已知菱形的周长为 , , 则对角线的长为 .
 13. 计算: .14. 如图,在中, , 边上的垂直平分线与、分别交于点E和D , 若 , , 则的长为 .
13. 计算: .14. 如图,在中, , 边上的垂直平分线与、分别交于点E和D , 若 , , 则的长为 . 15. 观察下列一组数:
15. 观察下列一组数:列举:3,4,5, 猜想:32=4+5;
列举:5,12,13,猜想:52=12+13;
列举:7,24,25,猜想:72=24+25;
… …
列举:13,b , c , 猜想:132=b+c;
请你分析上述数据的规律,结合相关知识求得b= , c= .
三、解答题
-
16. 计算: .17. 如图,在四边形中, , , , , . 求四边形的面积.
 18. 在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
18. 在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)、本次调查中,一共调查了名同学;(2)、条形统计图中,m= , n=;(3)、扇形统计图中,艺术类读物所在扇形的圆心角是度;(4)、学校计划购买课外读物4000册,请根据样本数据,估计学校购买文学类读物多少册比较合理?19. 已知 , , 求下列代数式的值:(1)、;(2)、 .20. 某水果店老板购进一批优质枇杷,经调查,该枇杷每天销售量y(千克)与销售单价x(元/千克)之间符合一次函数关系(如图所示). (1)、求y与x的函数关系式;(2)、如果该老板购进的枇杷为3500千克,其保质期为20天,若以12元/千克销售,问能否在保质期内销售完这批枇杷?请说明理由.21. 如图,在中, , 点E是的中点,的平分线交于点D , 作 , 连接并延长交于点F , 连接 .
(1)、求y与x的函数关系式;(2)、如果该老板购进的枇杷为3500千克,其保质期为20天,若以12元/千克销售,问能否在保质期内销售完这批枇杷?请说明理由.21. 如图,在中, , 点E是的中点,的平分线交于点D , 作 , 连接并延长交于点F , 连接 . (1)、求证:四边形是平行四边形;(2)、当时,请判断四边形的形状,并说明理由.
(1)、求证:四边形是平行四边形;(2)、当时,请判断四边形的形状,并说明理由.

