辽宁省抚顺市、葫芦岛市2023年中考数学试卷
试卷更新日期:2023-08-07 类型:中考真卷
一、选择题(本题共10小题,每小题3分,共30分,在每一个小题给出的四个选中,只有一个是正确的)
-
1. 实数3的相反数是( )A、3 B、 C、 D、2. 下列图形中、既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、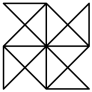 D、
D、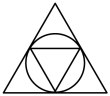 3. 下列运算正确的是( )A、 B、 C、 D、4. 下图是由5个完全相同的小正方体搭成的几何体、这个几何体的主视图是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 下图是由5个完全相同的小正方体搭成的几何体、这个几何体的主视图是( )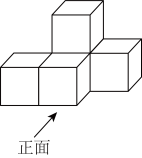 A、
A、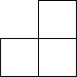 B、
B、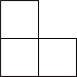 C、
C、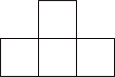 D、
D、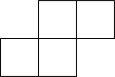 5. 某校对部分参加夏令营的中学生的年龄进行统计,结果如下表:
5. 某校对部分参加夏令营的中学生的年龄进行统计,结果如下表:年龄岁
13
14
15
16
17
18
人数/人
5
8
11
20
9
7
则这些学生年龄的众数是( )
A、13岁 B、14岁 C、15岁 D、16岁6. 在一个不透明的袋子中装有6个白球和14个红球,这些球除颜色外无其他差别、随机从袋子中摸出一个球,则摸到白球的概率为( )A、 B、 C、 D、7. 如图,直线 , 被直线所截, , , 则的度数为( ) A、48° B、58° C、68° D、78°8. 《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天:如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为天,则可列方程为( )A、 B、 C、 D、9. 如图,在中, , , , 按以下步骤作图:①分别以点A和点B为圆心,大于长为半径作弧,两弧相交于E , F两点;②作直线交于点M , 交于点N . 连接 . 则的长为( )
A、48° B、58° C、68° D、78°8. 《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天:如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为天,则可列方程为( )A、 B、 C、 D、9. 如图,在中, , , , 按以下步骤作图:①分别以点A和点B为圆心,大于长为半径作弧,两弧相交于E , F两点;②作直线交于点M , 交于点N . 连接 . 则的长为( )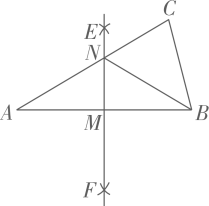 A、 B、 C、 D、10. 如图, , 在射线 , 上分别截取 , 连接 , 的平分线交于点D , 点E为线段上的动点,作交于点F , 作交射线于点G , 过点G作于点H , 点E沿方向运动,当点E与点B重合时停止运动.设点E运动的路程为x , 四边形与重叠部分的面积为S , 则能大致反映S与x之间函数关系的图象是( )
A、 B、 C、 D、10. 如图, , 在射线 , 上分别截取 , 连接 , 的平分线交于点D , 点E为线段上的动点,作交于点F , 作交射线于点G , 过点G作于点H , 点E沿方向运动,当点E与点B重合时停止运动.设点E运动的路程为x , 四边形与重叠部分的面积为S , 则能大致反映S与x之间函数关系的图象是( )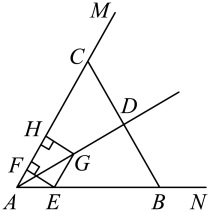 A、
A、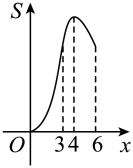 B、
B、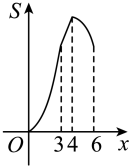 C、
C、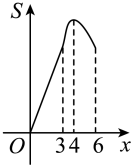 D、
D、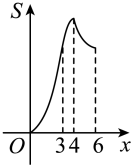
二、填空题(本题共8个小题,每小题3分,共24分)
-
11. 若有意义,则实数a的取值范围是 .12. 分解因式: .13. 若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .14. 某跳远队准备从甲、乙两名运动员中选取一名成绩稳定的参加比赛,这两名运动员10次测试成绩(单位:m)的平均数是 , , 方差是 , , 那么应选去参加比赛.(填“甲”或“乙”)15. 如图,在中, , 点D为的中点,过点C作交的延长线于点E , 若 , , 则的长为 .
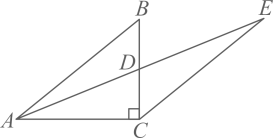 16. 如图,在平面直角坐标系中,点的坐标为 , 将线段绕点逆时针旋转 , 得到线段 , 连接 , 点恰好落在反比例函数()的图象上,则的值是 .
16. 如图,在平面直角坐标系中,点的坐标为 , 将线段绕点逆时针旋转 , 得到线段 , 连接 , 点恰好落在反比例函数()的图象上,则的值是 .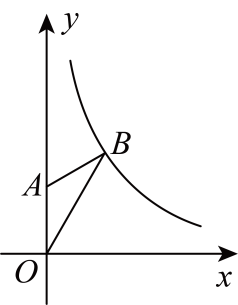 17. 如图,平行四边形的对角线 , 相交于点 , 过点作 , 交的延长线于点E,连接 , 交于点 , 则四边形的面积与的面积的比值为 .
17. 如图,平行四边形的对角线 , 相交于点 , 过点作 , 交的延长线于点E,连接 , 交于点 , 则四边形的面积与的面积的比值为 .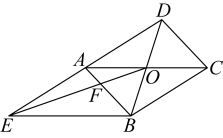 18. 如图,在矩形中, , , 点M为的中点,E是上的一点,连接 , 作点B关于直线的对称点 , 连接并延长交于点F . 当最大时,点到的距离是 .
18. 如图,在矩形中, , , 点M为的中点,E是上的一点,连接 , 作点B关于直线的对称点 , 连接并延长交于点F . 当最大时,点到的距离是 .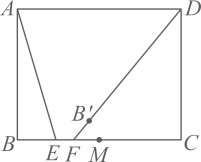
三、解答题(共8题,共96分)
-
19. 先化简,再求值: , 其中 .20. 为了推进“优秀传统文化进校园”活动,学校准备在七年级成立四个课外活动小组,分别是: . 民族舞蹈组; . 经典诵读组; . 民族乐器组; . 地方戏曲组.为了了解学生最喜欢哪一个活动小组,学校从七年级全体学生中随机抽取部分学生进行问卷调查,每人必须选择且只能选择一项,并将调查结果绘制成如下两幅统计图.
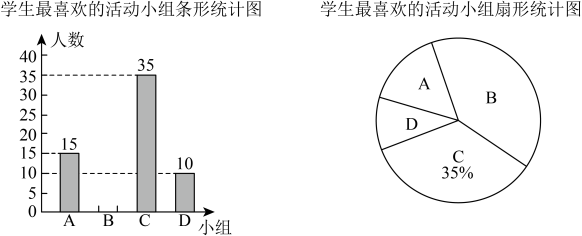
请根据图中提供的信息解答下列问题:
(1)、本次调查的学生共有人;(2)、在扇形统计图中,求组所对应的扇形圆心角的度数,并补全条形统计图;(3)、在重阳节来临之际,学校计划组织学生到敬老院为老人表演节目,准备从这个小组中随机抽取个小组汇报演出,请你用列表法或画树状图法,求选中的个小组恰好是和小组的概率.21. 某超市销售甲、乙两种驱蚊手环,某天卖出3个甲种驱蚊手环和1个乙种驱蚊手环,收入128元;另一天,以同样的价格卖出1个甲种驱蚊手环和2个乙种驱蚊手环收入76元.(1)、每个甲种驱蚊手环和每个乙种驱蚊手环的售价分别是多少元?(2)、某幼儿园欲购买甲、乙两种驱蚊手环共100个,总费用不超过2500元,那么最多可购买甲种驱蚊手环多少个?22. 小亮利用所学的知识对大厦的高度进行测量,他在自家楼顶B处测得大厦底部的俯角是 , 测得大厦顶部的仰角是 , 已知他家楼顶B处距地面的高度为40米(图中点A , B , C , D均在同一平面内).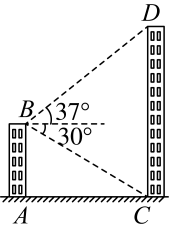 (1)、求两楼之间的距离(结果保留根号);(2)、求大厦的高度(结果取整数).
(1)、求两楼之间的距离(结果保留根号);(2)、求大厦的高度(结果取整数).(参考数据: , , , )
23. 电商平台销售某款儿童组装玩具,进价为每件100元,在销售过程中发现,每周的销售量y(件)与每件玩具售价x(元)之间满足一次函数关系(其中 , 且x为整数).当每件玩具售价为120元时,每周的销量为80件;当每件玩具售价为140元时,每周的销量为40件.(1)、求y与x之间的函数关系式;(2)、当每件玩具售价为多少元时,电商平台每周销售这款玩具所获的利润最大?最大周利润是多少元?24. 如图,内接于 , 是的直径,平分交于点E , 过点E作 , 交的延长线于点F .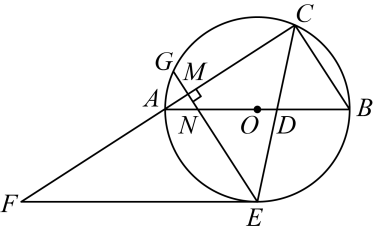 (1)、求证:与相切;(2)、若 , , 过点E作于点M , 交于点G , 交于点N , 求的长.25. 是等边三角形,点是射线上的一点(不与点 , 重合),连接 , 在的左侧作等边三角形 , 将线段绕点逆时针旋转 , 得到线段 , 连接 . 交于点 .
(1)、求证:与相切;(2)、若 , , 过点E作于点M , 交于点G , 交于点N , 求的长.25. 是等边三角形,点是射线上的一点(不与点 , 重合),连接 , 在的左侧作等边三角形 , 将线段绕点逆时针旋转 , 得到线段 , 连接 . 交于点 . (1)、如图1,当点为中点时,请直接写出线段与的数量关系;(2)、如图2.当点在线段的延长线上时,请判断()中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、当 , 时,请直接写出的长.26. 如图,抛物线与x轴交于点A和点 , 与y轴交于点 , 点P为第一象限内抛物线上的动点过点P作轴于点E,交于点F.
(1)、如图1,当点为中点时,请直接写出线段与的数量关系;(2)、如图2.当点在线段的延长线上时,请判断()中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、当 , 时,请直接写出的长.26. 如图,抛物线与x轴交于点A和点 , 与y轴交于点 , 点P为第一象限内抛物线上的动点过点P作轴于点E,交于点F.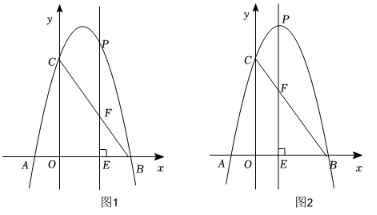 (1)、求抛物线的解析式;(2)、如图1,当的周长是线段长度的2倍时,求点P的坐标;(3)、如图2,当点P运动到抛物线顶点时,点Q是y轴上的动点,连接 , 过点B作直线 , 连接并延长交直线于点M.当时,请直接写出点Q的坐标.
(1)、求抛物线的解析式;(2)、如图1,当的周长是线段长度的2倍时,求点P的坐标;(3)、如图2,当点P运动到抛物线顶点时,点Q是y轴上的动点,连接 , 过点B作直线 , 连接并延长交直线于点M.当时,请直接写出点Q的坐标.