宁夏回族自治区2023年数学中考试卷
试卷更新日期:2023-08-07 类型:中考真卷
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、2. 下面是由七巧板拼成的图形(只考虑外形,忽略内部轮廓),其中轴对称图形是( )
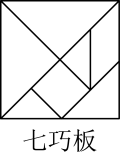 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 劳动委员统计了某周全班同学的家庭劳动次数(单位:次),按劳动次数分为4组: , , , , 绘制成如图所示的频数分布直方图.从中任选一名同学,则该同学这周家庭劳动次数不足6次的概率是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 劳动委员统计了某周全班同学的家庭劳动次数(单位:次),按劳动次数分为4组: , , , , 绘制成如图所示的频数分布直方图.从中任选一名同学,则该同学这周家庭劳动次数不足6次的概率是( )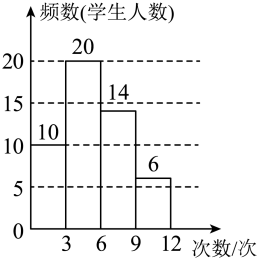 A、 B、 C、 D、5. 估计的值应在( )A、和4之间 B、4和之间 C、和5之间 D、5和之间6. 将一副直角三角板和一把宽度为2cm的直尺按如图方式摆放:先把和角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上,这两个三角板的斜边分别交直尺上沿于 , 两点,则的长是( )
A、 B、 C、 D、5. 估计的值应在( )A、和4之间 B、4和之间 C、和5之间 D、5和之间6. 将一副直角三角板和一把宽度为2cm的直尺按如图方式摆放:先把和角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上,这两个三角板的斜边分别交直尺上沿于 , 两点,则的长是( ) A、 B、 C、2 D、7. 在同一平面直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( )
A、 B、 C、2 D、7. 在同一平面直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( ) A、随的增大而增大 B、 C、当时, D、关于 , 的方程组的解为8. 如图,在中, , , . 点在上,且 . 连接 , 将线段绕点顺时针旋转得到线段 , 连接 , . 则的面积是( )
A、随的增大而增大 B、 C、当时, D、关于 , 的方程组的解为8. 如图,在中, , , . 点在上,且 . 连接 , 将线段绕点顺时针旋转得到线段 , 连接 , . 则的面积是( )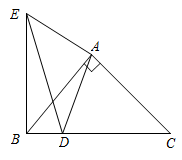 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算: .10. 如图,在边长为2的正方形中,点在上,连接 , . 则图中阴影部分的面积是 .
 11. 方程有两个相等的实数根,则的值为 .12. 如图,在标有数字1,2,3,4的四宫格里任选两个小方格,则所选方格中数字之和为4的概率是 .
11. 方程有两个相等的实数根,则的值为 .12. 如图,在标有数字1,2,3,4的四宫格里任选两个小方格,则所选方格中数字之和为4的概率是 . 13. 如图,四边形内接于 , 延长至点 , 已知 , 那么 .
13. 如图,四边形内接于 , 延长至点 , 已知 , 那么 .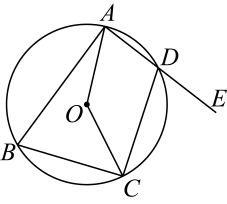 14. 如图,点 , , 在数轴上,点表示的数是 , 点是的中点,线段 , 则点表示的数是 .
14. 如图,点 , , 在数轴上,点表示的数是 , 点是的中点,线段 , 则点表示的数是 .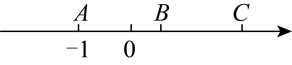 15. 如图是某种杆秤.在秤杆的点处固定提纽,点处挂秤盘,点为0刻度点.当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点 , 秤杆处于平衡.秤盘放入克物品后移动秤砣,当秤砣所挂位置与提扭的距离为毫米时秤杆处于平衡.测得与的几组对应数据如下表:
15. 如图是某种杆秤.在秤杆的点处固定提纽,点处挂秤盘,点为0刻度点.当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点 , 秤杆处于平衡.秤盘放入克物品后移动秤砣,当秤砣所挂位置与提扭的距离为毫米时秤杆处于平衡.测得与的几组对应数据如下表:/克
0
2
4
6
10
/毫米
10
14
18
22
30
由表中数据的规律可知,当克时,毫米.
 16. 如图是由边长为1的小正方形组成的网格,点 , , , , , , 均在格点上.下列结论:
16. 如图是由边长为1的小正方形组成的网格,点 , , , , , , 均在格点上.下列结论:
①点与点关于点中心对称;
②连接 , , , 则平分;
③连接 , 则点 , 到线段的距离相等.
其中正确结论的序号是 .
三、解答题
-
17. 计算:18. 解不等式组
下面是某同学的部分解答过程,请认真阅读并完成任务:
解:由①得:
第1步
第2步
第3步
第4步
任务一:该同学的解答过程第 ▲ 步出现了错误,错误原因是 ▲ , 不等式①的正确解集是 ▲ ;
任务二:解不等式②,并写出该不等式组的解集.
19. 如图,已知 , , 分别是和上的点, . 求证:四边形是平行四边形.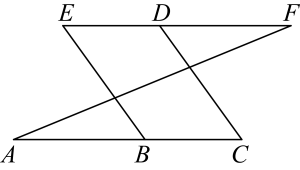 20. “人间烟火味,最抚凡人心”,地摊经济、小店经济是就业岗位的重要来源.某经营者购进了型和型两种玩具,已知用520元购进型玩具的数量比用175元购进型玩具的数量多30个,且型玩具单价是型玩具单价的倍.(1)、求两种型号玩具的单价各是多少元?
20. “人间烟火味,最抚凡人心”,地摊经济、小店经济是就业岗位的重要来源.某经营者购进了型和型两种玩具,已知用520元购进型玩具的数量比用175元购进型玩具的数量多30个,且型玩具单价是型玩具单价的倍.(1)、求两种型号玩具的单价各是多少元?根据题意,甲、乙两名同学分别列出如下方程:
甲: , 解得 , 经检验是原方程的解.
乙: , 解得 , 经检验是原方程的解.
则甲所列方程中的表示 , 乙所列方程中的表示;
(2)、该经营者准备用1350元以原单价再次购进这两种型号的玩具共200个,则最多可购进型玩具多少个?21. 给某气球充满一定质量的气体,在温度不变时,气球内气体的气压是气体体积()的反比例函数,其图象如图所示.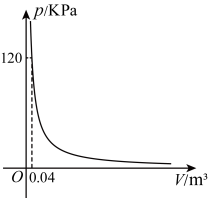 (1)、当气球内的气压超过时,气球会爆炸.若将气球近似看成一个球体,试估计气球的半径至少为多少时气球不会爆炸(球体的体积公式 , 取3);(2)、请你利用与的关系试解释为什么超载的车辆容易爆胎.22. 如图,粮库用传送带传送粮袋,大转动轮的半径为10cm,传送带与水平面成角.假设传送带与转动轮之间无滑动,当大转动轮转时,传送带上点处的粮袋上升的高度是多少?(传送带厚度忽略不计)
(1)、当气球内的气压超过时,气球会爆炸.若将气球近似看成一个球体,试估计气球的半径至少为多少时气球不会爆炸(球体的体积公式 , 取3);(2)、请你利用与的关系试解释为什么超载的车辆容易爆胎.22. 如图,粮库用传送带传送粮袋,大转动轮的半径为10cm,传送带与水平面成角.假设传送带与转动轮之间无滑动,当大转动轮转时,传送带上点处的粮袋上升的高度是多少?(传送带厚度忽略不计)
 23. 学校组织七、八年级学生参加了“国家安全知识”测试(满分100分).已知七、八年级各有200人,现从两个年级分别随机抽取10名学生的测试成绩(单位:分)进行统计:
23. 学校组织七、八年级学生参加了“国家安全知识”测试(满分100分).已知七、八年级各有200人,现从两个年级分别随机抽取10名学生的测试成绩(单位:分)进行统计:七年级 86,94,79,84,71,90,76,83,90,87
八年级 88,76,90,78,87,93,75,87,87,79
整理如下:
年级
平均数
中位数
众数
方差
七年级
84
90
八年级
84
87
根据以上信息,回答下列问题:
(1)、填空: , .同学说:“这次测试我得了86分,位于年级中等偏上水平”,由此可判断他是年级的学生;
(2)、学校规定测试成绩不低于85分为“优秀”,估计该校这两个年级测试成绩达到“优秀”的学生总人数;(3)、你认为哪个年级的学生掌握国家安全知识的总体水平较好?请给出一条理由.24. 如图,已知是的直径,直线是的切线,切点为 , , 垂足为 . 连接 . (1)、求证:平分;(2)、若 , , 求的半径.25. 如图,抛物线与轴交于 , 两点,与轴交于点 . 已知点的坐标是 , 抛物线的对称轴是直线 .
(1)、求证:平分;(2)、若 , , 求的半径.25. 如图,抛物线与轴交于 , 两点,与轴交于点 . 已知点的坐标是 , 抛物线的对称轴是直线 . (1)、直接写出点的坐标;(2)、在对称轴上找一点 , 使的值最小.求点的坐标和的最小值;(3)、第一象限内的抛物线上有一动点 , 过点作轴,垂足为 , 连接交于点 . 依题意补全图形,当的值最大时,求点的坐标.26. 综合与实践
(1)、直接写出点的坐标;(2)、在对称轴上找一点 , 使的值最小.求点的坐标和的最小值;(3)、第一象限内的抛物线上有一动点 , 过点作轴,垂足为 , 连接交于点 . 依题意补全图形,当的值最大时,求点的坐标.26. 综合与实践问题背景
数学小组发现国旗上五角星的五个角都是顶角为的等腰三角形,对此三角形产生了极大兴趣并展开探究.

探究发现
如图1,在中, , .
 (1)、操作发现:将折叠,使边落在边上,点的对应点是点 , 折痕交于点 , 连接 , , 则 , 设 , , 那么(用含的式子表示);(2)、进一步探究发现: , 这个比值被称为黄金比.在(1)的条件下试证明:;
(1)、操作发现:将折叠,使边落在边上,点的对应点是点 , 折痕交于点 , 连接 , , 则 , 设 , , 那么(用含的式子表示);(2)、进一步探究发现: , 这个比值被称为黄金比.在(1)的条件下试证明:;拓展应用:
当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图1中的是黄金三角形.如图2,在菱形中, , . 求这个菱形较长对角线的长.
 (3)、拓展应用:
(3)、拓展应用:当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图1中的是黄金三角形.如图2,在菱形中, , . 求这个菱形较长对角线的长.
