辽宁省沈阳市交联体2022-2023学年高一下学期4月月考物理试题

试卷更新日期：2023-08-07 类型：月考试卷

进入出卷网下载

一、单选题

1. 在科学发展的历程中，许多科学家做出了杰出的贡献，下列叙述符合史实的是（　　）

A、开普勒总结出了行星运动的规律，发现了万有引力定律 B、关于万有引力公式 $F = G \frac{m_{1} m_{2}}{r^{2}}$ 公式中引力常量G的值是牛顿测得的 C、相对论的出现使经典物理学在自己的适用范围内不再继续发挥作用 D、牛顿将行星与太阳、地球与月球、地球与地面物体之间的引力规律推广到宇宙中的一切物体，得出了万有引力定律

查看试题解析
2. 下列现象中属于防止离心现象带来危害的是（）

A、旋转雨伞甩掉雨伞上的水滴 B、列车转弯处铁轨的外轨道比内轨道高些 C、拖把桶通过旋转使拖把脱水 D、洗衣机脱水简高速旋转甩掉附着在衣服上的水

查看试题解析
3. 一质点做半径为R的匀速圆周运动，在t时间内转动n周，则该质点的线速度为（　　）

A、 $\frac{2 π R}{n t}$ B、 $\frac{2 π n R}{t}$ C、 $\frac{n R}{2 π t}$ D、 $\frac{2 π t}{n R}$

查看试题解析
4. $2022$ 年 $11$ 月 $27$ 日，我国在西昌卫星发射中心使用“长征二号”丁运载火箭，成功将“遥感三十六号”卫星发射升空，卫星顺利进入预定轨道，发射任务获得圆满成功。若已知该卫星在预定轨道上绕地球做匀速圆周运动，其线速度大小为 $v$ ，角速度大小为 $ω$ ，引力常量为 $G$ ，则地球的质量为（　　）

A、 $\frac{v^{3}}{G ω^{2}}$ B、 $\frac{v^{2}}{G ω}$ C、 $\frac{v^{3}}{G ω}$ D、 $\frac{v^{2}}{G ω^{2}}$

查看试题解析
5. 如图所示，长为l的轻绳，一端固定在水平转轴O上，另一端栓接质量为m的小球。现给静止于最低点的小球一初速度，使小球绕转轴O在竖直平面内运动，当绳与水平面之间的夹角为 $θ$ 时，轻绳的拉力恰好为零，重力加速度为g ，则此时小球绕转轴O运动的角速度为（　　）

A、 $\sqrt{\frac{g}{l}}$ B、 $\sqrt{\frac{g t a n θ}{l}}$ C、 $\sqrt{\frac{g c o s θ}{l}}$ D、 $\sqrt{\frac{g s i n θ}{l}}$

查看试题解析
6. 设地球自转周期为T ，质量为M ，引力常量为G。假设地球可视为质量均匀分布的球体，半径为R。同一物体在南极和赤道水平面上静止时所受到的支持力之比为（　　）

A、 $\frac{G M T^{2}}{G M T^{2} - 4 π^{2} R^{3}}$ B、 $\frac{G T^{2}}{G T^{2} + 4 π^{2} R^{3}}$ C、 $\frac{G T^{2} - 4 π^{2} R^{3}}{G T^{2}}$ D、 $\frac{G T^{2} + 4 π^{2} R^{3}}{G T^{2}}$

查看试题解析
7. 假设有一载人宇宙飞船在距地面高度为4 200 km 的赤道上空绕地球做匀速圆周运动，地球半径约为6 400 km，地球同步卫星距地面高为36 000 km，宇宙飞船和一地球同步卫星绕地球同向运动，每当两者相距最近时，宇宙飞船就向同步卫星发射信号，然后再由同步卫星将信号发送到地面接收站，某时刻两者相距最远，从此刻开始，在一昼夜的时间内，接收站共接收到信号的次数为（　　）

A、4次 B、6次 C、7次 D、8次

查看试题解析

二、多选题

8. 如图所示，一个被无弹性绳子牵引的小球，在光滑水平板上以速度 $v = 2.0 m / s$ 做匀速圆周运动，A轨道运动半径 $r = 30 c m$ 。现迅速松手使绳子放长20cm后立即拽紧绳子，使小球在更大半径的新轨道B上做匀速圆周运动，下列说法正确的是（　　）

A、实现这一过渡所需时间为2.0s B、小球在A轨道和B轨道做匀速圆周运动的线速度之比为5：3 C、小球在A轨道和B轨道做匀速圆周运动的角速度之比为25：9 D、小球在A轨道和B轨道做匀速圆周运动时绳子拉力之比为5：3

查看试题解析
9. 如图所示，飞行器P绕某星球做匀速圆周运动，星球相对飞行器的张角为θ，下列说法正确的是（）

A、轨道半径越大，周期越长 B、轨道半径越大，速度越大 C、若测得周期和张角，可得到星球的平均密度 D、若测得周期和轨道半径，可得到星球的平均密度

查看试题解析
10. 如图所示，水平转盘上沿半径方向放着用细线相连的物体A和B，细线刚好拉直，A和B质量都为m ，它们位于圆心两侧，与圆心距离分别为r、2r ， A、B与盘间的动摩擦因数 $μ$ 相同。若最大静摩擦力等于滑动摩擦力，当圆盘从静止开始缓慢加速到两物体恰要与圆盘发生相对滑动的过程中，下列说法正确的是（　　）

A、绳子的最大张力为 $T = 2 μ m g$ B、A与转盘的摩擦力先增大后减小 C、B与转盘的摩擦力先达到最大静摩擦力且之后保持不变 D、开始转动时两物块均由指向圆心的静摩擦力提供向心力，绳子无拉力

查看试题解析

三、实验题

11. 探究向心力大小 $F$ 与小球质量m、角速度 $ω$ 和半径r之间关系的实验装置如图所示，转动手柄，可使变速塔轮、长槽和短槽随之匀速转动。皮带分别套在塔轮的圆盘上，可使两个槽内的小球分别以不同角速度做匀速圆周运动。小球做圆周运动的向心力由横臂的挡板提供，同时，小球对挡板的弹力使弹簧测力筒下降，从而露出测力筒内的标尺，标尺上露出的红白相间的等分格数之比即为两个小球所受向心力的比值。

(1)、在这个实验中，利用了（选填“理想实验法”“等效替代法”或“控制变量法”）来探究向心力的大小与小球质量m、角速度 $ω$ 和半径r之间的关系；

(2)、探究向心力的大小与圆周运动半径的关系时，应选择两个质量（选填“相同”或“不同”）的小球；

(3)、当用两个质量相等的小球做实验，调整长槽中小球的轨道半径是短槽中小球半径的 $2$ 倍，转动时发现左、右标尺上露出的红白相间的等分格数之比为1：2，则左、右两边塔轮的半径之比为。

查看试题解析
12. 卡文迪许利用如图所示的扭称实验装置测量了引力常量：

(1)、横梁一端固定有一质量为m半径为r的均匀铅球A，旁边有一质量为m，半径为r的相同铅球B，A、B两球表面的最近距离L，已知引力常量为G，则A、B两球间的万有引力大小为F= ．

(2)、在下图所示的几个实验中，与“卡文迪许扭秤实验”中测量微小量的思想方法最相近的是．（选填“甲”“乙”或“丙”）

(3)、引力常量的得出具有重大意义，比如：．（说出一条即可）

查看试题解析

四、解答题

13. 如图所示，长为L的细线，拴一质量为m的小球，细线另一端固定于O点，让小球在水平面内做匀速圆周运动，这种运动通常称为圆锥摆运动。已知运动中细线与竖直方向的夹角为θ，求：

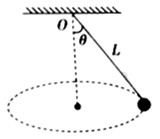(1)、细线对小球拉力F的大小；

(2)、小球运动的周期；

(3)、小球运动的线速度大小。

查看试题解析
14. 宇航员在某星球表面将一小钢球以某一初速度竖直向上抛出，测得小钢球上升的最大高度为h，小钢球从抛出到落回星球表面的时间为t．不计空气阻力，忽略该星球的自转，已知该星球的半径为R（R远大于h），该星球为密度均匀的球体，引力常量为G．求：

(1)、该星球表面的重力加速度；

(2)、该星球的密度；

(3)、该星球的第一宇宙速度。

查看试题解析
15. 有一轨道平面与赤道平面重合的侦察卫星，轨道高度为R ，飞行方向与地球自转方向相同。设地球自转周期为 $T_{0}$ ，半径为R ，地球赤道处的重力加速度为g。位于赤道的某一地面基站在某时刻恰好与该卫星建立起通信链路，求：

(1)、卫星的角速度

(2)、该地面基站能不间断的从侦察卫星上下载侦察数据的时间。

查看试题解析