广东省珠海市2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-08-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案中，可以通过其中一个基础图形平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列实数是无理数的是（）

A、 $- 1$ B、 $\sqrt{6}$ C、 $\sqrt{9}$ D、 $\frac{1}{3}$

查看试题解析
3. 在平面直角坐标系中，下列各点在第四象限的是（）

A、（2，1） B、（2，－1） C、（－2，1） D、（－2，－1）

查看试题解析
4. 下列各式中，属于二元一次方程的是（）

A、 $2 x + 1 = 3$ B、 $x y = 3$ C、 $x - 2 y$ D、 $x = y - 1$

查看试题解析
5. 下列调查案例中，最适宜采用全面调查（普查）方式的是（）

A、调查某市中学生的视力状况 B、检测神舟十六号飞船的零部件 C、调查某河域的水污染情况 D、调查一批节能灯的使用寿命

查看试题解析
6. 如图，直线a、b被直线c所截，下列说法不正确的是（）

A、 $∠ 1$ 和 $∠ 4$ 是同位角 B、 $∠ 2$ 和 $∠ 3$ 是内错角 C、 $∠ 1$ 和 $∠ 2$ 是对顶角 D、 $∠ 3$ 和 $∠ 4$ 是邻补角

查看试题解析
7. 已知 $a < b$ ，下列四个不等式中，正确的是（）

A、 $a - 2 > b - 2$ B、 $a - b > 0$ C、 $2 a < a + b$ D、 $- 2 a < - 2 b$

查看试题解析
8. 用代入法解方程组 ${\begin{array}{l} 2 x - y = 5 ① \\ y = 1 + x ② \end{array}$ 时，把②代入①后得到的方程是（）

A、 $2 x - 1 + x = 5$ B、 $1 + x = 2 x + 5$ C、 $5 - 2 x = 1 + x$ D、 $2 x - 1 - x = 5$

查看试题解析
9. 2023年2月26日，横琴马拉松在广东珠海横琴金融岛中央公园开跑．小强跑在小海前面，在离终点 $1000 m$ 时，他以 $5 m / s$ 的速度向终点冲刺，而此时小海在他身后 $100 m$ ，请问小海需以多快的速度同时冲刺，才能在小强之前到达终点？设此时小海冲刺的速度为 $x m / s$ ，可列的不等式为（）

A、 $\frac{1000 + 100}{5} x > 1000$ B、 $\frac{1000}{5} x > 1000 + 100$ C、 $\frac{1000 + 100}{5} x < 1000$ D、 $\frac{1000}{5} x < 1000 + 100$

查看试题解析
10. 如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“1”，若 $B C ⊥ E F$ ， $∠ A B C = 140 °$ ， $∠ A F E = 75 °$ ，则 $∠ A$ 的度数为（）

A、 $40 °$ B、 $30 °$ C、 $25 °$ D、 $20 °$

查看试题解析

二、填空题

11. 已知 $x + y = 3$ ，当 $x = 2$ 时， $y =$ ．

查看试题解析
12. 一个正数的平方根是m与 $m - 4$ ，则 $m =$ ．

查看试题解析
13. 如图，直线 $A B$ 与直线 $C D$ 相交于点 $O$ ，若 $∠ B O E = 35 °$ ， $E O ⊥ C D$ ，垂足为 $O$ ，则 $∠ A O C =$ 度．

查看试题解析
14. 在五子棋比赛中，黑白双方轮流落子，率先在横、竖、斜任一方向上成连续五枚同色棋子的一方为胜．如图，现黑方有一个方向形成了同色“四连珠”，已锁定胜局，黑方下一步终结棋局的落子位置的坐标是．

查看试题解析
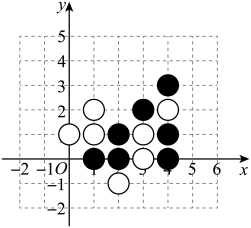15. 下表中给出的每一对x ， y的值都是二元一次方程 $a x + b y = 3$ 的解，则不等式组 ${\begin{array}{l} x < m \\ x > n \end{array}$ 的解集为．

$x$

$m$

1

2

3

$y$

3

1

$- 1$

$n$

查看试题解析

三、解答题

16. 计算： $\sqrt{4} - \sqrt[3]{27} + | 1 - \sqrt{3} |$ ．

查看试题解析
17. 解不等式组 ${\begin{array}{l} 1 - x \leq 2 \\ \frac{x + 1}{2} < 1 \end{array}$ 并写出所有整数解．

查看试题解析
18. 三角形 $A B C$ 的三个顶点均在如图所示的正方形网格中的格点上，每个小正方形的边长是1个单位，已知A ， C两点在平面直角坐标系中的坐标为 $A (2 ， 0)$ ， $C (- 1 ， 2)$ ．

(1)、请在图中建立正确的平面直角坐标系，并写出点B的坐标；

(2)、现将三角形 $A B C$ 平移，使得点C移至图中的点 $C^{'}$ 的位置，请画出平移后的三角形 $A^{'} B^{'} C^{'}$ ．

查看试题解析
19. 2023年4月15日是第八个全民国家安全教育日，主题是“贯彻总体国家安全观，增强全民国家安全意识和素养，夯实以新安全格局保障新发展格局的社会基础”某中学为了调查学生对国家安全相关知识的掌握情况，随机抽取若干学生进行了相关知识测试，将成绩（取整数）分为“ $A$ ： $90 ∼ 100$ 分， $B$ ： $80 \sim 89$ 分， $C$ ： $70 \sim 79$ 分， $D$ ： $69$ 分及以下”四个等级进行统计，绘成如图所示的不完整统计图．解答下列问题：

(1)、此次测试被抽取的学生共人．扇形统计图中， $A$ 等级对应扇形的圆心角度数为；

(2)、请补全条形统计图；

(3)、若该校 $800$ 名学生都参加此次测试，将对 $80$ 分以上（含 $80$ 分）进行表彰，估计该校被表彰的学生有多少人？

查看试题解析
20. 如图，已知 $∠ A B C = ∠ C$ ， $∠ A = ∠ E$ ．

(1)、求证： $A D ∥ B E$ ；

(2)、若 $∠ 1 = ∠ 2 = 69 °$ ， $∠ D B E = 2 ∠ C B D$ ，求 $∠ A$ 的度数．

查看试题解析

21. 5月至10月，广东省居民阶梯电价实行“夏季模式”，具体收费标准如下表：

档次	用电量（度）	单价（元/度）
第一档	不超过260	x
第二档	超过260，不超过600的部分	y
第三档	超过600的部分	0.9

小海家2021年7月、8月用电量分别是560度和760度，缴纳电费分别为351元和521元．

(1)、求表中的x和y的值；

(2)、广东省自2021年6月1日起执行居民阶梯电价“一户多人口”政策，如果一户家庭人口满5人及以上可申请每户每月第一、二、三档分别增加100度阶梯电量基数．小海家庭人口为6人，若申请“一户多人口”政策，小海家2021年7、8月份共可省多少电费？

查看试题解析

22. 阅读下面一段材料，并解答材料后的问题：
我们知道 $π$ 是无理数，而无理数是无限不循环小数，为表示出其小数部分，可以这样考虑： $∵ 3 < π < 4$ ， $∴ π$ 的整数部分为3，小数部分为 $π - 3$ ．再如： $∵ \sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ， $∴ \sqrt{7}$ 的整数部分为2，小数部分为 $\sqrt{7} - 2$ ．

(1)、若 $\sqrt{19}$ 的整数部分为m ，小数部分为n ，则 $m =$ ， $n =$ ；

(2)、已知 $x + y = 10 + \sqrt{3}$ ．
①若x是整数，且 $0 < y < 1$ ，求 $x - 2 y$ 的值；

②若x ， y分别是一张长方形纸片 $A B C D$ 的长和宽，将该纸片按如下图方式先折一下，然后剪开，可以得到一个正方形 $A B F E$ 和一个长方形 $C D E F$ ，已知 $C D = 2 D E$ ．求证： $4 < y < 5$ ．

查看试题解析
23. 如图，在平面直角坐标系中，直线l与x轴相交于点P ，直线l上的两点 $A (1 ， a)$ ， $B (b ， 1)$ 满足 $\sqrt{a - 3} + | b + 1 | = 0$ ，将线段 $A B$ 向右平移5个单位长度得到线段 $D C$ ．

(1)、点C的坐标为；

(2)、连接 $A D$ ， $B C$ ， $A C$ ，点Q是x轴上一点（不与点P重合），连接 $A Q$ ，交 $B C$ 于点E ．
①当 $A C$ 恰好平分 $∠ D A Q$ 时，试判断 $∠ A Q P$ 与 $∠ A C B$ 有什么数量关系？并说明理由；

②设点 $Q (t ， 0)$ ，记三角形 $A B Q$ 的面积为S ，三角形 $A O C$ 的面积为 $S_{0}$ ．当 $S = \frac{8}{11} S_{0}$ 时，求点Q的坐标．

查看试题解析

$x$	$m$	1	2	3
$y$	3	1	$- 1$	$n$