湖北省黄冈市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-08-07 类型：期末考试

进入出卷网下载

一、选择题（本题共8小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的，不涂、错涂或涂的代号超过一个，一律得0分）

1. 若二次根式 $\sqrt{x - 1}$ 有意义，则x的取值范围为（）

A、 $x \neq 1$ B、全体实数 C、 $x < 1$ D、 $x \geq 1$

查看试题解析
2. 若平行四边形中两个内角的度数比为1：4，则其中较小的内角是（）

A、36° B、40° C、45° D、48°

查看试题解析
3. 毓秀中学举行演讲比赛活动，共有15人参加演讲比赛，参赛选手的成绩各不相同，因此选手要想知道自己是否进入前八名，只需了解自己的成绩以及全部成绩的（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
4. 正比例函数 $y = k x (k \neq 0)$ 的图象经过点（1，－2），则正比例函数的解析式为（）

A、y＝2x B、 $y = \frac{1}{2} x$ C、y＝－2x D、 $y = - \frac{1}{2} x$

查看试题解析
5. 由线段a，b，c组成的三角形是直角三角形的是（）

A、a＝2，b＝3，c＝4 B、 $a = \sqrt{2}$ ， $b = \sqrt{3}$ ， $c = \sqrt{5}$ C、a＝40，b＝50，c＝60 D、 $a = \frac{1}{3}$ ， $b = \frac{1}{4}$ ， $c = \frac{1}{5}$

查看试题解析
6. 若点（m，n）在函数y＝2x＋1的图象上，则2m－n的值是（）

A、－1 B、1 C、±1 D、 $\frac{1}{2}$

查看试题解析
7. 下列说法中，正确的是（）
①两条对角线互相平分的四边形是平行四边形；
②两条对角线相等的四边形是矩形；
③两条对角线互相垂直的平行四边形是菱形；
④两条对角线相等的菱形是正方形．

A、①②③ B、①③④ C、①② D、①②③④

查看试题解析
8. 甲、乙两车分别从A，B两地同时出发，沿同一条公路相向而行，相遇时甲、乙所行驶路程的比为2：3，甲、乙两车离AB中点M路程y（千米）与甲车出发时间x（时）的关系图象如图所示，则下列说法中正确结论的个数有（）
①乙车的速度为90千米/时；②a的值为 $\frac{5}{2}$ ；③b的值为150；④当甲、乙两车相距30千米时，甲行走了 $\frac{9}{5}$ 小时或 $\frac{11}{5}$ 小时．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分．请将结果直接写在答题卡上相应位置上）

9. 若 $a$ <0，化简 $| a - 3 | - \sqrt{a^{2}} =$ .

查看试题解析
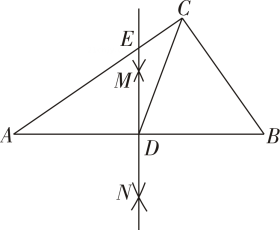
10. 如图，在 $R t △ A B C$ 中，∠ACB＝90°，通过尺规作图得到的直线MN分别交AB，AC于点D，E，连接CD．若 $C E = \frac{1}{3} A E = 1$ ，则CD＝．

查看试题解析

11. 生物学研究表明，植物光合作用速率越高，单位时间内合成的有机物越多．为了解甲、乙两个品种大豆的光合作用速率，科研人员从甲、乙两个品种的大豆中各选五株，在同等实验条件下，测量它们的光合作用速率（单位：

μ m o l \cdot m^{- 2} \cdot s^{- 1}

），结果统计如下：

品种	第一株	第二株	第三株	第四株	第五株	平均数
甲	32	30	25	18	20	25
乙	28	25	26	24	22	25

则两个大豆品种中光合作用速率更稳定的是（填“甲”或“乙”）．

查看试题解析

12. 两直线 $l_{1}$ ：y＝2x－1与 $l_{2}$ ：y＝x＋1的交点坐标为．

查看试题解析
13. 如图，菱形 $A B C D$ 的对角线 $A C ， B D$ 相交于点O，点E在 $O B$ 上，连接 $A E$ ，点F为 $C D$ 的中点，连接 $O F$ ，若 $A E = B E$ ， $O E = 3$ ， $O A = 4$ ，则线段 $O F$ 的长为．

查看试题解析
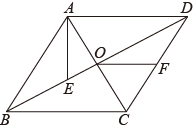14. 如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，那么小鸟飞行的距离至少为米．

查看试题解析
15. 如图，直线y＝2x＋4与x轴交于点A，与y轴交于点B，点D为OB的中点， $▱ O C D E$ 的顶点C在x轴上，顶点E在直线AB上，则 $▱ O C D E$ 的面积为．

查看试题解析
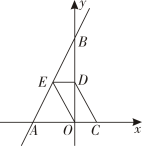16. 如图（1），在矩形ABCD中，动点P从点B出发，沿BC—CD—DA运动至点A停止．点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图（2）所示，则面积y的最大值是．

查看试题解析

三、解答题（本大题共8小题，满分72分．解答写在答题卡上）

17. 计算：

(1)、 $\frac{\sqrt{20} + \sqrt{5}}{\sqrt{5}} - 2$ ；

(2)、 $(\sqrt{48} - \sqrt{3}) \times \sqrt{3} - \sqrt{4}$ ．

查看试题解析
18. 如图，在四边形ABCD中，对角线AC和BD相交于点O，AO＝CO，∠BCA＝∠CAD．求证：四边形ABCD是平行四边形．

查看试题解析
19. 已知一次函数y＝kx－4，当x＝2时，y＝－3．

(1)、求一次函数的解析式；

(2)、将该函数的图象向上平移6个单位，求平移后的图象与x轴交点的坐标．

查看试题解析

20. 某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分满分均为100分．第1~6号选手的得分如下：

序号项目	1	2	3	4	5	6
笔试成绩（分）	85	92	84	90	84	80
面试成绩（分）	90	88	86	90	80	85

根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩（综合成绩的满分仍为100分）．

(1)、这6名选手笔试成绩的中位数是分，众数是分．

(2)、现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比．

(3)、求出其余5名选手的综合成绩，并以综合成绩由高到低排序，确定前两名人选．

查看试题解析

21. 如图，每个小正方形的边长为1，四边形ABCD的每个顶点都在网格的格点上，且 $A B = \sqrt{26}$ ， $A D = \sqrt{17}$ ．

(1)、请在图中标出点A位置，补全四边形ABCD，并求其面积；

(2)、判断∠BCD是直角吗？请说明理由．

查看试题解析
22. 为了振兴乡村经济，我市某镇鼓励广大农户种植山药，并精加工成甲、乙两种产品．某经销商购进甲、乙两种产品，甲种产品进价为8元/kg；乙种产品的进货总金额y（单位：元）与乙种产品进货量x（单位：kg）之间的关系如图所示．已知甲、乙两种产品的售价分别为12元/kg和18元/kg．

(1)、求出 $0 \leq x \leq 2000$ 和 $x > 2000$ 时，y与x之间的函数关系式；

(2)、若该经销商购进甲、乙两种产品共6000kg，并能全部售出．其中乙种产品的进货量不低于1600kg，且不高于4000kg，设销售完甲、乙两种产品所获总利润为w元（利润＝销售额－成本），请求出w（单位：元）与乙种产品进货量x（单位：kg）之间的函数关系式，并为该经销商设计出获得最大利润的进货方案．

查看试题解析
23. 如图，已知直线AB的函数解析式为y＝2x＋10，与y轴交于点A，与x轴交于点B．

(1)、求A、B两点的坐标；

(2)、若点P（a，b）为线段AB上的一个动点，作PE⊥y轴于点E，PF⊥x轴于点F，连接EF，问：
①若四边形PBOE的面积为S，求S关于a的函数关系式；
②是否存在点P，使线段EF的值最小？若存在，求出EF的最小值；若不存在，请说明理由．

查看试题解析
24. 同学们还记得吗？图①，图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形．受这两个图形的启发，数学兴趣小组提出了以下三个问题，请你回答：

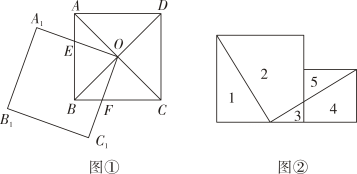
(1)、【问题一】
如图①，正方形ABCD的对角线相交于点O，点O又是正方形 $A_{1} B_{1} C_{1} O$ 的一个顶点， $O A_{1}$ 交AB于点E， $O C_{1}$ 交BC于点F，则AE与BF的数量关系为；

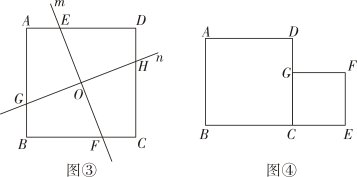
(2)、【问题二】
受图①启发，兴趣小组画出了图③：直线m、n都经过正方形ABCD的对角线交点O，直线m分别与AD、BC交于点E、F，直线n分别与AB、CD交于点G、H，且m⊥n，若正方形ABCD边长为8，求四边形OEAG的面积；

(3)、【问题三】
受图②启发，兴趣小组画出了图④：正方形CEFG的顶点G在正方形ABCD的边CD上，顶点E在BC的延长线上，且BC＝6，CE＝2．在直线BE上是否存在点P，使得△APF为直角三角形？若存在，求出BP的长度；若不存在，说明理由．

查看试题解析