2023年浙教版数学九年级上册第三章 圆的基本性质 章末检测(B卷)
试卷更新日期:2023-08-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,已知OA,OB, OC是⊙O的半径,连结BC,交OA于点D,设∠ADB=a,∠OBC=p,∠AOC=y, 则( )
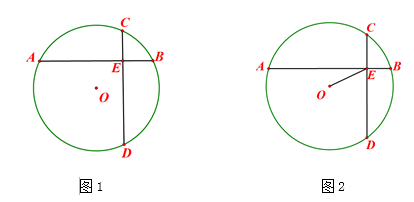
 A、a+2β-y= 180° B、a+β+y= 180° C、2a-β+y=180° D、3a-2β+y=180°2. 如图,在中, , , , 点D在边上, , 以点D为圆心作 , 其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )
A、a+2β-y= 180° B、a+β+y= 180° C、2a-β+y=180° D、3a-2β+y=180°2. 如图,在中, , , , 点D在边上, , 以点D为圆心作 , 其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )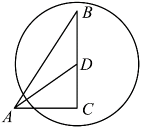 A、 B、 C、 D、3. 如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得 , 若点在AB上,则的长为( )
A、 B、 C、 D、3. 如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得 , 若点在AB上,则的长为( )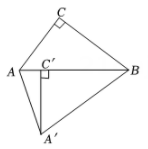 A、 B、4 C、 D、54. 木条 、 、 如图用螺丝固定在木板 上在且 ,将木条 、木条 、木条 看作是在同一平面 内的三条直线 、 、 ,若使直线 、直线 达到平行的位置关系则下列描述错误的是( )
A、 B、4 C、 D、54. 木条 、 、 如图用螺丝固定在木板 上在且 ,将木条 、木条 、木条 看作是在同一平面 内的三条直线 、 、 ,若使直线 、直线 达到平行的位置关系则下列描述错误的是( )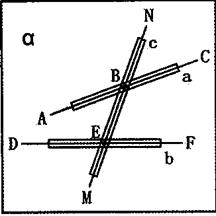 A、木条 、 固定不动,木条 绕点B顺时针旋转 B、木条 、 固定不动,木条 绕点 逆时针旋转 C、木条 、 固定不动,木条 绕点 逆时针旋转 D、木条 、 固定不动,木条 绕点 顺时针旋转5. 如图,四边形为矩形,AB = 3,BC = 4.点P是线段上一动点,点M为线段AP上一点. , 则的最小值为( )
A、木条 、 固定不动,木条 绕点B顺时针旋转 B、木条 、 固定不动,木条 绕点 逆时针旋转 C、木条 、 固定不动,木条 绕点 逆时针旋转 D、木条 、 固定不动,木条 绕点 顺时针旋转5. 如图,四边形为矩形,AB = 3,BC = 4.点P是线段上一动点,点M为线段AP上一点. , 则的最小值为( )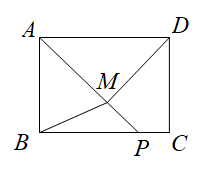 A、 B、 C、 D、6. 如图,AB是⊙O的一条弦, , =120°,点D在⊙O上,CD⊥AB于点C,BC-AC=12,则CD的长为( )
A、 B、 C、 D、6. 如图,AB是⊙O的一条弦, , =120°,点D在⊙O上,CD⊥AB于点C,BC-AC=12,则CD的长为( )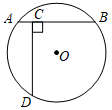 A、 B、 C、13 D、127. 如图,是的内接三角形,是的直径,若则 ( )
A、 B、 C、13 D、127. 如图,是的内接三角形,是的直径,若则 ( )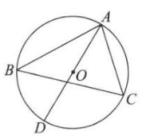 A、 B、 C、 D、8. 如图,A、B,C是⊙O上的点,且∠ACB=140°.在这个图中,画出下列度数的圆周角:40°,50°,90°,140°,仅用无刻度的直尺能画出的有( )
A、 B、 C、 D、8. 如图,A、B,C是⊙O上的点,且∠ACB=140°.在这个图中,画出下列度数的圆周角:40°,50°,90°,140°,仅用无刻度的直尺能画出的有( )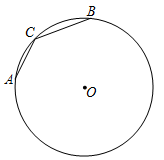 A、1个 B、2个 C、3个 D、4个9. 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥边BC于点M,若⊙O的半径为4,则边心距OM的长为( )
A、1个 B、2个 C、3个 D、4个9. 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥边BC于点M,若⊙O的半径为4,则边心距OM的长为( )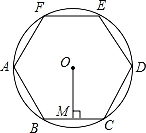 A、2 B、 C、2 D、210. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )
A、2 B、 C、2 D、210. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )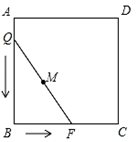 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
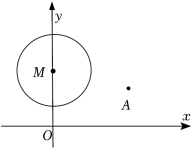
11. 如图,平面直角坐标系中有一点 ,在以 为圆心,2为半径的圆上有一点P,将点P绕点A旋转 后恰好落在x轴上,则点P的坐标是.
 12. 如图,为的直径,弦 , 垂足为 , , , , 则弦的长度为.
12. 如图,为的直径,弦 , 垂足为 , , , , 则弦的长度为. 13. 如图所示, 是 的直径, , ,则 的度数为 .
13. 如图所示, 是 的直径, , ,则 的度数为 .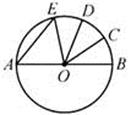 14. 如图,在正方形ABCD中,AB=2 , 将线段CD绕点C顺时针旋转α至射线l,作点D关于射线l的对称点M,连接BM交直线l于点N,当α=°时,线段AN取得最大值;线段AN的最大值为.
14. 如图,在正方形ABCD中,AB=2 , 将线段CD绕点C顺时针旋转α至射线l,作点D关于射线l的对称点M,连接BM交直线l于点N,当α=°时,线段AN取得最大值;线段AN的最大值为. 15. 如图,点A,B,C,D,E都是⊙O上的点,AC=AE,∠D=128°,则∠B=°。
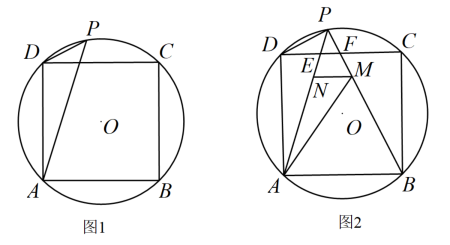
15. 如图,点A,B,C,D,E都是⊙O上的点,AC=AE,∠D=128°,则∠B=°。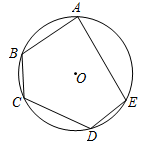 16. 如图,正方形 和正 都内接于半径为1的 , 与 、 分别相交于点 、 ,则 的长为.
16. 如图,正方形 和正 都内接于半径为1的 , 与 、 分别相交于点 、 ,则 的长为.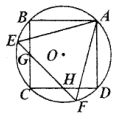
三、解答题(共9题,共72分)
-
17. 如图,在平面直角坐标系中,点 , 点 , 点.
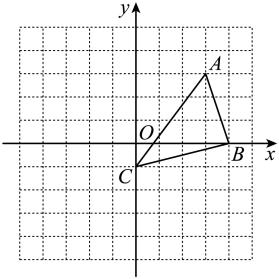 (1)、以点为中心,把逆时针旋转 , 画出旋转后的图形;(2)、在(1)中的条件下,
(1)、以点为中心,把逆时针旋转 , 画出旋转后的图形;(2)、在(1)中的条件下,①扫过的面积为(结果保留);
②写出点的坐标为.
18. 如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.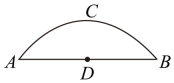 (1)、求拱桥的半径.(2)、有一艘宽为7.8m的货船,船舱顶部为长方形,并高出水面3m,则此货船是否能顺利通过此圆弧形拱桥?并说明理由.19.
(1)、求拱桥的半径.(2)、有一艘宽为7.8m的货船,船舱顶部为长方形,并高出水面3m,则此货船是否能顺利通过此圆弧形拱桥?并说明理由.19.如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
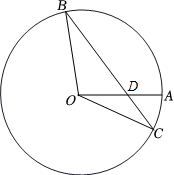
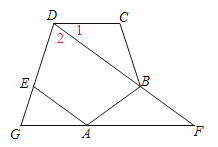 (1)、写出图中所有的等腰三角形;(2)、求证:∠G=2∠F.20. 如图,已知 是 的外接圆,点D是 上的一个动点,且C , D位于 的两侧,联结 , ,过点C作 ,垂足为E.延长 交 于点F , , 的延长线交于点P.
(1)、写出图中所有的等腰三角形;(2)、求证:∠G=2∠F.20. 如图,已知 是 的外接圆,点D是 上的一个动点,且C , D位于 的两侧,联结 , ,过点C作 ,垂足为E.延长 交 于点F , , 的延长线交于点P.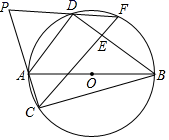
求证:
(1)、 .(2)、 是等腰三角形.21. 已知:如图,内接于 , 为直径,的平分线交于点 , 交于点 , 于点 , 且交于点 , 连接.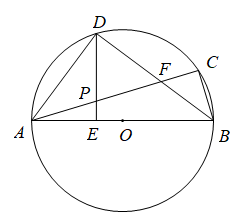 (1)、求证:;(2)、连接 , 若 , , 求的半径和的长.22. 如图,在平面直角坐标系中,有Rt△ABC,∠ACB=90°,∠BAC=30°,点A、B均在x轴上,边AC与y轴交于点D,连结BD,点B的坐标为( ,0),若BD是∠ABC的角平分线.
(1)、求证:;(2)、连接 , 若 , , 求的半径和的长.22. 如图,在平面直角坐标系中,有Rt△ABC,∠ACB=90°,∠BAC=30°,点A、B均在x轴上,边AC与y轴交于点D,连结BD,点B的坐标为( ,0),若BD是∠ABC的角平分线. (1)、如图1,求点C的坐标;(2)、如图2,将Rt△ABC绕点A逆时针旋转一个角度α(0°≤α≤180°)得到Rt△AB'C',直线AC'交直线BD于点P,直线AB'交y轴于点Q,是否存在点P、Q,使△APQ为等腰三角形?若存在,直接写出∠APQ的度数;若不存在,请说明理由.23. 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,∠EAC=120°.
(1)、如图1,求点C的坐标;(2)、如图2,将Rt△ABC绕点A逆时针旋转一个角度α(0°≤α≤180°)得到Rt△AB'C',直线AC'交直线BD于点P,直线AB'交y轴于点Q,是否存在点P、Q,使△APQ为等腰三角形?若存在,直接写出∠APQ的度数;若不存在,请说明理由.23. 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,∠EAC=120°. (1)、连OB,OC,求∠OCB;(2)、连DB,DC,求证:DB=DC;(3)、探究线段AD,AB,AC之间的数量关系,并证明你的结论.
(1)、连OB,OC,求∠OCB;(2)、连DB,DC,求证:DB=DC;(3)、探究线段AD,AB,AC之间的数量关系,并证明你的结论.