2023年浙教版数学九年级上册第三章 圆的基本性质 章末检测(A卷)
试卷更新日期:2023-08-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列图形为圆的是( )A、
 B、
B、  C、
C、  D、
D、 2. 点到圆的距离为6,若点在圆外,则圆的半径满足( )A、 B、 C、 D、3. 的外心在三角形的内部,则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法判断4. 下列各图中,能通过一个三角形绕一点旋转一次得到另一三角形的图形是( )A、
2. 点到圆的距离为6,若点在圆外,则圆的半径满足( )A、 B、 C、 D、3. 的外心在三角形的内部,则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法判断4. 下列各图中,能通过一个三角形绕一点旋转一次得到另一三角形的图形是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,⊙O的直径CD垂直弦AB于点E,且CE=2, DE=8,则AB的长为( )
5. 如图,⊙O的直径CD垂直弦AB于点E,且CE=2, DE=8,则AB的长为( ) A、4 B、6 C、7 D、86. 下列语句中,正确的有( )
A、4 B、6 C、7 D、86. 下列语句中,正确的有( )相等的圆心角所对的弧相等;等弦对等弧;平分弦的直径垂直于弦;经过圆心的每一条直线都是圆的对称轴.
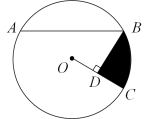
A、1个 B、2个 C、3个 D、4个7. 如图,在中,是直径,是弦若 , 则( )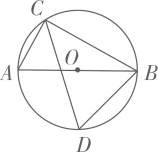 A、 B、 C、 D、8. 如图,已知圆心角 , 则圆周角( )
A、 B、 C、 D、8. 如图,已知圆心角 , 则圆周角( ) A、 B、 C、 D、9. 若正六边形的周长为24,则它的外接圆的半径为( )A、4 B、4 C、2 D、210. 若扇形的半径是弧长是 , 则扇形的面积为( )A、 B、 C、 D、
A、 B、 C、 D、9. 若正六边形的周长为24,则它的外接圆的半径为( )A、4 B、4 C、2 D、210. 若扇形的半径是弧长是 , 则扇形的面积为( )A、 B、 C、 D、二、填空题(每空4分,共24分)
-
11. 平面上不共线的四点,可以确定圆的个数为 .12. 如图,把△ABC绕B点逆时针方向旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC= .
 13. 五水共治办公室在一次巡查时测量一排水管的排水情况,如图,水平放置的圆柱形排水管的截面为 , 半径是 , 有水部分弓形的高为 , 则.
13. 五水共治办公室在一次巡查时测量一排水管的排水情况,如图,水平放置的圆柱形排水管的截面为 , 半径是 , 有水部分弓形的高为 , 则. 14. 如图,在⊙O中, , AD⊥OC于点D,比较大小AB2AD.(填入“>”或“<”或“=”).
14. 如图,在⊙O中, , AD⊥OC于点D,比较大小AB2AD.(填入“>”或“<”或“=”). 15. 已知四边形内接于 , 若 , 则的度数为.16. 若扇形的圆心角为 , 半径为 , 则扇形的弧长为.
15. 已知四边形内接于 , 若 , 则的度数为.16. 若扇形的圆心角为 , 半径为 , 则扇形的弧长为.三、作图题(共8分)
-
17. 如图,在6×6的方格中,有一格点△ABC(顶点都在小正方形的顶点上)及格点P,按下列要求画格点三角形.
 (1)、在图1中,画出△ABC绕点P顺时针旋转90°后的三角形△A'B'C'.(2)、在图2中,画出△ABC绕某一点顺时针旋转90°后的△DEF,且点P在△DEF内(不包括边界).
(1)、在图1中,画出△ABC绕点P顺时针旋转90°后的三角形△A'B'C'.(2)、在图2中,画出△ABC绕某一点顺时针旋转90°后的△DEF,且点P在△DEF内(不包括边界).四、解答题(共7题,共58分)
-
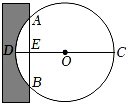
18. 《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
 19. 如图AB,CD为⊙O内两条相交的弦,AD=BC,求证:AB=CD
19. 如图AB,CD为⊙O内两条相交的弦,AD=BC,求证:AB=CD 20. 如图,⊙O中,弦AB与CD相交于点H,AB=CD,连接AD、BC.求证:AH=CH.
20. 如图,⊙O中,弦AB与CD相交于点H,AB=CD,连接AD、BC.求证:AH=CH. 21. 已知四边形ABCD内接于⊙O,= , ∠ADC=120°,求证:△ABC是等边三角形.
21. 已知四边形ABCD内接于⊙O,= , ∠ADC=120°,求证:△ABC是等边三角形.
-