2023年浙教版数学九年级上册3.6 圆内四边形 同步测试(提高版)
试卷更新日期:2023-08-06 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在中,点A、B、C在圆上,点D在AB的延长线上,已知 , 则( )
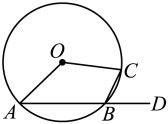 A、 B、 C、 D、2. 如图,在中,.是的外接圆,为弧的中点,为延长线上一点.若 , 则的度数是( )
A、 B、 C、 D、2. 如图,在中,.是的外接圆,为弧的中点,为延长线上一点.若 , 则的度数是( )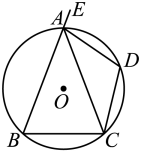 A、 B、 C、 D、3. 如图,在中,点是上一点,若 , 则的度数为( )
A、 B、 C、 D、3. 如图,在中,点是上一点,若 , 则的度数为( ) A、 B、 C、 D、4. 如图,已知圆心角∠AOB=140°,则圆周角∠ACB=( )
A、 B、 C、 D、4. 如图,已知圆心角∠AOB=140°,则圆周角∠ACB=( ) A、40° B、70° C、110° D、120°5. 如图,四边形内接于 , , , , 点为的中点,则线段的长为( )
A、40° B、70° C、110° D、120°5. 如图,四边形内接于 , , , , 点为的中点,则线段的长为( )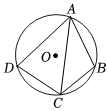 A、 B、 C、 D、6. 如图,AB是半圆O的直径,点D是弧AC的中点,若∠BAC=44°,则∠DAC等于( )
A、 B、 C、 D、6. 如图,AB是半圆O的直径,点D是弧AC的中点,若∠BAC=44°,则∠DAC等于( )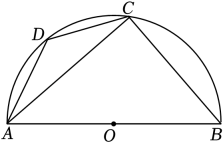 A、22° B、44° C、23° D、46°7. 如图,点、、在上, , , 则的度数是 ( )
A、22° B、44° C、23° D、46°7. 如图,点、、在上, , , 则的度数是 ( )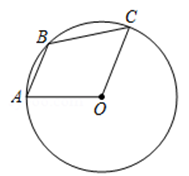 A、 B、 C、 D、8. 如图,点、、、、都是上的点, , , 则的度数为( )
A、 B、 C、 D、8. 如图,点、、、、都是上的点, , , 则的度数为( ) A、 B、 C、 D、9. 如图,四边形ABCD内接于⊙O,已知点C为的中点,若∠A=50°,则∠CBD的度数为( )
A、 B、 C、 D、9. 如图,四边形ABCD内接于⊙O,已知点C为的中点,若∠A=50°,则∠CBD的度数为( ) A、50° B、40° C、30° D、25°10. 如图,四边形ABCD内接于⊙O,点I是△ABC的角平分线的交点,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A、50° B、40° C、30° D、25°10. 如图,四边形ABCD内接于⊙O,点I是△ABC的角平分线的交点,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( ) A、56 ° B、62° C、68° D、78°
A、56 ° B、62° C、68° D、78°二、填空题(每空4分,共24分)
-
11. 如图,四边形的顶点、、在上,若 , 则.
 12. 如图,在中,是的中点,作点关于弦的对称点 , 连接并延长交于点 , 过点作于点 , 若 , 则等于度.
12. 如图,在中,是的中点,作点关于弦的对称点 , 连接并延长交于点 , 过点作于点 , 若 , 则等于度. 13. 如图,在扇形中,点C、D在上,连接、交于点E,若 , 的度数为 , 则°.
13. 如图,在扇形中,点C、D在上,连接、交于点E,若 , 的度数为 , 则°. 14. 在等边中,以边的中点O为圆心,长为半径画圆,分别交边,于点D,E;P是圆上一动点(与点D、E不重合),连接 , 则.15. 如图,在⊙O中,直径 , 则弦AC所对圆周角为.
14. 在等边中,以边的中点O为圆心,长为半径画圆,分别交边,于点D,E;P是圆上一动点(与点D、E不重合),连接 , 则.15. 如图,在⊙O中,直径 , 则弦AC所对圆周角为. 16. 半径为的圆中有一条弦长为的弦,那么这条弦所对的圆周角的度数等于.
16. 半径为的圆中有一条弦长为的弦,那么这条弦所对的圆周角的度数等于.三、解答题(共8题,共66分)
-
17. 如图,四边形内接于 , 分别延长 , , 使它们相交于点 , , 且.
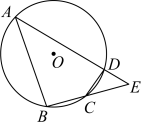 (1)、求证:.(2)、若 , 点为的中点,求的半径.18. 如图,圆中延长弦 , 交于点 , 连接 , , , .
(1)、求证:.(2)、若 , 点为的中点,求的半径.18. 如图,圆中延长弦 , 交于点 , 连接 , , , . (1)、若 , , 求的度数;(2)、若 , , , 判断 , , 满足什么数量关系时,?请说明理由.19. 如图,在△ABC中,AB=AC,以AB为直径的半圆O分别交BC,AC于点D,E,连接DE,OD.
(1)、若 , , 求的度数;(2)、若 , , , 判断 , , 满足什么数量关系时,?请说明理由.19. 如图,在△ABC中,AB=AC,以AB为直径的半圆O分别交BC,AC于点D,E,连接DE,OD. (1)、求证: .(2)、当 , 的度数之比为4∶5时,求四边形ABDE四个内角的度数.20. 如图,四边形是的内接四边形, , 点是的中点.
(1)、求证: .(2)、当 , 的度数之比为4∶5时,求四边形ABDE四个内角的度数.20. 如图,四边形是的内接四边形, , 点是的中点.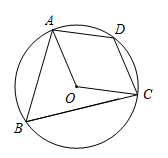 (1)、求的度数;(2)、求证:四边形是菱形.21. 如图,在平面直角坐标系中,O为原点,A(3,0),B(-3,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列),BC与经过A、B、D三点的OM交于点E,DE平分∠ADC,连结AE,BD。
(1)、求的度数;(2)、求证:四边形是菱形.21. 如图,在平面直角坐标系中,O为原点,A(3,0),B(-3,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列),BC与经过A、B、D三点的OM交于点E,DE平分∠ADC,连结AE,BD。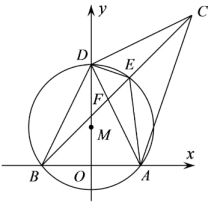 (1)、求证:∠ABC=45°;(2)、求证:∠DEC=DEA;(3)、若点D的坐标为(0,9),求AE的长.22. 如图,在半径为6的扇形中, , C是上的一个动点(不与A,B重合), , 垂足分别为点D,E.
(1)、求证:∠ABC=45°;(2)、求证:∠DEC=DEA;(3)、若点D的坐标为(0,9),求AE的长.22. 如图,在半径为6的扇形中, , C是上的一个动点(不与A,B重合), , 垂足分别为点D,E. (1)、求的长.(2)、求四边形各内角的度数.23. 已知钝角三角形内接于分别为的中点,连接.
(1)、求的长.(2)、求四边形各内角的度数.23. 已知钝角三角形内接于分别为的中点,连接. (1)、如图1,当点在同一条直线上时,求证:.(2)、如图2,当不在同一条直线上时,取的中点 , 连接交于点 , 当时.
(1)、如图1,当点在同一条直线上时,求证:.(2)、如图2,当不在同一条直线上时,取的中点 , 连接交于点 , 当时.①求证:是等腰三角形;
②如图3,连并延长交于点 , 连接.求证:.
24. 定义:若两个三角形中,有两组边对应相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏等三角形.(1)、如图1,点是弧的中点,是弧所对的圆周角, 连接、 试说明与是偏等三角形. (2)、如图2,与是偏等三角形,其中 猜想结论:一对偏等三角形中,一组等边的对角相等,另一组等边的对角 . 请填写结论,并说明理由.(以与为例说明);
(2)、如图2,与是偏等三角形,其中 猜想结论:一对偏等三角形中,一组等边的对角相等,另一组等边的对角 . 请填写结论,并说明理由.(以与为例说明); (3)、如图3,内接于 若点在上,且与是偏等三角形, 求的值.
(3)、如图3,内接于 若点在上,且与是偏等三角形, 求的值.