2023年浙教版数学九年级上册3.6 圆内四边形 同步测试(培优版)
试卷更新日期:2023-08-06 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 在中,弦垂直平分半径 , 点在上(不与点 , 重合),则的度数为( )A、 B、 C、或 D、或2. 如图,四边形是的内接四边形, , 则的度数为( )
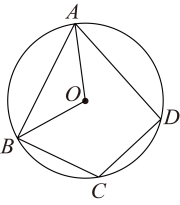 A、 B、 C、 D、3. 如图,在圆内接四边形中, , 为直径,若四边形的面积是S,的长是x,则S与x之间的数关系式是( )
A、 B、 C、 D、3. 如图,在圆内接四边形中, , 为直径,若四边形的面积是S,的长是x,则S与x之间的数关系式是( ) A、 B、 C、 D、4. 如图,四边形是的内接四边形,点是的中点,点是上的一点,若 , 则的度数是( )
A、 B、 C、 D、4. 如图,四边形是的内接四边形,点是的中点,点是上的一点,若 , 则的度数是( ) A、 B、 C、 D、5. 如图,是半圆O的直径,C、D、E三点依次在半圆O上,若 , , 则与之间的关系是( )
A、 B、 C、 D、5. 如图,是半圆O的直径,C、D、E三点依次在半圆O上,若 , , 则与之间的关系是( ) A、 B、 C、 D、6. 如图,四边形为正方形,其中分别以为直径在正方形内部做半圆,正方形的对角线交于O点,点E是以为直径的半圆上的一个动点,则下列结论错误的是( )
A、 B、 C、 D、6. 如图,四边形为正方形,其中分别以为直径在正方形内部做半圆,正方形的对角线交于O点,点E是以为直径的半圆上的一个动点,则下列结论错误的是( )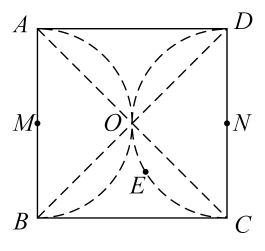 A、若正方形的边长为10,连接 , 则的最小值为 B、连接 , 则 C、连接 , 若 , , 则正方形的边长为 D、若M,N分别为的中点,存在点E,使得7. 如图,△ABC内接于⊙O,BC=6,AC=2,∠A-∠B=90°,则⊙O的面积为( )
A、若正方形的边长为10,连接 , 则的最小值为 B、连接 , 则 C、连接 , 若 , , 则正方形的边长为 D、若M,N分别为的中点,存在点E,使得7. 如图,△ABC内接于⊙O,BC=6,AC=2,∠A-∠B=90°,则⊙O的面积为( ) A、9.6π B、10π C、10.8π D、12π8. 如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
A、9.6π B、10π C、10.8π D、12π8. 如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( ) A、∠OBA=∠OCA B、四边形OABC内接于⊙O C、AB=2BC D、∠OBA+∠BOC=90°9. 已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )
A、∠OBA=∠OCA B、四边形OABC内接于⊙O C、AB=2BC D、∠OBA+∠BOC=90°9. 已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )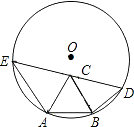 A、 B、1 C、 D、a10. 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
A、 B、1 C、 D、a10. 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空4分,共24分)
-
11. 如图,点A、B、C都在上,如果 , 那么的度数为.
 12. 如图,内接于 , 外角的平分线交于点 , 射线交延长线于点.若 , , 则的度数为°.
12. 如图,内接于 , 外角的平分线交于点 , 射线交延长线于点.若 , , 则的度数为°.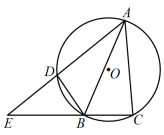 13. 若⊙O中,弦AB的长度是半径的倍,则弦AB所对圆周角的度数为°.14. ⊙为等边的外接圆,半径为2,点在劣弧上运动(不与点 , 重合),连结 , , .则四边形的面积关于线段的长的函数解析式是.
13. 若⊙O中,弦AB的长度是半径的倍,则弦AB所对圆周角的度数为°.14. ⊙为等边的外接圆,半径为2,点在劣弧上运动(不与点 , 重合),连结 , , .则四边形的面积关于线段的长的函数解析式是. 15. 如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD=2,E是AC的中点,连接DE,则线段DE长度的最小值为.
15. 如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD=2,E是AC的中点,连接DE,则线段DE长度的最小值为. 16. 如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;② ;③⊙O的直径为2;④AE=AD.其中正确的结论有(填序号).
16. 如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;② ;③⊙O的直径为2;④AE=AD.其中正确的结论有(填序号).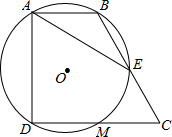
三、解答题(共8题,共66分)
-
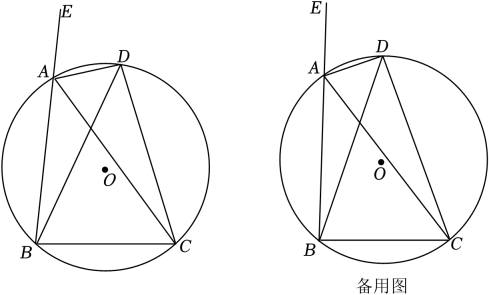
17. 如图所示,四边形是半径为R的的内接四边形,是的直径, , 直线l与三条线段、、的延长线分别交于点E、F、G.且满足 .
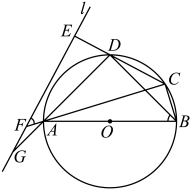 (1)、求证:直线直线;(2)、若;
(1)、求证:直线直线;(2)、若;①求证:;
②若 , 求四边形的周长.
18. 在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:已知:是等边三角形,点D是内一点,连接 , 将线段绕C逆时针旋转得到线段 , 连接 , , , 并延长交于点F.当点D在如图所示的位置时: (1)、观察填空:与全等的三角形是;(2)、利用(1)中的结论,求的度数(3)、判断线段 , , 之间的数量关系,并说明理由.19. 如图
(1)、观察填空:与全等的三角形是;(2)、利用(1)中的结论,求的度数(3)、判断线段 , , 之间的数量关系,并说明理由.19. 如图 (1)、如图1,在和中, , , .求证:;(2)、如图2,在和中, , , , , 点在内,延长交于点 , 求证:点是中点;(3)、如图3,为等腰三角形,. , 点为所在平面内一点, , , , 请直接写出的长.20. 已知:是的外接圆,且 , , D为上一动点.
(1)、如图1,在和中, , , .求证:;(2)、如图2,在和中, , , , , 点在内,延长交于点 , 求证:点是中点;(3)、如图3,为等腰三角形,. , 点为所在平面内一点, , , , 请直接写出的长.20. 已知:是的外接圆,且 , , D为上一动点. (1)、如图1,若点D是的中点,等于多少?(2)、过点B作直线的垂线,垂足为点E.
(1)、如图1,若点D是的中点,等于多少?(2)、过点B作直线的垂线,垂足为点E.①如图2,若点D在上,求证:.
②若点D在上,当它从点A向点C运动且满足时,求的最大值.
21. 已知内接于 , 的平分线交于点 , 连接 , . (1)、如图①,当时,请直接写出线段 , , 之间满足的等量关系式:;(2)、如图②,当时,试探究线段 , , 之间满足的等量关系,并证明你的结论.22. 如图,点P是等边三角形中边上的动点(),作的外接圆交于点D.点E是圆上一点,且 , 连接交于点F.
(1)、如图①,当时,请直接写出线段 , , 之间满足的等量关系式:;(2)、如图②,当时,试探究线段 , , 之间满足的等量关系,并证明你的结论.22. 如图,点P是等边三角形中边上的动点(),作的外接圆交于点D.点E是圆上一点,且 , 连接交于点F. (1)、求证:(2)、当点P运动变化时,的度数是否发生变化?若变化,请说明理由;若不变,求的度数.(3)、探究线段、、之间的数量关系,并证明.
(1)、求证:(2)、当点P运动变化时,的度数是否发生变化?若变化,请说明理由;若不变,求的度数.(3)、探究线段、、之间的数量关系,并证明.