2023年浙教版数学九年级上册3.5 圆周角 同步测试(提高版)
试卷更新日期:2023-08-06 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,在中, , 若 , 则的度数为( )
 A、 B、 C、 D、2. 如图,在等腰三角形ABC中,AB=AC,点D是AC的中点,若以AB为直径作圆,则下列判断正确的是( )
A、 B、 C、 D、2. 如图,在等腰三角形ABC中,AB=AC,点D是AC的中点,若以AB为直径作圆,则下列判断正确的是( ) A、点C一定在⊙O外 B、点C一定在⊙O上 C、点D一定在⊙O外 D、点D一定在⊙O上3. 如图, , , , , 过点作的平行线 , 为直线上一动点,为的外接圆,直线BP交于点,则的最小值为( )
A、点C一定在⊙O外 B、点C一定在⊙O上 C、点D一定在⊙O外 D、点D一定在⊙O上3. 如图, , , , , 过点作的平行线 , 为直线上一动点,为的外接圆,直线BP交于点,则的最小值为( ) A、 B、 C、 D、14. 如图,点、、是上的点, , 连结交于点 , 若 , 则的度数为( )
A、 B、 C、 D、14. 如图,点、、是上的点, , 连结交于点 , 若 , 则的度数为( ) A、 B、 C、 D、5. 如图,已知的半径为1,则它的内接正方形的边长为( )
A、 B、 C、 D、5. 如图,已知的半径为1,则它的内接正方形的边长为( )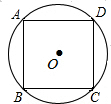 A、 B、2 C、1 D、6. 如图,是的直径,点 , 点是半圆上两点,连结 , 相交于点 , 连结 , 已知于点 , 下列结论:
A、 B、2 C、1 D、6. 如图,是的直径,点 , 点是半圆上两点,连结 , 相交于点 , 连结 , 已知于点 , 下列结论:
;若点为的中点,则.若 , 则;;其中正确的是( )
A、 B、 C、 D、7. 如图,已知是的直径,弦于点 , 是的中点,连结 , , , 则下列结论不一定成立的是( ) A、 B、 C、 D、8. 如图,已知是的直径,弦与交于点 , 设 , , , 则( )
A、 B、 C、 D、8. 如图,已知是的直径,弦与交于点 , 设 , , , 则( ) A、 B、 C、 D、9. 如图,⊙O是是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( )
A、 B、 C、 D、9. 如图,⊙O是是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( ) A、1 B、 C、2 D、10. 如图在△ABC中,边AB,AC的垂直平分线交于点P,连结BP,CP,若∠A=50°,则∠BPC=( )
A、1 B、 C、2 D、10. 如图在△ABC中,边AB,AC的垂直平分线交于点P,连结BP,CP,若∠A=50°,则∠BPC=( )
 A、100° B、95° C、90° D、50°
A、100° B、95° C、90° D、50°二、填空题(每空4分,共24分)
-
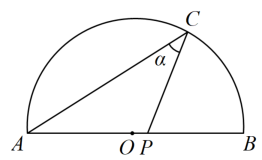
11. 如图,为的直径,点C在上,点Р在线段上运动(不与O,B重合),若 , 设为 , 则的取值范围是.
 12. 在圆中,四点在圆上, , , , 则的值为.
12. 在圆中,四点在圆上, , , , 则的值为.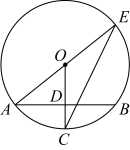 13. 已知D是内一点,E是的中点, , , , , 则.
13. 已知D是内一点,E是的中点, , , , , 则. 14. 如图,有一块三角板ABC,∠C为直角,∠ABC=30°,将它放置在0O中,点A,B在圆上,边BC经过圆心O,劣弧的度数是°.
14. 如图,有一块三角板ABC,∠C为直角,∠ABC=30°,将它放置在0O中,点A,B在圆上,边BC经过圆心O,劣弧的度数是°. 15. 如图,内接于半径为的半 , 为直径,点是的中点,连接交于点 , 平分交于点 , 且为的中点,则的长为.
15. 如图,内接于半径为的半 , 为直径,点是的中点,连接交于点 , 平分交于点 , 且为的中点,则的长为.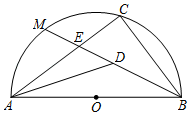 16. 如图,是的直径,C、D在上, , , 则长为.
16. 如图,是的直径,C、D在上, , , 则长为.
三、作图题(共8分)
-
17. 如图,在8x8的方格纸中,ΔABC的三个顶点都在格点上.
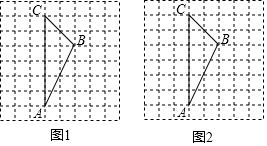 (1)、在图1中画出一个∠ADC,使得∠ADC=∠ABC,且点D为格点.(2)、在图2中画出一个∠CEB,使得∠CEB=2∠CAB,且点E为格点.
(1)、在图1中画出一个∠ADC,使得∠ADC=∠ABC,且点D为格点.(2)、在图2中画出一个∠CEB,使得∠CEB=2∠CAB,且点E为格点.四、解答题(共8题,共58分)
-
18. 如图,点E为 弦 的中点,过点O,E作直径 ,连接 ,过点C的弦 交 于G.求证: .
 19. 如图,为的直径,点在上,延长至点 , 使.延长与的另一个交点为 , 连结.
19. 如图,为的直径,点在上,延长至点 , 使.延长与的另一个交点为 , 连结. (1)、求证:;(2)、若 , 求的长.20. 如图,AB是半圆O的直径,C、D是半圆O上的两点,D为的中点,OD与AC交于点E.
(1)、求证:;(2)、若 , 求的长.20. 如图,AB是半圆O的直径,C、D是半圆O上的两点,D为的中点,OD与AC交于点E. (1)、证明:(2)、若∠B=70°,求∠CAD的度数;(3)、若AB=4,AC=3,求DE的长.21. 如图,△ABC内接于⊙O,AB是⊙O的直径,AB=10,AC=6. 连接OC,弦AD分别交OC,BC于点E,F,其中E是AD的中点.
(1)、证明:(2)、若∠B=70°,求∠CAD的度数;(3)、若AB=4,AC=3,求DE的长.21. 如图,△ABC内接于⊙O,AB是⊙O的直径,AB=10,AC=6. 连接OC,弦AD分别交OC,BC于点E,F,其中E是AD的中点. (1)、求证:∠CAD=∠CBA.(2)、求OE的长.22. 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,OD∥BC,
(1)、求证:∠CAD=∠CBA.(2)、求OE的长.22. 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,OD∥BC,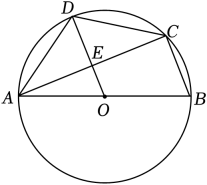 (1)、求证:AD=CD;(2)、若AC=8,DE=2,求BC的长.
(1)、求证:AD=CD;(2)、若AC=8,DE=2,求BC的长.
-


