2023年浙教版数学九年级上册3.4 圆心角 同步测试(提高版)
试卷更新日期:2023-08-06 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等,不正确的有( )A、2个 B、3个 C、4个 D、5个2. 如图,已知锐角 , 按如下步骤作图:(1)在射线上取一点 , 以点为圆心,长为半径作 , 交射线于点 , 连接;(2)分别以点 , 为圆心,长为半径作弧,交于点 , ;③连接 , , . 根据以上作图过程及所作图形,下列结论中错误的是( )
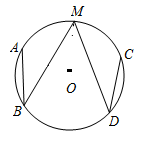
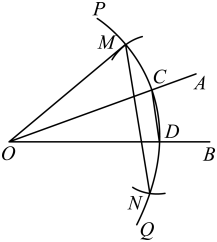 A、 B、若 , 则 C、 D、3. 如图,已知的半径为 , 、是直径的同侧圆周上的两点, , 是的中点,动点在线段上,则的最小值为( )
A、 B、若 , 则 C、 D、3. 如图,已知的半径为 , 、是直径的同侧圆周上的两点, , 是的中点,动点在线段上,则的最小值为( )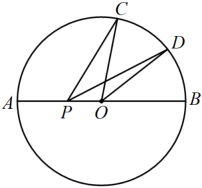 A、 B、 C、 D、4. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )
A、 B、 C、 D、4. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )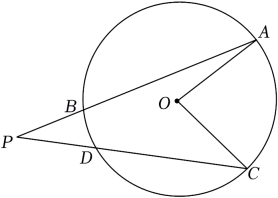 A、30° B、25° C、20° D、10°5. 如图,在 ⊙O中, , D、E分别是半径OA,OB的中点,连接OC,AC,BC,CD,CE,则下列结论不一定成立的是( )
A、30° B、25° C、20° D、10°5. 如图,在 ⊙O中, , D、E分别是半径OA,OB的中点,连接OC,AC,BC,CD,CE,则下列结论不一定成立的是( ) A、AC=BC B、CD=CE C、∠ACD=∠BCE D、CD⊥OA6. 如图,△ABC内接于圆O,AC=10,BC=24,且∠A=90°+∠B,则点O到AB的距离为( )
A、AC=BC B、CD=CE C、∠ACD=∠BCE D、CD⊥OA6. 如图,△ABC内接于圆O,AC=10,BC=24,且∠A=90°+∠B,则点O到AB的距离为( ) A、 B、 C、2.4 D、7. 如图,半径为5的 中,弦 , 所对的圆心角分别是 , .已知 , ,则弦 的弦心距等于
A、 B、 C、2.4 D、7. 如图,半径为5的 中,弦 , 所对的圆心角分别是 , .已知 , ,则弦 的弦心距等于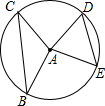 A、 B、 C、4 D、38. 如图, 是 的直径, , 是 的半径, ,点D在 上, ,点P是半径 上的一个动点,则 的最小值为( )
A、 B、 C、4 D、38. 如图, 是 的直径, , 是 的半径, ,点D在 上, ,点P是半径 上的一个动点,则 的最小值为( ) A、1 B、 C、 D、9. 如图,AB是⊙O的直径, = = ,∠COD=34°,则∠AEO的度数是( )
A、1 B、 C、 D、9. 如图,AB是⊙O的直径, = = ,∠COD=34°,则∠AEO的度数是( ) A、51° B、56° C、68° D、78°10. 如图,是半圆的直径,是弦,点是的中点,点是的中点,连接、分别交于点和点 , 连接 , 则下列结论中错误的是( )
A、51° B、56° C、68° D、78°10. 如图,是半圆的直径,是弦,点是的中点,点是的中点,连接、分别交于点和点 , 连接 , 则下列结论中错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空4分,共24分)
-
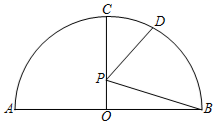
11. 在半径为1的圆中,长度等于的弦所对的弧的度数为 .12. 如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB, , 点P是OC上的一个动点,则BP+DP的最小值为 .
 13. 如图, 为 的直径, 点 是弧 的中点, 过点 作 于点 , 延长 交 于点 , 若 , 则 的半径长为
13. 如图, 为 的直径, 点 是弧 的中点, 过点 作 于点 , 延长 交 于点 , 若 , 则 的半径长为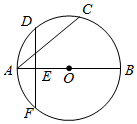 14. 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.若AC=10,DE=4,则BC的长为.
14. 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.若AC=10,DE=4,则BC的长为. 15. 如图所示,在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在PM以及⊙O的半径OM,OP上,并且∠POM=45°,则AB的长为 .
15. 如图所示,在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在PM以及⊙O的半径OM,OP上,并且∠POM=45°,则AB的长为 . 16. 如图所示,在⊙O中,C、D分别是OA、OB的中点,MC⊥AB、ND⊥AB,M、N在⊙O上.下列结论:
16. 如图所示,在⊙O中,C、D分别是OA、OB的中点,MC⊥AB、ND⊥AB,M、N在⊙O上.下列结论:
① ,
② ,
③四边形MCDN是正方形,
④MN= AB,
所有正确结论的序号是 .
三、作图题
-
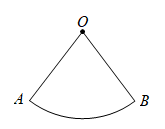
17. 如图,已知扇形 , 请用尺规作图,在上求作一点P,使(保留作图痕迹,不写作法).
四、解答题(共8题,共66分)
-
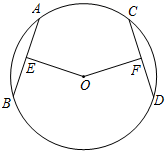
18. 如图,AB、CD是⊙O的两条弦,= , OE⊥AB,OF⊥CD,垂足分别为E、F.求证:OE=OF.
 19. 如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
19. 如图所示,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.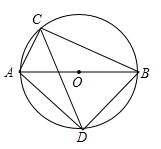 20. 如图所示,是的一条弦, ,垂足为 , 交于点、 .
20. 如图所示,是的一条弦, ,垂足为 , 交于点、 . (1)、若 ,求 的度数;(2)、若 , ,求的半径长;21. 如图所示,在△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长线交边AC于点D.
(1)、若 ,求 的度数;(2)、若 , ,求的半径长;21. 如图所示,在△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长线交边AC于点D. (1)、若∠ACB=60°,BC=8 , 求⊙O的半径;(2)、当△BCD是等腰三角形时,求∠BCD的大小.22. 如图,在中,B、C是的三等分点,弦相交于点E.
(1)、若∠ACB=60°,BC=8 , 求⊙O的半径;(2)、当△BCD是等腰三角形时,求∠BCD的大小.22. 如图,在中,B、C是的三等分点,弦相交于点E.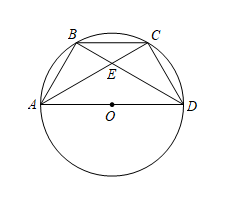 (1)、求证:;(2)、连接 , 若 , 求的度数.
(1)、求证:;(2)、连接 , 若 , 求的度数.
-