2023-2024学年高中数学人教A版选择性必修一 1.4 空间向量的应用
试卷更新日期:2023-08-06 类型:同步测试
一、选择题
-
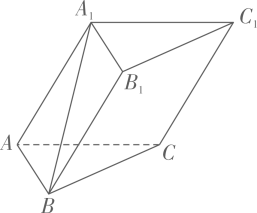
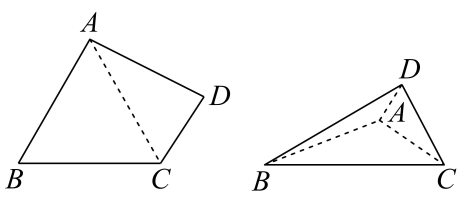
1. 已知直线 , 的方向向量分别为 , , 则直线 , 夹角的余弦值为( )A、 B、 C、 D、2. 已知 , , , 则平面ABC的一个法向量可以是( )A、 B、 C、 D、3. 在《九章算术》中,将四个面都是直角三角形的四面体称为“鳖臑”,在“鳖臑”中,平面 , , 且 , 为的中点,则异面直线与夹角的余弦值为( )A、 B、 C、 D、4. 若直线l的方向向量与平面的法向量的夹角等于 , 则直线l与平面所成的角等于( )A、 B、 C、 D、5. 如图,为直角梯形,.连 , 将沿翻折成三棱锥 , 当三棱锥外接球表面积的最小值时,二面角的余弦值为( )
 A、 B、0 C、 D、6. 如图,正方体的棱长为2,线段上有两个动点(在的左边),且 . 下列说法不正确的是( )
A、 B、0 C、 D、6. 如图,正方体的棱长为2,线段上有两个动点(在的左边),且 . 下列说法不正确的是( ) A、当运动时,二面角的最小值为 B、当运动时,三棱锥体积不变 C、当运动时,存在点使得 D、当运动时,二面角为定值7. 若直线的方向向量为 , 平面的法向量为 , 则能使∥的是( )A、 B、 C、 D、8. 在四棱锥中,底面 , 底面是边长为的正方形, , 则直线与平面所成角的正弦值为( )A、 B、 C、 D、9. 如图,直线平面 , 垂足为 , 正四面体(所有棱长都相等的三棱锥)的棱长为2,在平面内,是直线上的动点,当到的距离最大时,该正四面体在平面上的射影面积为( )
A、当运动时,二面角的最小值为 B、当运动时,三棱锥体积不变 C、当运动时,存在点使得 D、当运动时,二面角为定值7. 若直线的方向向量为 , 平面的法向量为 , 则能使∥的是( )A、 B、 C、 D、8. 在四棱锥中,底面 , 底面是边长为的正方形, , 则直线与平面所成角的正弦值为( )A、 B、 C、 D、9. 如图,直线平面 , 垂足为 , 正四面体(所有棱长都相等的三棱锥)的棱长为2,在平面内,是直线上的动点,当到的距离最大时,该正四面体在平面上的射影面积为( ) A、 B、 C、 D、10. 已知是直线l的方向向量,是平面的法向量.若 , 则下列选项正确的是( )A、 B、 C、 D、11. 已知正方体的棱长为1,点在线段上,有下列四个结论:
A、 B、 C、 D、10. 已知是直线l的方向向量,是平面的法向量.若 , 则下列选项正确的是( )A、 B、 C、 D、11. 已知正方体的棱长为1,点在线段上,有下列四个结论:①;
②点到平面的距离为;
③二面角的余弦值为;
④若四面体的所有顶点均在球的球面上,则球的体积为.
其中所有正确结论的个数是( )
A、1 B、2 C、3 D、412. 如图,在长方体中, , , 为棱上一点,且 , 平面上一动点满足 , 设是该长方体外接球上一点,则 , 两点间距离的最大值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、多项选择题
-
13. 如图,已知正方体的棱长为 , 、分别为棱、的中点,则下列结论正确的为( )
 A、 B、 C、 D、为平面的一个法向量14. 在正方体中, , , 则( )A、为钝角 B、 C、平面 D、直线与平面所成角的正弦值为15. 已知正方体的棱长为 , 为棱的中点,点满足 , 其中 , , 则( )
A、 B、 C、 D、为平面的一个法向量14. 在正方体中, , , 则( )A、为钝角 B、 C、平面 D、直线与平面所成角的正弦值为15. 已知正方体的棱长为 , 为棱的中点,点满足 , 其中 , , 则( ) A、当时,平面 B、当时, C、当时,三棱锥的体积是定值 D、当点落在以为球心,为半径的球面上时,的取值范围是16. 已知正四面体的棱长为分别为正四面体棱的中点,为面内任意一点,则下列结论正确的是( )A、平面截正四面体的外接球所得截面的面积为 B、若存在 , 使得 , 则线段长度的最小值为 C、过点作平面平面 , 若平面平面 , 平面平面 , 则所成角的正弦值为 D、平面与平面夹角的余弦值为
A、当时,平面 B、当时, C、当时,三棱锥的体积是定值 D、当点落在以为球心,为半径的球面上时,的取值范围是16. 已知正四面体的棱长为分别为正四面体棱的中点,为面内任意一点,则下列结论正确的是( )A、平面截正四面体的外接球所得截面的面积为 B、若存在 , 使得 , 则线段长度的最小值为 C、过点作平面平面 , 若平面平面 , 平面平面 , 则所成角的正弦值为 D、平面与平面夹角的余弦值为三、填空题
-
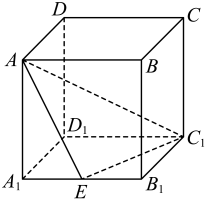
17. 如图,在棱长为1的正方体中,E为线段的中点,则点C到平面的距离等于.
 18. 已知向量是直线的一个方向向量,向量是平面的一个法向量,若直线⊥平面 , 则实数的值为.19. 已知长方体的底面是边长为的正方形,若 , 则该长方体的外接球的表面积为;记分别是方向上的单位向量,且 , , 则(m,n为常数)的最小值为 .20. 在空间直角坐标系中,已知点 , , , 则点到平面的距离为.21. 若空间中有三点 , 则到直线的距离为;点到平面的距离为.22. 如图,正方体的棱长为 , 若空间中的动点满足 , , 则下列命题正确的是 . (请用正确命题的序号作答)
18. 已知向量是直线的一个方向向量,向量是平面的一个法向量,若直线⊥平面 , 则实数的值为.19. 已知长方体的底面是边长为的正方形,若 , 则该长方体的外接球的表面积为;记分别是方向上的单位向量,且 , , 则(m,n为常数)的最小值为 .20. 在空间直角坐标系中,已知点 , , , 则点到平面的距离为.21. 若空间中有三点 , 则到直线的距离为;点到平面的距离为.22. 如图,正方体的棱长为 , 若空间中的动点满足 , , 则下列命题正确的是 . (请用正确命题的序号作答)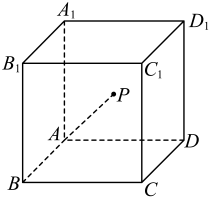
①若 , 则点到平面的距离为;
②若 , 则二面角的平面角为;
③若 , 则三棱锥的体积为;
④若 , 则点的轨迹构成的平面图形的面积为 .
四、解答题
-
23. 如图,在四棱锥中,平面平面 , , , .
 (1)、求证:平面;(2)、求点到平面的距离;(3)、求平面与平面的夹角.24. 如图,在矩形中, , , 点是边上的动点,沿将翻折至 , 使二面角为直二面角.
(1)、求证:平面;(2)、求点到平面的距离;(3)、求平面与平面的夹角.24. 如图,在矩形中, , , 点是边上的动点,沿将翻折至 , 使二面角为直二面角. (1)、当时,求证:;(2)、当线段的长度最小时,求二面角的正弦值.25. 如图,正方形是圆柱的轴截面,是圆柱的母线,圆柱的体积为 .
(1)、当时,求证:;(2)、当线段的长度最小时,求二面角的正弦值.25. 如图,正方形是圆柱的轴截面,是圆柱的母线,圆柱的体积为 . (1)、求圆柱的表面积;(2)、若 , 求点到平面的距离.
(1)、求圆柱的表面积;(2)、若 , 求点到平面的距离.