2023年浙教版数学七年级上册第三章 实数 章末检测(B卷)
试卷更新日期:2023-08-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列说法正确的是( )A、4的平方根是2 B、8的立方根是±2 C、如果一个数的立方根是这个数本身,那么这个数是-1,0或1 D、如果一个数的平方根是这个数本身,那么这个数是1或02. 下列四个式子:
① ;② <8;③ <1;④ >0.5.
其中大小关系正确的式子的个数是( )
A、1个 B、2个 C、3个 D、4个3. 已知|x|=6,y2=4,且xy<0.则x+y的值为( )A、4 B、-4 C、4或-4 D、2或-24. 若 , , 且 , 则的值是( )A、1或7 B、-1或7 C、1或-7 D、-1或-75. 设面积为31的正方形的边长为x,则x的取值范围是( )A、5.0 B、5.2 C、5.5 D、6. 若m=5n(m、n是正整数),且 ,则与实数 的最大值最接近的数是( )A、4 B、5 C、6 D、77. 如图,A、B两点在数轴上表示的数分别为a、b,以下结论:①a﹣b>0;②a+b<0;③(b﹣1)(a+1)>0;④ .其中结论正确的是( ) A、①② B、③④ C、①③ D、①②④8. 设681×2019﹣681×2018=a , 2015×2016﹣2013×2018=b , ,则a , b , c的大小关系是( )A、b<c<a B、a<c<b C、b<a<c D、c<b<a9. 数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.
A、①② B、③④ C、①③ D、①②④8. 设681×2019﹣681×2018=a , 2015×2016﹣2013×2018=b , ,则a , b , c的大小关系是( )A、b<c<a B、a<c<b C、b<a<c D、c<b<a9. 数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.①
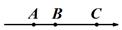 ②
② 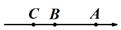 ③
③ 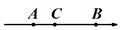 ④
④ 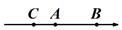 A、1个 B、2个 C、3个 D、4个10. 已知 , , 表示取三个数中最小的那个数﹒例如:当 , , , = , , =3﹒当 , , = 时,则 的值为( )A、 B、 C、 D、
A、1个 B、2个 C、3个 D、4个10. 已知 , , 表示取三个数中最小的那个数﹒例如:当 , , , = , , =3﹒当 , , = 时,则 的值为( )A、 B、 C、 D、二、填空题(每空2分,共20分)
-
11. 若一个正数的平方根是3a-2和5,则这个正数是 .12. 若某个正数的两个平方根分别为与 , 则的值是.13. 可以作为“两个无理数的和仍为无理数”的反例的是 .14. 如图,是一个计算程序.若输入的值为 , 则输出的结果为.
 15. 如图,数轴上点A到点B的距离与点B到点C的距离相等,若点B表示1,点C表示 , 则点A表示的数是 .
15. 如图,数轴上点A到点B的距离与点B到点C的距离相等,若点B表示1,点C表示 , 则点A表示的数是 . 16. 如图.方格的每一方格的边长为1个单位.依次连接各边的中点 . 则数轴上点对应的数是 , 线段长是 . 以顶点C为圆心.长为半径画圆交数轴于点 , 则数轴上点对应的无理数是 .
16. 如图.方格的每一方格的边长为1个单位.依次连接各边的中点 . 则数轴上点对应的数是 , 线段长是 . 以顶点C为圆心.长为半径画圆交数轴于点 , 则数轴上点对应的无理数是 . 17. 任何实数a,可用[a]表示不大于a的最大整数,如[4]=4, ,现对72进行如下操作:72→ =8→ → =1,类似地:
17. 任何实数a,可用[a]表示不大于a的最大整数,如[4]=4, ,现对72进行如下操作:72→ =8→ → =1,类似地:( 1 )对64只需进行次操作后变为1;
( 2 )只需进行3次操作后变为1的所有正整数中,最大的是.
三、解答题(共8题,共70分)
-
18. 计算:(1)、;(2)、;(3)、(4)、19. 课堂上,老师让同学们从下列数中找一个无理数: , , , 0, , ;其中,甲说“”,乙说“”,丙说“”.
 (1)、甲、乙、丙三个人中,说错的是.(2)、请将老师所给的数字按要求填入下面相应的区域内:20. 已知4的算术平方根是的平方根是是 的整数部分,(1)、求的值.(2)、求的平方根.21. 讲解完本节,王老师在小结时总结了这样一句话:“对于任意两个整数a、b,如果a>b,那么 > .”然后讲了下面的一个例题:比较 和 的大小.
(1)、甲、乙、丙三个人中,说错的是.(2)、请将老师所给的数字按要求填入下面相应的区域内:20. 已知4的算术平方根是的平方根是是 的整数部分,(1)、求的值.(2)、求的平方根.21. 讲解完本节,王老师在小结时总结了这样一句话:“对于任意两个整数a、b,如果a>b,那么 > .”然后讲了下面的一个例题:比较 和 的大小.方法一: = = , = = ,
又∵8<12,
∴ < .
方法二: = ×200=8, =4×3=12.
又∵8<12,
∴ < .
根据上面的例题解答下列各题:
(1)、比较 和 的大小;(2)、比较 ﹣1与 ﹣ 的大小.22. 阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来.于是小明用(-1)来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵<< , 即∵2<<3,
∴的整数部分是2,小数部分为(-2).
(1)、的整数部分是 , 小数部分是 .(2)、的小数部分为a,的整数部分为b,则a+b-的值;(3)、已知: , 其中x是整数,且 , 求的值.23. 据说我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求出它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥妙,华罗庚讲述了计算过程:第一步:因为 , , , 所以 .
第二步:因为59319的个位上的数是9,只有个位数字是9的数的立方的个位数字是9,所以的个位数字是9.
第三步:如果划去59319后面的三位319得到数59,而 , , 所以 ,
所以 , 即的十位数字是3.
所以 .
请根据上述材料解答下列问题:
(1)、用上述方法确定4913的立方根的个位数字是 .(2)、用上述方法确定50653的立方根是 .(3)、求的值,要求写出计算过程.24. 观察下边图形,每个小正方形的边长为1.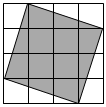 (1)、则图中阴影部分的面积是 , 边长是.(2)、已知阴影正方形的边长为 , 且 , 若和是相邻的两个整数,那么 , .(3)、若设如图阴影正方形的边长为 , 请在下面的数轴上准确地作出数所表示的点,若还有一个点与它的距离为1,则这个点在数轴上所表示的数为.
(1)、则图中阴影部分的面积是 , 边长是.(2)、已知阴影正方形的边长为 , 且 , 若和是相邻的两个整数,那么 , .(3)、若设如图阴影正方形的边长为 , 请在下面的数轴上准确地作出数所表示的点,若还有一个点与它的距离为1,则这个点在数轴上所表示的数为. 25. 如图,直径为1个单位长度的圆片上有一点 与数轴上的原点重合.(所有结果均保留 )
25. 如图,直径为1个单位长度的圆片上有一点 与数轴上的原点重合.(所有结果均保留 )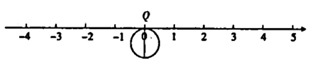 (1)、若该圆片从原点沿数轴向左滚动一周,圆片上与原点重合的点 到达点 ,设点 表示的数为 .
(1)、若该圆片从原点沿数轴向左滚动一周,圆片上与原点重合的点 到达点 ,设点 表示的数为 .①求 的值;
②求 的算术平方根.
(2)、若圆片在数轴上向右滚动的周数记为正数,向左滚动的周数记为负数,依次滚动的情况记录如下:+2,-1,+3,-4,-3.①第几次滚动后,点 距离原点最近?第几次滚动后,点 距离原点最远?
②当圆片结束运动时,点 运动的路程共有多少?此时点 所表示的数是多少?