2023年浙教版数学七年级上册3.2 实数 同步测试(培优版)
试卷更新日期:2023-08-06 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 下列四个式子:
① ;② <8;③ <1;④ >0.5.
其中大小关系正确的式子的个数是( )
A、1个 B、2个 C、3个 D、4个2. 实数a , b , c在数轴上的对应点的位置如图所示.下列式子正确的是( ) A、 B、 C、 D、3. 若m=5n(m、n是正整数),且 ,则与实数 的最大值最接近的数是( )A、4 B、5 C、6 D、74. 根据表中的信息判断,下列语句正确的是( )
A、 B、 C、 D、3. 若m=5n(m、n是正整数),且 ,则与实数 的最大值最接近的数是( )A、4 B、5 C、6 D、74. 根据表中的信息判断,下列语句正确的是( )n
256
259.21
262.44
265.69
268.96
272.25
275.56
16
16.1
16.2
16.3
16.4
16.5
16.6
A、 B、 C、只有3个正整数n满足 D、5. 如图,A、B两点在数轴上表示的数分别为a、b,以下结论:①a﹣b>0;②a+b<0;③(b﹣1)(a+1)>0;④ .其中结论正确的是( ) A、①② B、③④ C、①③ D、①②④6. 设681×2019﹣681×2018=a , 2015×2016﹣2013×2018=b , ,则a , b , c的大小关系是( )A、b<c<a B、a<c<b C、b<a<c D、c<b<a7. 数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.
A、①② B、③④ C、①③ D、①②④6. 设681×2019﹣681×2018=a , 2015×2016﹣2013×2018=b , ,则a , b , c的大小关系是( )A、b<c<a B、a<c<b C、b<a<c D、c<b<a7. 数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.①
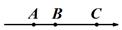 ②
② 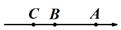 ③
③ 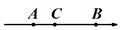 ④
④ 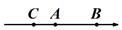 A、1个 B、2个 C、3个 D、4个8. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
A、1个 B、2个 C、3个 D、4个8. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )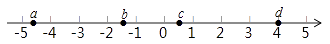 A、a>–4 B、bd>0 C、|a|>|d| D、b+c>09. 已知 , , 表示取三个数中最小的那个数﹒例如:当 , , , = , , =3﹒当 , , = 时,则 的值为( )A、 B、 C、 D、10. 对于实数x,我们规定[x]表示不大于x的最大整数,如[4]=4,[ ]=1,[﹣2.5]=﹣3.现对82进行如下操作:82 [ ]=9 [ ]=3 [ ]=1,这样对82只需进行3次操作后变为1,类似地,对121只需进行多少次操作后变为1( )A、1 B、2 C、3 D、4
A、a>–4 B、bd>0 C、|a|>|d| D、b+c>09. 已知 , , 表示取三个数中最小的那个数﹒例如:当 , , , = , , =3﹒当 , , = 时,则 的值为( )A、 B、 C、 D、10. 对于实数x,我们规定[x]表示不大于x的最大整数,如[4]=4,[ ]=1,[﹣2.5]=﹣3.现对82进行如下操作:82 [ ]=9 [ ]=3 [ ]=1,这样对82只需进行3次操作后变为1,类似地,对121只需进行多少次操作后变为1( )A、1 B、2 C、3 D、4二、填空题(每空4分,共20分)
-
11. 如图,把半径为1的圆从数轴上表示-1的点A开始沿数轴向右滚动一周,圆上的点A到达点 , 则点表示的数为 .
 12. 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是;点B表示的数是 .
12. 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是;点B表示的数是 . 13. 若 , , ,则 的大小关系用“<”号排列为 .14. 已知 , , , . 若n为整数且 , 则n的值为 .15. 阅读下列材料:因为 , 即 , 所以的整数部分为2,小数部分为 , 若规定实数m的整数部分记为 , 小数部分记为 , 可得: , . 按照此规定计算的值 .
13. 若 , , ,则 的大小关系用“<”号排列为 .14. 已知 , , , . 若n为整数且 , 则n的值为 .15. 阅读下列材料:因为 , 即 , 所以的整数部分为2,小数部分为 , 若规定实数m的整数部分记为 , 小数部分记为 , 可得: , . 按照此规定计算的值 .三、解答题(共8题,共70分)
-
16. 课堂上老师讲解了比较 和 的方法,观察发现11-10=15-14=1,于是比较这两个数的倒数:
因为 ,所以 ,则有 ,
请你设计一种方法比较 与 的大小,
17. 下面是小李同学探索的近似数的过程:∵面积为107的正方形边长是 , 且 ,
∴设 , 其中0<x<1,画出如图示意图,
∵图中S正方形=102+2×10•x+x2 , S正方形=107
∴102+2×10•x+x2=107
当x2较小时,省略x2 , 得20x+100≈107,得到x≈0.35,即 .
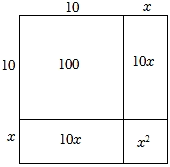 (1)、的整数部分是;(2)、仿照上述方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)18. 阅读下面求 近似值的方法,回答问题:
(1)、的整数部分是;(2)、仿照上述方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)18. 阅读下面求 近似值的方法,回答问题:①任取正数 ;
②令 则 ;
③ ,则 ;
……以此类推 次,得到
其中 称为 的 阶过剩近似值, 称为 的 阶不足近似值.仿照上述方法,求6的近似值.
①取正数 .
②于是 a2= ;则
③ 的3阶过剩近似值 是 , 3阶不足近似值是
19. 阅读下面材料:随着人们认识的不断深入,毕达哥拉斯学派逐渐承认 不是有理数,并给出了证明.假设是 有理数,那么存在两个互质的正整数p,q,使得 = ,于是p= q,两边平方得p2=2q2 . 因为2q2是偶数,所以p2是偶数,而只有偶数的平方才是偶数,所以p也是偶数.因此可设p=2s,代入上式,得4s2=2q2 , 即q2=2s2 , 所以q也是偶数,这样,p和q都是偶数,不互质,这与假设p,q互质矛盾,这个矛盾说明, 不能写成分数的形式,即 不是有理数.请你有类似的方法,证明 不是有理数.
20. 操作探究:已知在纸面上有一数轴(如图所示) (1)、折叠纸面,使表示的点1与﹣1重合,则﹣2表示的点与表示的点重合;(2)、折叠纸面,使﹣1表示的点与3表示的点重合,回答以下问题:
(1)、折叠纸面,使表示的点1与﹣1重合,则﹣2表示的点与表示的点重合;(2)、折叠纸面,使﹣1表示的点与3表示的点重合,回答以下问题:①5表示的点与数表示的点重合;
② 表示的点与数表示的点重合;
③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是、点B表示的数是
(3)、已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值.21. 对于任何实数 , 可用表示不超过的最大整数,如.(1)、则;;(2)、现对119进行如下操作: , 这样对119只需进行3次操作后变为1.对15进行1次操作后变为 ▲ , 对200进行3次操作后变为 ▲ ;
对实数恰进行2次操作后变成1,则最小可以取到 ▲ ;
若正整数进,3次操作后变为1,求的最大值.
22. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.小白在草稿纸上画了一条数轴进行操作探究: (1)、操作一:折叠纸面,若使表示的点1与﹣1表示的点重合,则﹣2表示的点与表示的点重合;(2)、操作二:折叠纸面,若使1表示的点与﹣3表示的点重合,回答以下问题:
(1)、操作一:折叠纸面,若使表示的点1与﹣1表示的点重合,则﹣2表示的点与表示的点重合;(2)、操作二:折叠纸面,若使1表示的点与﹣3表示的点重合,回答以下问题:① 表示的点与数表示的点重合;
②若数轴上A、B两点之间距离为8(A在B的左侧),且A、B两点经折叠后重合,则A、B两点表示的数分别是;
(3)、操作三:在数轴上剪下9个单位长度(从﹣1到8)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(如图). 若这三条线段的长度之比为1:1:2,则折痕处对应的点所表示的数可能是.23. 如图,在数轴上有两个长方形ABCD和EFGH,这两个长方形的宽都是2 个单位长度, 长方形ABCD的长AD是4 个单位长度,长方形EFGH的长EH是8 个单位长度,点E在数轴上表示的数是5 ,且E、D两点之间的距离为12 。 (1)、点H在数轴上表示的数是点,点A在数轴上表示的数是。(2)、若线段AD的中点为M,线段EH上有一点N,EN= EH,M以每秒4个单位长度的速度向右匀速运动,N以每秒3个单位长度的速度向左运动,设运动的时间为x秒,问当x为多少时,原点O恰为线段MN的三等分点?(3)、若线段AD的中点为M,线段EH上有一点N,EN= EH,长方形ABCD以每秒4个单位长度的速度向右匀速运动,长方形EFGH保持不动,设运动时间为t秒,是否存在一个t的值,使以M、N、F三点为顶点的三角形是直角三角形?若存在,求t的值;不存在,请说明理由。
(1)、点H在数轴上表示的数是点,点A在数轴上表示的数是。(2)、若线段AD的中点为M,线段EH上有一点N,EN= EH,M以每秒4个单位长度的速度向右匀速运动,N以每秒3个单位长度的速度向左运动,设运动的时间为x秒,问当x为多少时,原点O恰为线段MN的三等分点?(3)、若线段AD的中点为M,线段EH上有一点N,EN= EH,长方形ABCD以每秒4个单位长度的速度向右匀速运动,长方形EFGH保持不动,设运动时间为t秒,是否存在一个t的值,使以M、N、F三点为顶点的三角形是直角三角形?若存在,求t的值;不存在,请说明理由。