广东省历年（2019-2023年）中考数学真题分类汇编14 统计与概率

试卷更新日期：2023-08-06 类型：二轮复习

进入出卷网下载

一、选择题

1. 下表为五种运动耗氧情况，其中耗氧量的中位数是（）.

打网球	跳绳	爬楼梯	慢跑	游泳
$80 L / h$	$90 L / h$	$105 L / h$	$110 L / h$	$115 L / h$

A、

80 L / h

B、

107.5 L / h

C、

105 L / h

D、

110 L / h

查看试题解析

2. 空气是由多种气体混合而成的，为了直观地介绍空气各成分的百分比，最适合使用的统计图是（）

A、条形图 B、扇形图 C、折线图 D、频数分布直方图

查看试题解析
3. 同时掷两枚质地均匀的骰子，则两枚骰子向上的点数之和为7的概率是（）

A、 $\frac{1}{12}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 《你好，李焕英》的票房数据是：109，133，120，118，124，那么这组数据的中位数是（）

A、124 B、120 C、118 D、109

查看试题解析
5. 这组数据20，21，22，23，23的中位数和众数分别是（）

A、20，23 B、21，23 C、21，22 D、22，23

查看试题解析
6. 广州正稳步推进碧道建设，营造“水清岸绿、鱼翔浅底、水草丰美、白鹭成群”的生态廊道，使之成为老百姓美好生活的好去处，到今年底各区完成碧道试点建设的长度分别为（单位：千米）：5，5.2，5，5，5，6.4，6，5，6.68，48.4，6.3，这组数据的众数是（）

A、5 B、5.2 C、6 D、6.4

查看试题解析
7. 某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习，每门课程被选中的可能性相等，小明恰好选中“烹饪”的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
8. 为了庆祝中国共产党成立100周年，某校举办了党史知识竞赛活动，在获得一等奖的学生中，有3名女学生，1名男学生，则从这4名学生中随机抽取2名学生，恰好抽到2名女学生的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
9. 某同学在今年的中考体育测试中选考跳绳．考前一周，他记录了自己五次跳绳的成绩（次数/分钟）：247，253，247，255，263．这五次成绩的平均数和中位数分别是（）

A、253，253 B、255，253 C、253，247 D、255，247

查看试题解析
10. 某校饭堂随机抽取了100名学生，对他们最喜欢的套餐种类进行问卷调查后（每人选一种），绘制了如图的条形统计图，根据图中的信息，学生最喜欢的套餐种类是（）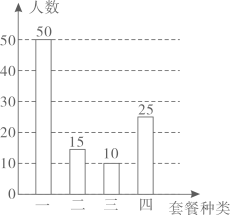

A、套餐一 B、套餐二 C、套餐三 D、套餐四

查看试题解析
11. 一组数据2，4，3，5，2的中位数是（）

A、5 B、35 C、3 D、25

查看试题解析
12. 数据3、3、5、8、11的中位数是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

13. 小明从《红星照耀中国》，《红岩》，《长征》，《钢铁是怎样炼成的》四本书中随机挑选一本，其中拿到《红星照耀中国》这本书的概率为．

查看试题解析
14. 现有8张同样的卡片，分别标有数字：1，1，2，2，2，3，4，5，将这些卡片放在一个不透明的盒子里，搅匀后从中随机地抽出一张，抽到标有数字2的卡片的概率是．

查看试题解析
15. 口袋内装有编号分别为1，2，3，4，5，6，7的七个球（除编号外都相同），从中随机摸出一个球，则摸出编号为偶数的球的概率是．

查看试题解析

三、解答题

16. 为了提高某城区居民的生活质量，政府将改造城区配套设施，并随机向某居民小区发放调查问卷（1人只能投1票），共有休闲设施，儿童设施，娱乐设施，健身设施4种选项，一共调查了a人，其调查结果如下：

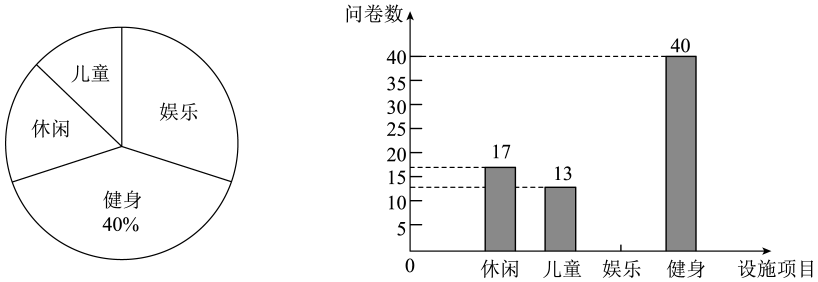
如图，为根据调查结果绘制的扇形统计图和条形统计图，请根据统计图回答下面的问题：

①调查总人数 $a =$ 人；

②请补充条形统计图；

③若该城区共有10万居民，则其中愿意改造“娱乐设施”的约有多少人？

④改造完成后，该政府部门向甲、乙两小区下发满意度调查问卷，其结果（分数）如下：

项目

小区

休闲

儿童

娱乐

健身

甲

乙

若以1：1：1：1进行考核，小区满意度（分数）更高；

若以1：1：2：1进行考核，小区满意度（分数）更高．

查看试题解析

四、综合题

17. 小红家到学校有两条公共汽车线路，为了解两条线路的乘车所用时间，小红做了试验，第一周(5个工作日)选择A线路，第二周(5个工作日)选择B线路，每天在固定时间段内乘车2次并分别记录所用时间，数据统计如下：(单位：min)

数据统计表

试验序号	1	2	3	4	5	6	7	8	9	10
A线路所用时间	15	32	15	16	34	18	21	14	35	20
B线路所用时间	25	29	23	25	27	26	31	28	30	24

数据折线统计图

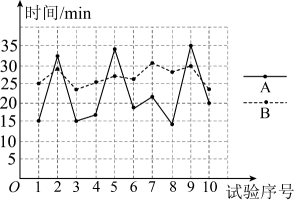
根据以上信息解答下列问题：

	平均数	中位数	众数	方差
A线路所用时间	22	a	15	63.2
B线路所用时间	b	26.5	c	6.36

(1)、填空：

a =

；

b =

；

c =

；

(2)、应用你所学的统计知识，帮助小红分析如何选择乘车线路．

查看试题解析

18. 某中学为了解初三学生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下：3；5；3；6；3；4；4；5；2；4；5；6；1；3；5；5；4；4；2；4
根据以上数据，得到如下不完整的频数分布表：

次数

1

2

3

4

5

6

人数

1

2

a

6

b

2

(1)、表格中的 $a =$ ， $b =$ ；

(2)、在这次调查中，参加志愿者活动的次数的众数为，中位数为；

(3)、若该校初三年级共有300名学生，根据调查统计结果，估计该校初三年级学生参加志愿者活动的次数为4次的人数．

查看试题解析
19. 某中学九年级举办中华优秀传统文化知识竞赛．用简单随机抽样的方法，从该年级全体600名学生中抽取20名，其竞赛成绩如图：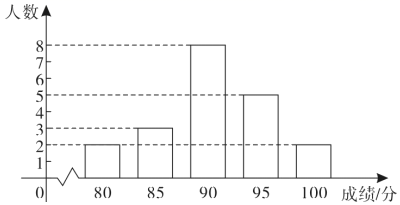

(1)、求这20名学生成绩的众数，中位数和平均数；

(2)、若规定成绩大于或等于90分为优秀等级，试估计该年级获优秀等级的学生人数．

查看试题解析

20. 随机调查某城市30天空气质量指数（

A Q I

），绘制成如下扇形统计图．

空气质量等级	空气质量指数（ $A Q I$ ）	频数
优	$A Q I ⩽ 50$	m
良	$50 < A Q I ⩽ 10000$	15
中	$100 < A Q I ⩽ 150$	9
差	$A Q I > 150$	n

(1)、

m =

，

n =

；

(2)、求良的占比；

(3)、求差的圆心角；

(4)、折线图是一个月内的空气污染指数统计，然后根据这个一个月内的统计进行估测一年的空气污染指数为中的天数，从折线图可以得到空气污染指数为中的有9天．

根据折线统计图，一个月（30天）中有天AQI为中，估测该城市一年（以365天计）中大约有天 $A Q I$ 为中．

查看试题解析

21. 以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业态发展对人才的需求更加旺盛．某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生，现随机调査了m名新聘毕业生的专业情况，并将调查结果绘制成如下两幅不完整的统计图：

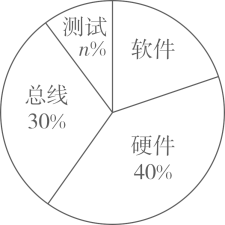
根据以上信息，解答下列问题：

(1)、m= ， n=；

(2)、请补全条形统计图；

(3)、在扇形统计图中，“软件”所对应圆心角的度数是；

(4)、若该公司新聘600名毕业生，请你估计“总线”专业的毕业生有名．

查看试题解析

22. 为了更好地解决养老问题，某服务中心引入优质社会资源为甲，乙两个社区共30名老人提供居家养老服务，收集得到这30名老人的年龄（单位：岁）如下：

甲社区	67	68	73	75	76	78	80	82	83	84	85	85	90	92	95
乙社区	66	69	72	74	75	78	80	81	85	85	88	89	91	96	98

根据以上信息解答下列问题：

(1)、求甲社区老人年龄的中位数和众数；

(2)、现从两个社区年龄在70岁以下的4名老人中随机抽取2名了解居家养老服务情况，求这2名老人恰好来自同一个社区的概率．

查看试题解析

23. 某中学开展主题为“垃圾分类知多少”的调查活动，调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，要求每名学生选且只能选其中一个等级．随机抽取了120名学生的有效问卷，数据整理如下：

等级

非常了解

比较了解

基本了解

不太了解

人数（人）

24

72

18

$x$

(1)、求 $x$ 的值；

(2)、若该校有学生1800人，请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人？

查看试题解析
24. 某校为了解学生对中国民族乐器的喜爱情况，随机抽取了本校的部分学生进行调查（每名学生选择并且只能选择一种喜爱的乐器)，现将收集的数据绘制成如下两幅不完整的统计图．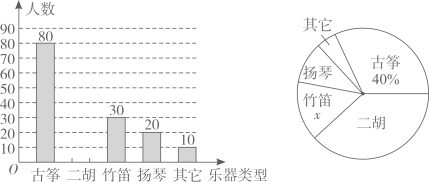

(1)、这次共抽取名学生进行调查，扇形统计图中的x=：

(2)、请补全统计图；

(3)、在扇形统计图中“扬琴”所对扇形的圆心角是度；

(4)、若该校有3000名学生，请你估计该校喜爱“二胡”的学生约有名．

查看试题解析

25. 某中学抽取了40名学生参加“平均每周课外阅读时间”的调查，由调查结果绘制了如下不完整的频数分布表和扇形统计图.

组别	时间/小时	频数/人数
A组	$0 \leq t < 1$	2
B组	$1 \leq t < 2$	m
C组	$2 \leq t < 3$	10
D组	$3 \leq t < 4$	12
E组	$4 \leq t < 5$	7
F组	$t \geq 5$	4

频数分布表

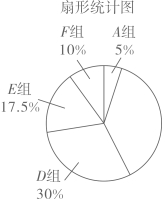
请根据图表中的信息解答下列问题：

(1)、求频数分布表中m的值；

(2)、求B组，C组在扇形统计图中分别对应扇形的圆心角度数，并补全扇形统计图；

(3)、已知F组的学生中，只有1名男生，其余都是女生，用列举法求以下事件的概率：从F组中随机选取2名学生，恰好都是女生。

查看试题解析

26. 为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为 $A$ 、 $B$ 、 $C$ 、 $D$ 四个等级，绘制如下不完整的统计图表，如题图表所示，根据图表信息解答下列问题：
成绩等级频数分布表

成绩等级

频数

A

24

B

10

C

x

D

2

合计

y

成绩等级扇形统计图

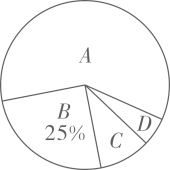(1)、x= ， y= ，扇形图中表示 $C$ 的圆心角的度数为度；

(2)、甲、乙、丙是 $A$ 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率.

查看试题解析

等级	非常了解	比较了解	基本了解	不太了解
人数（人）	24	72	18	$x$

次数	1	2	3	4	5	6
人数	1	2	a	6	b	2

成绩等级	频数
A	24
B	10
C	x
D	2
合计	y