广东省历年(2019-2023年)中考数学真题分类汇编12 相似
试卷更新日期:2023-08-06 类型:二轮复习
一、选择题
-
1. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数2. 在正方形 中, ,点E是 边的中点,连接 ,延长 至点F , 使得 ,过点F作 ,分别交 、 于N、G两点,连接 、 、 ,下列正确的是( )
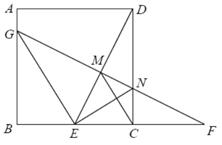
① ; ② ; ③ ; ④ .
A、4 B、3 C、2 D、13. 已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论: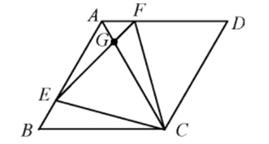
①△BCE≌△ACF②△CEF为正三角形③∠AGE=∠BEC④若AF=1,则EG=3FG正确的有( )个.
A、1 B、2 C、3 D、44. 如图,平行四边形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是( )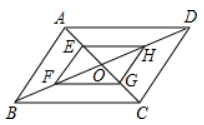 A、EH=HG B、四边形EFGH是平行四边形 C、AC⊥BD D、 的面积是 的面积的2倍5. 在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 ,则点A的坐标为( )A、 B、 C、 D、6. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( )
A、EH=HG B、四边形EFGH是平行四边形 C、AC⊥BD D、 的面积是 的面积的2倍5. 在平面直角坐标系xOy中,矩形OABC的点A在函数 的图象上,点C在函数 的图象上,若点B的横坐标为 ,则点A的坐标为( )A、 B、 C、 D、6. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、7. 如图,正方形 的边长为4,延长 至 使 ,以 为边在上方作正方形 ,延长 交 于 ,连接 、 , 为 的中点,连接 分别与 、 交于点 、 .则下列结论:① ;② ;③ ;④ .其中符合题意的结论有( )
A、 B、 C、 D、7. 如图,正方形 的边长为4,延长 至 使 ,以 为边在上方作正方形 ,延长 交 于 ,连接 、 , 为 的中点,连接 分别与 、 交于点 、 .则下列结论:① ;② ;③ ;④ .其中符合题意的结论有( )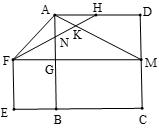 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
8. 边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 .
 9. 如图,已知四边形ABCD,AC与BD相交于点O,∠ABC=∠DAC=90°, ,则 = .
9. 如图,已知四边形ABCD,AC与BD相交于点O,∠ABC=∠DAC=90°, ,则 = .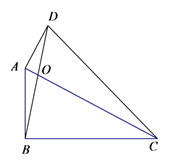 10. 如图,正方形 中, 绕点 逆时针旋转到 , , 分别交对角线 于点 ,若 ,则 的值为 .
10. 如图,正方形 中, 绕点 逆时针旋转到 , , 分别交对角线 于点 ,若 ,则 的值为 .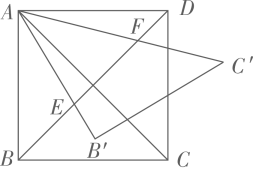 11. 如图,在中, , , 点D为上一动点,连接 , 将沿翻折得到 , 交于点G, , 且 , 则 .
11. 如图,在中, , , 点D为上一动点,连接 , 将沿翻折得到 , 交于点G, , 且 , 则 .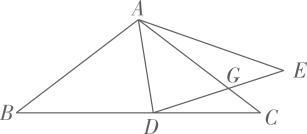 12. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 ,以点A为圆心,3为半径的圆分别交AB、AD于点F、G , DF与AE交于点H . 并与 交于点K , 连结HG、CH . 给出下列四个结论.(1)H是FK的中点;(2) ;(3) ;(4) ,其中正确的结论有(填写所有符合题意结论的序号).
12. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 ,以点A为圆心,3为半径的圆分别交AB、AD于点F、G , DF与AE交于点H . 并与 交于点K , 连结HG、CH . 给出下列四个结论.(1)H是FK的中点;(2) ;(3) ;(4) ,其中正确的结论有(填写所有符合题意结论的序号).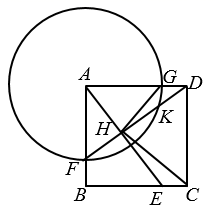
三、解答题
-
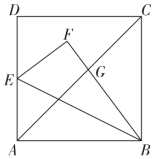
13. 如图,边长为1的正方形 中,点E为 的中点.连接 ,将 沿 折叠得到 交 于点G , 求 的长.
四、综合题
-
14. 如图,在单位长度为1的网格中,点O,A,B均在格点上, , , 以O为圆心,为半径画圆,请按下列步骤完成作图,并回答问题:
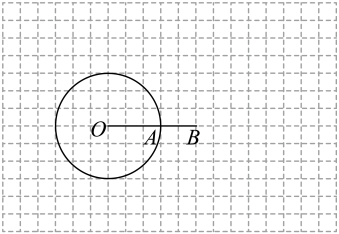
①过点A作切线 , 且(点C在A的上方);
②连接 , 交于点D;
③连接 , 与交于点E.
(1)、求证:为的切线;(2)、求的长度.15. 如图, 为 的弦,D , C为 的三等分点, .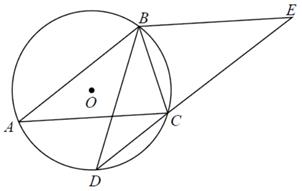 (1)、求证: ;(2)、若 , ,求 的长.16. 背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.小组讨论后,提出了三个问题,请你帮助解答:
(1)、求证: ;(2)、若 , ,求 的长.16. 背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.小组讨论后,提出了三个问题,请你帮助解答: (1)、将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如若不能,请说明理由:(2)、把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)、把背景中的正方形改成矩形AEFG和矩形ABCD,且 ,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值.17. 如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , .
(1)、将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如若不能,请说明理由:(2)、把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)、把背景中的正方形改成矩形AEFG和矩形ABCD,且 ,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值.17. 如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧, ,过点 的直线与 轴正半轴和抛物线的交点分别为 , , . (1)、求 , 的值;(2)、求直线 的函数解析式;(3)、点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写出所有满足条件的点 的坐标.18. 如图1,在四边形 中, , , 是 的直径, 平分 .
(1)、求 , 的值;(2)、求直线 的函数解析式;(3)、点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写出所有满足条件的点 的坐标.18. 如图1,在四边形 中, , , 是 的直径, 平分 .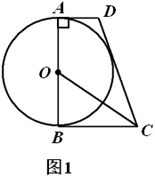 (1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.
(1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.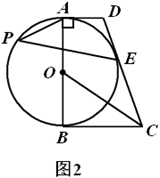 19. 如图,在 中,点 是边 上的一点.
19. 如图,在 中,点 是边 上的一点.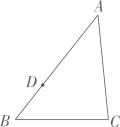 (1)、请用尺规作图法,在 内,求作 ,使 , 交 于 ;(不要求写作法,保留作图痕迹)(2)、在(1)的条件下,若 ,求 的值.20. 如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数 的图像相交于A,P两点。
(1)、请用尺规作图法,在 内,求作 ,使 , 交 于 ;(不要求写作法,保留作图痕迹)(2)、在(1)的条件下,若 ,求 的值.20. 如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数 的图像相交于A,P两点。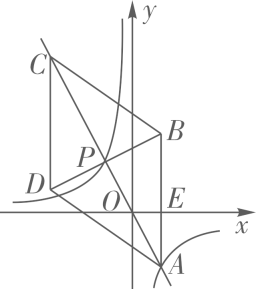 (1)、求m,n的值与点A的坐标;(2)、求证: ∽(3)、求 的值21. 综合运用
(1)、求m,n的值与点A的坐标;(2)、求证: ∽(3)、求 的值21. 综合运用如图1,在平面直角坐标系中,正方形的顶点A在轴的正半轴上,如图2,将正方形绕点逆时针旋转,旋转角为 , 交直线于点 , 交轴于点 .
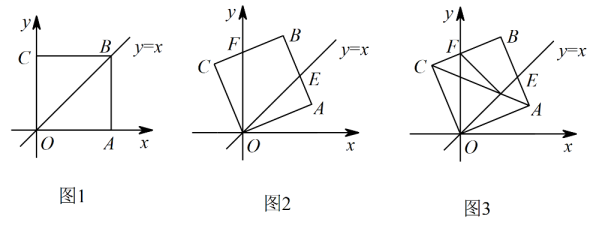 (1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.22. 如图,在菱形ABCD中, , ,点E为边AB上一个动点,延长BA到点F , 使 ,且CF、DE相交于点G
(1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.22. 如图,在菱形ABCD中, , ,点E为边AB上一个动点,延长BA到点F , 使 ,且CF、DE相交于点G (1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当 时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.23. 在平面直角坐标系 中,一次函数 的图象与x轴、y轴分别交于A、B两点,且与反比例函数 图象的一个交点为 .(1)、求m的值;(2)、若 ,求k的值.24. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.
(1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当 时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.23. 在平面直角坐标系 中,一次函数 的图象与x轴、y轴分别交于A、B两点,且与反比例函数 图象的一个交点为 .(1)、求m的值;(2)、若 ,求k的值.24. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.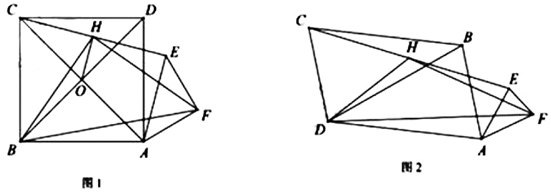 (1)、① ▲ ;
(1)、① ▲ ;② ▲ .
③小明为了证明①②,连接 交 于O , 连接 ,证明了 和 的关系,请你按他的思路证明①②.
(2)、小明又用三个相似三角形(两个大三角形全等)摆出如图2, , ( )求① (用k的代数式表示)
② (用k、 的代数式表示)
25. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?同学们有以下思路:
①设新矩形长和宽为x、y , 则依题意 , ,
联立 得 ,再探究根的情况:
根据此方法,请你探究是否存在一个矩形,使其周长和面积都为原矩形的 倍;
②如图也可用反比例函数与一次函数证明 : , : ,那么,
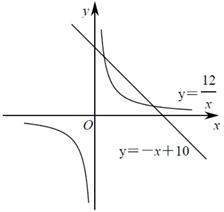
a . 是否存在一个新矩形为原矩形周长和面积的2倍?
b . 请探究是否有一新矩形周长和面积为原矩形的 ,若存在,用图像表达;
c . 请直接写出当结论成立时k的取值范围:.
26. 如图,点 是反比例函数 ( )图象上一点,过点 分别向坐标轴作垂线,垂足为 , ,反比例函数 ( )的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .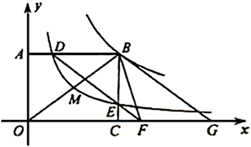 (1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.27. 已知在平面直角坐标系中,点A(3,0),B(-3,0),C(-3,8),以线段BC为直径作圆,圆心为E,直线AC交□E于点D,连接OD.
(1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.27. 已知在平面直角坐标系中,点A(3,0),B(-3,0),C(-3,8),以线段BC为直径作圆,圆心为E,直线AC交□E于点D,连接OD.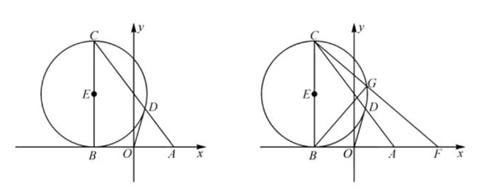 (1)、求证:直线OD是□E的切线;(2)、点F为x轴上任意一点,连接CF交□E于点G,连接BG:
(1)、求证:直线OD是□E的切线;(2)、点F为x轴上任意一点,连接CF交□E于点G,连接BG:当tan∠FCA= ,求所有F点的坐标(直接写出);
28. 如图,等边 中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合), 关于DE的轴对称图形为 . (1)、当点F在AC上时,求证:DF//AB;(2)、设 的面积为S1 , 的面积为S2 , 记S=S1-S2 , S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;(3)、当B,F,E三点共线时。求AE的长。
(1)、当点F在AC上时,求证:DF//AB;(2)、设 的面积为S1 , 的面积为S2 , 记S=S1-S2 , S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;(3)、当B,F,E三点共线时。求AE的长。
-