广东省历年(2019-2023年)中考数学真题分类汇编10 圆
试卷更新日期:2023-08-06 类型:二轮复习
一、选择题
-
1. 如图,是的直径, , 则( )
 A、 B、 C、 D、2. 一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若 ,则劣弧AB的长是( )
A、 B、 C、 D、2. 一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若 ,则劣弧AB的长是( )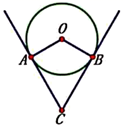 A、 B、 C、 D、3. 如图, 是⊙O的直径,点C为圆上一点, 的平分线交 于点D , ,则⊙O的直径为( )
A、 B、 C、 D、3. 如图, 是⊙O的直径,点C为圆上一点, 的平分线交 于点D , ,则⊙O的直径为( ) A、 B、 C、1 D、24. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、分式方程 的解为x=2 D、三角形的一个外角等于两个内角的和5. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )
A、 B、 C、1 D、24. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、分式方程 的解为x=2 D、三角形的一个外角等于两个内角的和5. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )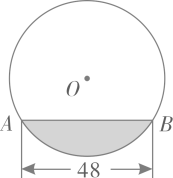 A、 B、 C、 D、6. 平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线条数为( )A、0条 B、1条 C、2条 D、无数条7. 设O为坐标原点,点A、B为抛物线 上的两个动点,且 .连接点A、B , 过O作 于点C , 则点C到y轴距离的最大值( )A、 B、 C、 D、1
A、 B、 C、 D、6. 平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线条数为( )A、0条 B、1条 C、2条 D、无数条7. 设O为坐标原点,点A、B为抛物线 上的两个动点,且 .连接点A、B , 过O作 于点C , 则点C到y轴距离的最大值( )A、 B、 C、 D、1二、填空题
-
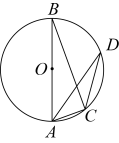
8. 如图,在中,为直径,C为圆上一点,的角平分线与交于点D,若 , 则°.
 9. 同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是 .10. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则∠E=。
9. 同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是 .10. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则∠E=。 11. 如图,等腰直角三角形 中, .分别以点B、点C为圆心,线段 长的一半为半径作圆弧,交 、 、 于点D、E、F , 则图中阴影部分的面积为 .
11. 如图,等腰直角三角形 中, .分别以点B、点C为圆心,线段 长的一半为半径作圆弧,交 、 、 于点D、E、F , 则图中阴影部分的面积为 . 12. 如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 .
12. 如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为 .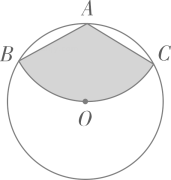 13. 如图,在平行四边形ABCD中,AB<AD,∠C=150°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为 .
13. 如图,在平行四边形ABCD中,AB<AD,∠C=150°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为 .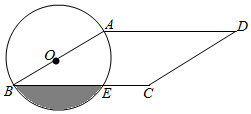
三、综合题
-
14. 如图,在单位长度为1的网格中,点O,A,B均在格点上, , , 以O为圆心,为半径画圆,请按下列步骤完成作图,并回答问题:
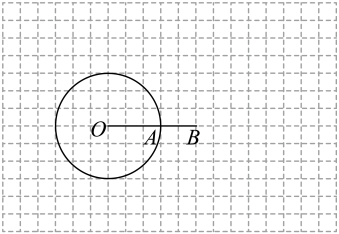
①过点A作切线 , 且(点C在A的上方);
②连接 , 交于点D;
③连接 , 与交于点E.
(1)、求证:为的切线;(2)、求的长度.15. 如图, 为 的弦,D , C为 的三等分点, .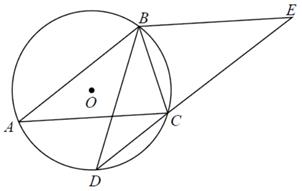 (1)、求证: ;(2)、若 , ,求 的长.16. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)、求证: ;(2)、若 , ,求 的长.16. 如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E. (1)、求证:AE=AB;(2)、若AB=10,BC=6,求CD的长.17. 如图, 为等边 的外接圆,半径为2,点 在劣弧 上运动(不与点 重合),连接 , , .
(1)、求证:AE=AB;(2)、若AB=10,BC=6,求CD的长.17. 如图, 为等边 的外接圆,半径为2,点 在劣弧 上运动(不与点 重合),连接 , , .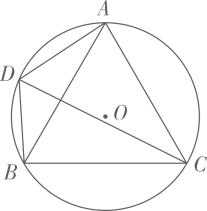 (1)、求证: 是 的平分线;(2)、四边形 的面积 是线段 的长 的函数吗?如果是,求出函数解析式;如果不是,请说明理由;(3)、若点 分别在线段 , 上运动(不含端点),经过探究发现,点 运动到每一个确定的位置, 的周长有最小值 ,随着点 的运动, 的值会发生变化,求所有 值中的最大值.18. 如图1,在四边形 中, , , 是 的直径, 平分 .
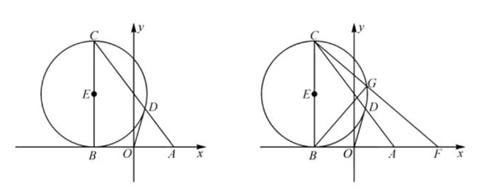
(1)、求证: 是 的平分线;(2)、四边形 的面积 是线段 的长 的函数吗?如果是,求出函数解析式;如果不是,请说明理由;(3)、若点 分别在线段 , 上运动(不含端点),经过探究发现,点 运动到每一个确定的位置, 的周长有最小值 ,随着点 的运动, 的值会发生变化,求所有 值中的最大值.18. 如图1,在四边形 中, , , 是 的直径, 平分 .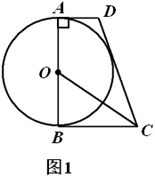 (1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.
(1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.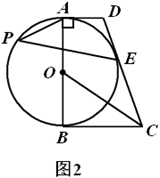 19. 如图1,在 中, , 是 的外接圆,过点 作 交 于点 ,连接 交 于点 ,延长 至点 ,使 ,连接 .
19. 如图1,在 中, , 是 的外接圆,过点 作 交 于点 ,连接 交 于点 ,延长 至点 ,使 ,连接 .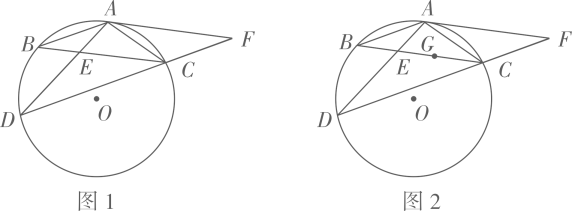 (1)、求证: ;(2)、求证: 是 的切线;(3)、如图2,若点 是 的内心, ,求 的长.20. 在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点, 的三个顶点均在格点上,以点 为圆心的 与 相切于点 ,分别交 、 于点 、 .
(1)、求证: ;(2)、求证: 是 的切线;(3)、如图2,若点 是 的内心, ,求 的长.20. 在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点, 的三个顶点均在格点上,以点 为圆心的 与 相切于点 ,分别交 、 于点 、 .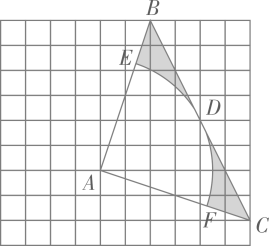 (1)、求 三边的长;(2)、求图中由线段 、 、 及 所围成的阴影部分的面积.
(1)、求 三边的长;(2)、求图中由线段 、 、 及 所围成的阴影部分的面积.