广东省历年(2019-2023年)中考数学真题分类汇编9 四边形
试卷更新日期:2023-08-06 类型:二轮复习
一、选择题
-
1. 如图,在平行四边形中, , , 将线段水平向右平移a个单位长度得到线段 , 若四边形为菱形时,则a的值为( )
 A、1 B、2 C、3 D、42. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判定四边形ABCD是平行四边形的是( )
A、1 B、2 C、3 D、42. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判定四边形ABCD是平行四边形的是( ) A、AB∥DC,AD∥BC B、AB= DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OB=OD3. 在 中,若 , ,则 的周长是( )A、15 B、16 C、18 D、204. 如图,抛物线经过正方形的三个顶点A,B,C,点B在轴上,则的值为( )
A、AB∥DC,AD∥BC B、AB= DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OB=OD3. 在 中,若 , ,则 的周长是( )A、15 B、16 C、18 D、204. 如图,抛物线经过正方形的三个顶点A,B,C,点B在轴上,则的值为( ) A、 B、 C、 D、5. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、分式方程 的解为x=2 D、三角形的一个外角等于两个内角的和6. 中,点 分别是 的边 , 的中点,连接 ,若 ,则 ( )A、 B、 C、 D、7. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、78. 已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为( )A、8 B、 C、16 D、49. 下面命题正确的是( )A、矩形对角线互相垂直 B、方程x2=14x的解为x=14 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等10. 已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论:
A、 B、 C、 D、5. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、分式方程 的解为x=2 D、三角形的一个外角等于两个内角的和6. 中,点 分别是 的边 , 的中点,连接 ,若 ,则 ( )A、 B、 C、 D、7. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、78. 已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为( )A、8 B、 C、16 D、49. 下面命题正确的是( )A、矩形对角线互相垂直 B、方程x2=14x的解为x=14 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等10. 已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论: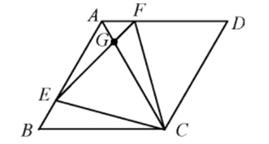
①△BCE≌△ACF②△CEF为正三角形③∠AGE=∠BEC④若AF=1,则EG=3FG正确的有( )个.
A、1 B、2 C、3 D、411. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
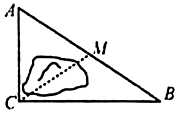
12. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AB的长为10km,则M,C之间的距离是km.
 13. 边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 .
13. 边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 . 14. 已知菱形的两条对角线长分别为6和8,则它的面积为 .15. 如图,在 中, .过点D作 ,垂足为E , 则 .
14. 已知菱形的两条对角线长分别为6和8,则它的面积为 .15. 如图,在 中, .过点D作 ,垂足为E , 则 .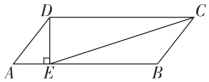 16. 如图,在 中,D , E分别为 , 上的点,将 沿 折叠,得到 ,连接 , , ,若 , , ,则 的长为.
16. 如图,在 中,D , E分别为 , 上的点,将 沿 折叠,得到 ,连接 , , ,若 , , ,则 的长为.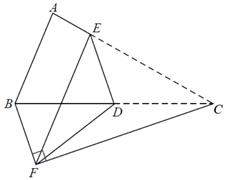 17. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= .
17. 如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数 的图象经过▱OABC的顶点C,则k= . 18. 如图,点 的坐标为 ,点 在 轴上,把 沿 轴向右平移到 ,若四边形 的面积为9,则点 的坐标为 .
18. 如图,点 的坐标为 ,点 在 轴上,把 沿 轴向右平移到 ,若四边形 的面积为9,则点 的坐标为 .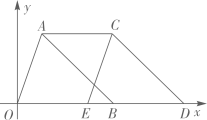 19. 如图,正方形 中, 绕点 逆时针旋转到 , , 分别交对角线 于点 ,若 ,则 的值为 .
19. 如图,正方形 中, 绕点 逆时针旋转到 , , 分别交对角线 于点 ,若 ,则 的值为 .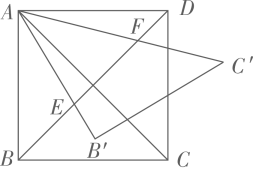 20. 如图,在正方形ABCD中,BE=1,将BC沿CE翻折,使B点对应点刚好落在对角线AC上,将AD沿AF翻折,使D点对应点刚好落在对角线AC上,求EF= .
20. 如图,在正方形ABCD中,BE=1,将BC沿CE翻折,使B点对应点刚好落在对角线AC上,将AD沿AF翻折,使D点对应点刚好落在对角线AC上,求EF= . 21. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 ,以点A为圆心,3为半径的圆分别交AB、AD于点F、G , DF与AE交于点H . 并与 交于点K , 连结HG、CH . 给出下列四个结论.(1)H是FK的中点;(2) ;(3) ;(4) ,其中正确的结论有(填写所有符合题意结论的序号).
21. 如图,正方形ABCD的边长为4,点E是边BC上一点,且 ,以点A为圆心,3为半径的圆分别交AB、AD于点F、G , DF与AE交于点H . 并与 交于点K , 连结HG、CH . 给出下列四个结论.(1)H是FK的中点;(2) ;(3) ;(4) ,其中正确的结论有(填写所有符合题意结论的序号).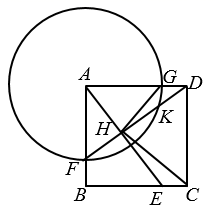
三、作图题
-
22. 如图,在中, .
 (1)、实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)(2)、应用与计算:在(1)的条件下, , , 求的长.23. 如图, 中, .(1)、作点 关于 的对称点 ;(要求:尺规作图,不写作法,保留作图痕迹)
(1)、实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)(2)、应用与计算:在(1)的条件下, , , 求的长.23. 如图, 中, .(1)、作点 关于 的对称点 ;(要求:尺规作图,不写作法,保留作图痕迹)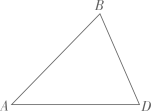 (2)、在(1)所作的图中,连接 , ,连接 ,交 于点 .
(2)、在(1)所作的图中,连接 , ,连接 ,交 于点 .①求证:四边形 是菱形;
②取 的中点 ,连接 ,若 , ,求点 到 的距离.
四、解答题
-
24. 如图,在平行四边形ABCD中,E,F分别是AB,CD边上的点,且AE=CF,求证:四边形EBFD是平行四边形.

五、综合题
-
25. 如图,在四边形 中, ,点E、F分别在线段 、 上,且 .
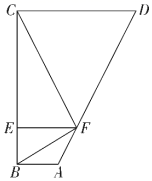 (1)、求证: ;(2)、求证:以 为直径的圆与 相切;(3)、若 ,求 的面积.26. 如图,⊙O的直径AB=10,弦AC=8,连接BC。
(1)、求证: ;(2)、求证:以 为直径的圆与 相切;(3)、若 ,求 的面积.26. 如图,⊙O的直径AB=10,弦AC=8,连接BC。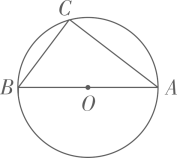 (1)、尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)(2)、在(1)所作的图中,求四边形ABCD的周长。27.(1)、如图,在矩形中,为边上一点,连接 ,
(1)、尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)(2)、在(1)所作的图中,求四边形ABCD的周长。27.(1)、如图,在矩形中,为边上一点,连接 ,①若 , 过作交于点 , 求证:;
②若时,则 .
 (2)、如图,在菱形中, , 过作交的延长线于点 , 过作交于点 , 若时,求的值.
(2)、如图,在菱形中, , 过作交的延长线于点 , 过作交于点 , 若时,求的值. (3)、如图,在平行四边形中, , , , 点在上,且 , 点为上一点,连接 , 过作交平行四边形的边于点 , 若时,请直接写出的长.
(3)、如图,在平行四边形中, , , , 点在上,且 , 点为上一点,连接 , 过作交平行四边形的边于点 , 若时,请直接写出的长. 28. 综合运用
28. 综合运用如图1,在平面直角坐标系中,正方形的顶点A在轴的正半轴上,如图2,将正方形绕点逆时针旋转,旋转角为 , 交直线于点 , 交轴于点 .
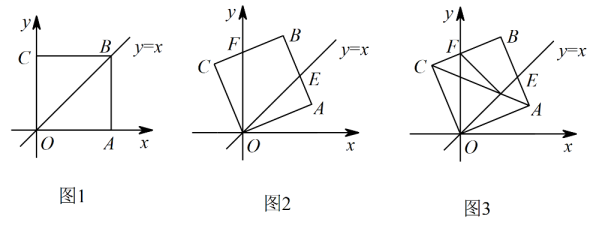 (1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.29. 如图,矩形的顶点A,C分别落在x轴,y轴的正半轴上,顶点 , 反比例函数的图象与 , 分别交于D,E, .
(1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.29. 如图,矩形的顶点A,C分别落在x轴,y轴的正半轴上,顶点 , 反比例函数的图象与 , 分别交于D,E, . (1)、求反比例函数关系式和点E的坐标;(2)、写出与的位置关系并说明理由;(3)、点F在直线上,点G是坐标系内点,当四边形为菱形时,求出点G的坐标.30. 如图,在菱形ABCD中, , ,点E为边AB上一个动点,延长BA到点F , 使 ,且CF、DE相交于点G
(1)、求反比例函数关系式和点E的坐标;(2)、写出与的位置关系并说明理由;(3)、点F在直线上,点G是坐标系内点,当四边形为菱形时,求出点G的坐标.30. 如图,在菱形ABCD中, , ,点E为边AB上一个动点,延长BA到点F , 使 ,且CF、DE相交于点G (1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当 时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.31. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.
(1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当 时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.31. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.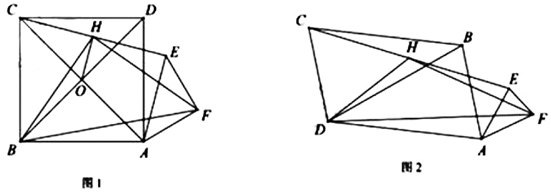 (1)、① ▲ ;
(1)、① ▲ ;② ▲ .
③小明为了证明①②,连接 交 于O , 连接 ,证明了 和 的关系,请你按他的思路证明①②.
(2)、小明又用三个相似三角形(两个大三角形全等)摆出如图2, , ( )求① (用k的代数式表示)
② (用k、 的代数式表示)
32. 如图,点 是反比例函数 ( )图象上一点,过点 分别向坐标轴作垂线,垂足为 , ,反比例函数 ( )的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .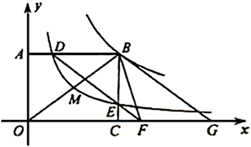 (1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.33. 如图1,在平面直角坐标系中,抛物线 与 轴交于点 、 (点 在点 右侧),点 为抛物线的顶点.点 在 轴的正半轴上, 交 轴于点 , 绕点 顺时针旋转得到 ,点 恰好旋转到点 ,连接 .
(1)、填空: ;(2)、求 的面积;(3)、求证:四边形 为平行四边形.33. 如图1,在平面直角坐标系中,抛物线 与 轴交于点 、 (点 在点 右侧),点 为抛物线的顶点.点 在 轴的正半轴上, 交 轴于点 , 绕点 顺时针旋转得到 ,点 恰好旋转到点 ,连接 .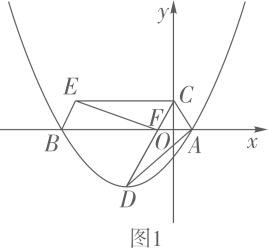
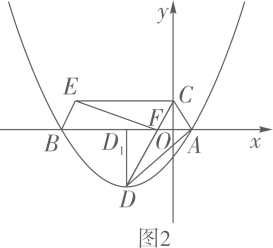 (1)、求点 、 、 的坐标;(2)、求证:四边形 是平行四边形;(3)、如图2,过顶点 作 轴于点 ,点 是抛物线上一动点,过点 作 轴,点 为垂足,使得 与 相似(不含全等).
(1)、求点 、 、 的坐标;(2)、求证:四边形 是平行四边形;(3)、如图2,过顶点 作 轴于点 ,点 是抛物线上一动点,过点 作 轴,点 为垂足,使得 与 相似(不含全等).①求出一个满足以上条件的点 的横坐标;
②直接回答这样的点 共有几个?
-